《高等数学》课程教学资源（PPT课件）8.1向量及其线形运算

第章 句量代数与空间解折儿何 第一部分向量代数 第二部分空间解析几何 在三维空间中： 空间形式一 点，线，面 T 数量关系 坐标，方程（组) 基本方法 一坐标法：向量法

数量关系 — 第八章 第一部分 向量代数 第二部分 空间解析几何 在三维空间中: 空间形式 — 点, 线, 面 基本方法 — 坐标法; 向量法 坐标, 方程（组） 向量代数与空间解析几何

第一节 第八章 句量及其线性运算 一、向量的概念 二 、向量的线性运算 三、空间直角坐标系 四、利用坐标作向量的线性运算 五、向量的模、方向角、投影 HIGH EDUCATION PRESS 机动目 页返回结束

四、利用坐标作向量的线性运算 第一节 一、向量的概念 二、向量的线性运算 三、空间直角坐标系 五、向量的模、方向角、投影 机动 目录 上页 下页 返回 结束 向量及其线性运算 第八章

一、向量的概念 向量：既有大小，又有方向的量称为向量（又称矢量） 表示法有向线段M2,或a,或a 向量的模：向量的大小，记作MM2,或a,或a 向径（矢径）：起点为原点的向量 自由向量：与起点无关的向量 单位向量：模为1的向量，记作或a°. 零向量：模为0的向量，记作0，或0 HIGH EDUCATION PRESS DeOC8 机动目录上页下页返回结束

表示法: 向量的模 : 向量的大小, 一、向量的概念 向量: (又称矢量). M1 M2 既有大小, 又有方向的量称为向量 向径 (矢径): 自由向量: 与起点无关的向量. 起点为原点的向量. 单位向量: 模为 1 的向量, 零向量: 模为 0 的向量, 有向线段 M1 M2 , 或 a , 机动 目录 上页 下页 返回 结束

若向量ā与b大小相等，方向相同，则称ā与b相等 记作a=b; 若向量ā与五方向相同或相反，则称ā与平行，记作 ā/b；规定：零向量与任何向量平行， 与ā的模相同，但方向相反的向量称为ā的负向量， 记作-a; 因平行向量可平移到同一直线上，故两向量平行又称 两向量共线 若k仑3)个向量经平移可移到同一平面上，则称此k 个向量共面 等HIGH EDUCATION PRESS 机动目 下页返回结束

规定: 零向量与任何向量平行 ; 若向量 a 与 b大小相等, 方向相同, 则称 a 与 b 相等, 记作 a＝b ; 若向量 a 与 b 方向相同或相反, 则称 a 与 b 平行, a∥b ; 与 a 的模相同, 但方向相反的向量称为 a 的负向量, 记作 因平行向量可平移到同一直线上, 故两向量平行又称 两向量共线 . 若 k (≥3)个向量经平移可移到同一平面上 , 则称此 k 个向量共面 . 记作－a ; 机动 目录 上页 下页 返回 结束

二、向量的线性运算 1.向量的加法 平行四边形法则： (@+B)+c a+币 b+c a+(B+c) a+不 三角形法则： a+b a a 运算规律：交换律 a+b-b+a 结合律 (a+b)+c-a+(b+c)-a+B+c 三角形法则可推广到多个向量相加 HIGH EDUCATION PRESS 机动目录上页下页返回结束

二、向量的线性运算 1. 向量的加法 三角形法则: 平行四边形法则: 运算规律 : 交换律 结合律 三角形法则可推广到多个向量相加 . 机动 目录 上页 下页 返回 结束 b b a + b = b + a (a + b) + c = a + (b + c ) = a + b + c a b c a + b b + c a + (b + c ) (a + b) + c a a a + b a + b

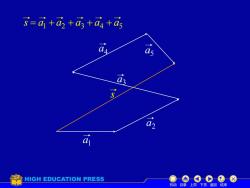
s=a +a +as+as +as 05 HIGH EDUCATION PRESS 机动目录上页下页返回结束

机动 目录 上页 下页 返回 结束 s a3 a4 a5 a2 a1 a1 a2 a3 a4 a5 s = + + + +

2.向量的减法 b-a=b+(-) 6-a b-a 特别当b=a时，有 a-a-a+(-a)-0 a 三角不等式 a+b s a+B a-b s a+b HIGH EDUCATION PRESS 机动目录上页下页返回结束

2. 向量的减法 三角不等式 机动 目录 上页 下页 返回 结束 a

3.向量与数的乘法 )是一个数，)与a的乘积是一个新向量，记作a. 规定：2>0时，2a与a同向，2a=2a; 2<0时，a与a反向，2a=-a； 2=0时，2a=0 总之 |2a=2|a 运算律：结合律(uad)=4(2a)=2uā 分配律 (2+a=2a+ud (ā+b)=元a+2b 若a#0,则有单位向量日=日a 因此a=aa HIGH EDUCATION PRESS 机动目录上页下页返回结束

a a    =  3. 向量与数的乘法  是一个数 , a .   规定 : 1a a ;   = 可见 1a a ;   − = −  与 a 的乘积是一个新向量, 记作 总之: 运算律 : 结合律 ( a)    ( a)  =   a  =   分配律 (a b)    + a b   =  +  =  则有单位向量 a . 1 a a   因此    a = a a 机动 目录 上页 下页 返回 结束

定理1.设a为非零向量，则 a/b三b=2a ()为唯一实数) 证“一设a/6,取=士/石，a,万同向时 取正号，反向时取负号，则与入a同向，且 -2-骨。 故b=na 再证数入的唯一性.设又有=4a,则(2-0)a=可 而a≠0，故2-4=0，即=4 HIGH EDUCATION PRESS 机动目录上页下页返回结束

定理1. 设 a 为非零向量 , 则 ( 为唯一实数) 证: “ ”. , 取 ＝± 且 再证数  的唯一性 . 则 故  −  = 0, 即 =  . a∥b 设 a∥b 取正号, 反向时取负号, , a , b 同向时 则 b 与  a 同向, 设又有 b＝ a , ( − )a = 0 = = b 故 b =  a. 机动 目录 上页 下页 返回 结束

一”已知b=a,则 当2=0时，b=可 当2>0时，a,b同向 allb 当2<0时，a,b反向 例1.设M为□ABCD对角线的交点，AB=d,AD=b, 试用a与b表示MA,MB,MC,MD 解：a+b=AC=2MC=-2MA b-a=BD=2MD=-2MB M=-(a+bM丽=-6-a) MC=j(a+B) MD=j(b-a) HIGH EDUCATION PRESS 机动目录上页下页返回结束

“ ” 则 例1. 设 M 为 M A B 解: D C ABCD 对角线的交点, b a AC = −2MA BD = −2MB 已知 b＝ a , b＝0 a , b 同向 a , b 反向 a∥b 试用a 与b 表示 MA,MB,MC,MD. a + b = b − a = ( ) 2 1  MA = − a + b ( ) 2 1 MB = − b − a ( ) 2 1 MC = a + b ( ) 2 1 MD = b − a 机动 目录 上页 下页 返回 结束