《线性代数》课程教学课件（PPT讲稿，B）第三章 矩阵的运算 §3.3 初等矩阵

第三章矩阵的运算 §3.3初等矩阵 初等矩阵的概念 二、 初等矩阵的应用 三、小结思考题

第三章 矩阵的运算 三、小结 思考题 二、初等矩阵的应用 一、初等矩阵的概念 §3.3 初等矩阵

第三章矩阵的运算 一、初等矩阵的概念 矩阵的初等变换是矩阵的一种基本运算，应 用广泛 定义3.3.1由单位矩阵E经过一次初等变换得到的 方阵称为初等矩阵， 三种初等变换对应着三种初等方阵。 1.对调两行或两列； 2.以数k≠0乘某行或某列； 3.以数k乘某行（列）加到另一行（列）上去

第三章 矩阵的运算 定义3.3.1 由单位矩阵 E 经过一次初等变换得到的 方阵称为初等矩阵. 三种初等变换对应着三种初等方阵. 矩阵的初等变换是矩阵的一种基本运算，应 用广泛.       以数 乘某行（列）加到另一行（列）上去． 以数 乘某行或某列； 对调两行或两列； k k 3. 2. 0 1. 一、初等矩阵的概念

第三章矩阵的运算 1、对调两行或两列 对调E中第i,两行，即(，→r),得初等方阵 ←第i行 E(i,j)= ←第j行

第三章 矩阵的运算 对调 E 中第 i, j 两行，即(ri  rj )，得初等方阵 1、对调两行或两列 1 1 0 1 1 ( , ) 1 1 0 1 1 E i j     =    第 i 行  第 j 行

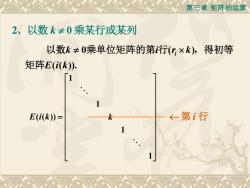
第三章矩阵的运算 2、以数k≠0乘某行或某列 以数k≠0乘单位矩阵的第行(y×k),得初等 矩阵E(i(k) [1 E(i(k)= ←-第i行

第三章 矩阵的运算 2 0 、以数 k  乘某行或某列 ( ( )). 0 ( ) E i k k i ri k 矩阵 以数  乘单位矩阵的第 行  ，得初等 1 1 ( ( )) 1 1 E i k k           =              第 i 行

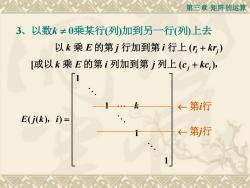
第三章矩阵的运算 3、以数k≠0乘某行（列加到另一行（列上去 以k乘E的第j行加到第i行上(+k灯) [或以k乘E的第i列加到第j列上(c+kc), ←第行 E(jk),)= ←第行

第三章 矩阵的运算 3 0 ( ) ( ) 、以数k  乘某行 列 加到另一行 列 上去 或以 乘 的第 列加到第 列上 ， 以 乘 的第 行加到第 行上 [ ( ) ( ) j i i j k E i j c kc k E j i r kr + + 1 1 ( ( ) ) 1 1 k E j k i           =             ，  第i行  第j行

第三章矩阵的运算 容易验证初等矩阵的逆矩阵仍然是同类的初等矩阵 E(i,)1=E(i,j); E(i)》1=E(i片 E(j(k),)-=E((-k),). 对矩阵进行初等变换，可以用相应的初等矩阵左乘 或右乘矩阵来表示

第三章 矩阵的运算 1 1 1 ( , ) ( , ); 1 ( ( )) ( ( )); ( ( ), ) ( ( ), ) . E i j E i j E i k E i k E j k i E j k i − − − = = = − 容易验证初等矩阵的逆矩阵仍然是同类的初等矩阵 对矩阵进行初等变换，可以用相应的初等矩阵左乘 或右乘矩阵来表示

第三章矩阵的运算 例如 12 。 1 2 Nin A= 。 2 (m2 。 C mn

第三章 矩阵的运算 11 12 1 1 2 1 2 1 2 n i i in j j jn m m mn a a a a a a A a a a a a a     =   例如

第三章矩阵的运算 用m阶初等矩阵E,m(亿，)左乘A,得 2 1 ←第i行 E (i,j)A= : ←-第j行 mn 相当于对矩阵A施行第一种初等行变换： 把A的第i行与第j行对调（分）

第三章 矩阵的运算 ( , ) 用m E i j A 阶初等矩阵 m 左乘 ，得 11 12 1 1 2 1 2 1 2 ( , ) n j j jn m i i in m m mn a a a a a a E i j A a a a a a a           =              第 i 行  第 j 行 ( ). i j A i j r r A 把 的第 行与第 行对调  相当于对矩阵 施行第一种初等行变换：

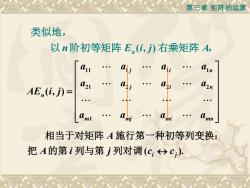
第三章矩阵的运算 类似地， 以n阶初等矩阵En(亿，)右乘矩阵A, AE,(i,j)= a21 m 相当于对矩阵A施行第一种初等列变换： 把A的第i列与第j列对调(c,)c)

第三章 矩阵的运算 ( , ) n E i j A n 类似地， 以 阶初等矩阵 右乘矩阵 ， 11 1 1 1 21 2 2 2 1 ( , ) j i n j i n n m mj mi mn a a a a a a a a AE i j a a a a       =         ( ). i j A i j c c A 把 的第 列与第 列对调  相当于对矩阵 施行第一种初等列变换：

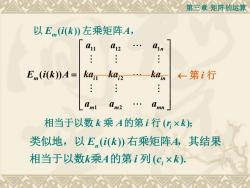
第三章矩阵的运算 以Em(i(k)左乘矩阵A, 1 12 n : E(i(kA= kc hdzhcim ←第i行 : : 相当于以数k乘A的第i行(U×k): 类似地，以E((k)右乘矩阵A,其结果 相当于以数k乘A的第i列(C,×k)

第三章 矩阵的运算 相当于以数 k 乘 A的第 i 行 (ri  k)； 11 12 1 1 2 1 2 ( ( )) n m i i in m m mn a a a E i k A ka ka ka a a a       =            第 i 行 ( ( )) ( ). n i E i k A k A i c k  类似地，以 右乘矩阵 ，其结果 相当于以数 乘 的第 列 以 Em (i(k))左乘矩阵A