《高等数学》课程教学资源（PPT课件）9.2偏导数

第九章 第二节 偏导数 偏导数概念及其计算 二、高阶偏导数 HIGH EDUCATION PRESS 机动目录上页下页返回结束

第二节 机动 目录 上页 下页 返回 结束 一、 偏导数概念及其计算 二 、高阶偏导数 偏 导 数 第九章

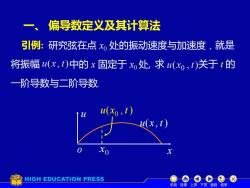
一、 偏导数定义及其计算法 引例：研究弦在点x处的振动速度与加速度，就是 将振幅u(x,t)中的x固定于xo处，求u(xo,t)关于1的 一阶导数与二阶导数 u(xo,1） u(x,t） HIGH EDUCATION PRESS 机动目录上页下页返回结束

一、 偏导数定义及其计算法 引例: 研究弦在点 x0 处的振动速度与加速度 , 就是 u(x, t) 0 o x x u 中的 x 固定于 求 一阶导数与二阶导数. x0 处, ( , ) 0 u x t 关于 t 的 机动 目录 上页 下页 返回 结束 将振幅

定义1.设函数z=f(x,y)在点(x0,yo)的某邻域内 极限 lim f(x+△x,0)-f(xo,y0) △x>0 △x 存在，则称此极限为函数：=f(x,y)在点(xo,o)对x 的偏导数，记为 of 0x(oo)》”0xx0yo)2xw) fx(xo,yo);(xo-yo). 注意：f(o,0)=1im= f(xo +Ax,yo)=f(xo,yo) △x→0 △x ,o) d HIGH EDUCATION PRESS 机动目录上页下页返回结束

定义1. z = f (x, y) 在点 存在, z f (x, y) 在点(x , y ) 对x = 0 0 的偏导数，记为 ( , ) 0 0 x y 的某邻域内 ; ( , ) 0 0 x x y f   x + x 0 0 x 则称此极限为函数 极限 设函数 f (x0 ) = ( ) ( ) 0 0 f x + x − f x x 0 lim x→ x ; ( , ) 0 0 x x y z d 0 d x x x y = = ( , ). 1 0 0 f  x y 机动 目录 上页 下页 返回 结束 x f x x y f x y x  +  − =  → ( , ) ( , ) lim 0 0 0 0 0 ( , ) 0 0 f x y 注意 x :

同样可定义对y的偏导数 f(o.0)lim f(o.)-f(o.Yo) △y>0 △y 若函数：=f(x,y)在域D内每一点(x,y)处对x 或y偏导数存在，则该偏导数称为偏导函数，也简称为 偏导数，记为 .,x,fc) Ox'Ox 0z ,f,川.，川 Oy'Oy HIGH EDUCATION PRESS 机动目录上页下页返回结束

同样可定义对 y 的偏导数 lim  →0 = y ( , ) 0 0 f x y y 若函数 z = f ( x , y ) 在域 D 内每一点 ( x , y ) 处对 x 则该偏导数称为偏导函数, 也简称为 偏导数 , ( , ) , ( , ) 2 f x y f x y y  ( , ) 0 f x ( , ) 0 − f x y 记为 y + y 0 0 y 机动 目录 上页 下页 返回 结束 或 y 偏导数存在 , , , , y z y f y z    

偏导数的概念可以推广到二元以上的函数 例如，三元函数u=f(x,y,)在点(x,y,)处对x的 偏导数定义为 (y2)lim (x+Ax)-f(x,y,=) △x->0 △x f(xy,)=? (请自己写出) f(x,y,z)=? HIGH EDUCATION PRESS ◆0C08 机动目录上页下页返回结束

例如, 三元函数 u = f (x , y , z) 在点 (x , y , z) 处对 x 的 偏导数的概念可以推广到二元以上的函数 . x x + x f (x, y,z) = ? y f (x, y,z) = ? z x 机动 目录 上页 下页 返回 结束 偏导数定义为 (请自己写出)

二元函数偏导数的几何意义： y=y 是曲线 在点场处的卷 y=Yo M,T,对x轴的斜率 y=Yo y=% 是曲线 2=(x,》在点M,处的切线MoI,对y轴的 X=X0 斜率 HIGH EDUCATION PRESS 机动目录上页下页返回结束

二元函数偏导数的几何意义: 0 0 ( , ) d d 0 0 x x f x y x x f x x y y = =   = =    = = 0 ( , ) y y z f x y M0Tx 0 0 ( , ) d d 0 0 y y f x y y y f x x y y = =   = = 是曲线 M0Ty 在点 M0 处的切线 对 x 轴的斜率. 在点M0 处的切线 斜率. 是曲线 y x z 0 x Ty o Tx 0 y M0 机动 目录 上页 下页 返回 结束 对 y 轴的

注意：函数在某点各偏导数都存在， 但在该点不一定连续 y≠0 例如，=fx,)= y2=0 显然Q0)-品x x=0=0 d (0.0)=f0.y)y=0=0 在上节已证f(x,y)在点(0,0)并不连续！ HIGH EDUCATION PRESS ○eC8 上节例目录上页下页返回结束

函数在某点各偏导数都存在, 显然 例如,      + = +  = = + 0 , 0 , 0 ( , ) 2 2 2 2 2 2 x y x y x y xy z f x y = 0 = 0 注意： 但在该点不一定连续. 上节例 目录 上页 下页 返回 结束 在上节已证 f (x , y) 在点(0 , 0)并不连续!

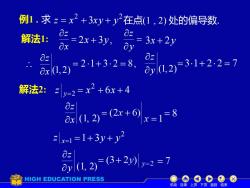
例1.求：=x2+3xy+y2在点(1,2)处的偏导数 解法1： 公2-y.x+2y 0z 02-21+3-2=8, 0z ⊙1,2)3.1+2.2=7 解法2 三y=2=x2+6x+4 品u3-a+0=18 2x=1=1+3y+y2 8328+2-7 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例1 . 求 2 2 z = x + 3xy + y 解法1: =   x z x (1,2) z    解法2: x (1, 2) z   在点(1 , 2) 处的偏导数. y (1, 2) z   2x + 3y , =   y z 3x + 2y y (1,2) z   6 4 2 = x + x + x=1 z 2 =1+ 3y + y y=2 z 机动 目录 上页 下页 返回 结束

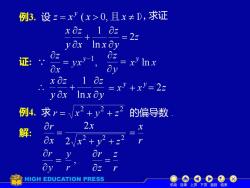
例3.设z=x'(x>0,且x≠D,求证 x02,10z =22 yox Inxay 0z 0z 证： Ox =x-1 8y x 0z 1 0z yOx Inxoy =xy+'=22 例4.求r=x2+y2+z2 的偏导数 解 Or 2x 8x 2Vx2+y2+2 Or 1 Or 0y 0z HIGH EDUCATION PRESS e0C①8 机动目录上页下页返回结束

例3. 设 z = x y ( x  0, 且 x 1）， z y z x x z y x 2 ln 1 =   +   证: y z x x z y x   +    ln 1 例4. 求 的偏导数 . 解: =   x r 求证 = 2z 2 2 2 2 x + y + z 2x r x = r z z r =   机动 目录 上页 下页 返回 结束

例5.已知理想气体的状态方程pV=RT(R为常数)， 求证 op av aT =-1 av RT RT 证： D= V v2 说明：此例表明， V= RT R 偏导数记号是一个 p 整体记号，不能看作 T- V 分子与分母的商！ R p R Op av RT =-1 av at op HIGH EDUCATION PRESS 机动目录上页下页返回结束

偏导数记号是一个 例5. 已知理想气体的状态方程 求证: = −1         p T T V V p 证: , V RT p = , p RT V = =          p T T V V p 说明: (R 为常数) , =   V p 2 V RT − =   T V p R pV RT − = −1 不能看作 分子与分母的商 ! 此例表明, 机动 目录 上页 下页 返回 结束 整体记号