《线性代数》课程教学课件（PPT讲稿，C）第四章 线性方程组 4-3 非齐次线性方程组

第四章线性方程组 §4.3非齐次线性方程组 非齐次线性方程组解的性质 非齐次线性方程组的通解

第四章 线性方程组 §4.3 非齐次线性方程组 一、非齐次线性方程组解的性质 二、非齐次线性方程组的通解

第四章线性方程组 一、 非齐次线性方程组解的性质 对于非齐次线性方程组(4-1) 411X1+012x2+.+41mXn=b, 2X1+022x2+.+2mXn=b2: (4-1) am+am2+amnxn=bm 1 L12 X1 6 记A= 421 a22 Q2n X2 ,b= b2 ,火= An An2 。● W Xn

第四章 线性方程组 一、非齐次线性方程组解的性质 对于非齐次线性方程组(4-1) 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 11 12 1 1 1 21 22 2 2 2 1 2 , . , , n n n n m m mn n m n n n n mn n m a x a x a x b a x a x a x b a x a x a x b a a a x b a a a x b A x b a a a x b                                                            ， 记 (4-1)

第四章线性方程组 则线性方程组(4-1)矩阵形式为A=b. 齐次线性方程组(4-5) 011x1+012x2+.+41nXn=0, 0211+022X2+.+2mXn=0, (4-5) ml七1+0m2七2+.+AmnXn=0. 可记为A=0. 我们把方程组(4-5)称为与方程组(4-1)对应的 齐次线性方程组或导出的齐次线性方程组

第四章 线性方程组 则线性方程组(4-1)矩阵形式为Ax=b. 齐次线性方程组(4-5) 11 1 12 2 1 21 1 22 2 2 1 1 2 2 0, 0 0. n n n n m m mn n a x a x a x a x a x a x a x a x a x                 ， 可记为Ax=0. 我们把方程组(4-5)称为与方程组(4-1)对应的 齐次线性方程组或导出的齐次线性方程组. (4-5)

第四章线性方程组 非齐次线性方程组(4-1)的解有下面性质： 性质4.3.1设x=n,及x=72是方程组(4-1)的解， 则k=7-7,是其对应的齐次方程组(4-5)的解， 证 .A71=b,A72=b .A(71-72)=b-b=0. 即x=71-72满足方程Ax=0

第四章 线性方程组 非齐次线性方程组(4-1)的解有下面性质: 1 2 1 2 4 (4 1) ( .3. 4 5) . 1 x x x           设 及 是方程组 的解， 则 是其对应的齐次方程组 性 的解 质 证   0.  A 1 2  b  b  0. 即x  1 2满足方程 Ax  A  b A  b 1 2   , 

第四章线性方程组 性质4.3.2设x=7是方程组(4-1)的解，x=5是方程组 (4-5)的解则x=n+5是方程组(4-1)的解， 证 Aξ+n)=A5+A7=0+b=b, 所以x=5+n是方程Ax=b的解

第四章 线性方程组 (4 1) (4 5) (4 1) . 4.3.2 x x x            设 是方程组 的解， 是方程组 的解则 是方程组 性 的解 质 证 A   A  A  0  b  b, 所以x    是方程 Ax  b的解

第四章线性方程组 二、非齐次线性方程组的通解 由性质4.3.1知，若已知(4-1)的一个解（特解）m*, 则(4-1)的任一解x总可以表示为 x=(x-n)+n=5+n (4-6) 其中5=x-1*为齐次方程组(4-5)的解 (4-6)式表明非齐次方程组(4-1)的任一解都可以表 示为它的一个特定解*与它的导出组一个解的和

第四章 线性方程组 二、非齐次线性方程组的通解 由性质4.3.1知,若已知(4-1)的一个解(特解)η* , 则(4-1)的任一解x总可以表示为 * * * x  (x  )     其中ξ = x - η*为齐次方程组(4-5)的解. (4-6) (4-6)式表明非齐次方程组(4-1)的任一解都可以表 示为它的一个特定解η*与它的导出组一个解的和

第四章线性方程组 反过来，由性质4.3.2可知，对任何数k1,k2,kn-, x=k151+k252+.+km-,5m-r+7 总是方程(4-1)的解.因此 方程组(4-1)的通解为 x=k151+k252+.+km-,5m-,+7 其中51,52.，5n-,是(4-5)式的基础解系， k1,k2,km,为任意数

第四章 线性方程组 反过来,由性质4.3.2可知,对任何数 总是方程(4-1)的解. 因此 1 2 , , , n r k k k   * 1 1 2 2 n r n r x  k   k     k     1 2 , , , n r k k k   * 1 1 2 2 n r n r x  k   k     k      1 2 , , , n r    其中   是(4-5)式的基础解系, 为任意数. 方程组(4-1)的通解为

第四章线性方程组 例1求解方程组 1+X2-3x3-4=1, 3x1-x2-3x3+4x4=4, x1+5x2-9x3-8x4=0. 解对增广矩阵进行初等行变换化成行最简形 Γ11-3-11-3r「113-1 1 A=3-1-3 44 0-4 6 71 15-9803-1046 -7-1

第四章 线性方程组 1 2 3 4 1 2 3 4 1 2 3 4 3 1, 3 3 4 4, 5 9 8 0. x x x x x x x x x x x x                  例1 求解方程组 1 1 3 1 1 3 1 3 4 4 1 5 9 8 0 A              2 1 3 1 3 1 1 3 1 1 ~ 0 4 6 7 1 0 4 6 7 1 r r r r               解 对增广矩阵进行初等行变换化成行最简形

第四章线性方程组 11 -3 -1 3 3+3 2 5-4 3 1 1-3 01 3 7 1 2 4 4 01 2 4 5×(00 0 0 0 0 0 0 0 0 于是得到与原方程组同解的方程组 33 25* 5 4 3 x2 x3-尤4= 4

第四章 线性方程组 3 2 2 1 1 3 1 1 3 7 1 ~ 0 1 2 4 4 1 ( ) 0 0 0 0 0 4 r r r               1 2 3 3 5 1 0 2 4 4 3 7 1 ~ 0 1 2 4 4 0 0 0 0 0 r r            于是得到与原方程组同解的方程组 1 3 4 2 3 4 3 3 5 , 2 4 4 3 7 1 , 2 4 4 x x x x x x            

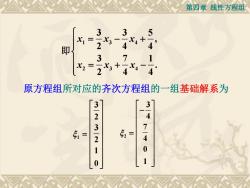
第四章线性方程组 3 3 5 即 2 4 3 X2= 53+ X4 原方程组所对应的齐次方程组的一组基础解系为 3 3 4 5= 3-2 7 52= 4 1 0 0 1

第四章 线性方程组 1 3 4 2 3 4 3 3 5 , 2 4 4 3 7 1 . 2 4 4 x x x x x x            即 原方程组所对应的齐次方程组的一组基础解系为 1 3 2 3 2 1 0         2 3 4 7 4 0 1        