《线性代数》课程教学课件（PPT讲稿，C）第三章 矩阵的运算 3-3 初等矩阵

第三章矩阵的运算 §3.3初等矩阵 初等矩阵的概念 二、初等矩阵的应用 三、小结思考题

第三章 矩阵的运算 三、小结 思考题 二、初等矩阵的应用 一、初等矩阵的概念 §3.3 初等矩阵

第三章矩阵的运算 一、初等矩阵的概念 定义1由单位矩阵E经过一次初等变换得到 的方阵称为初等矩阵。 三种初等变换对应着三种初等方阵 [1.对调两行或两列； 2.以数k≠0乘某行或某列； 3.以数k乘某行（列)加到另一行（列）上去

第三章 矩阵的运算 定义1 由单位矩阵 E 经过一次初等变换得到 的方阵称为初等矩阵. 三种初等变换对应着三种初等方阵.       以数 乘某行（列）加到另一行（列）上去． 以数 乘某行或某列； 对调两行或两列； k k 3. 2. 0 1.一、初等矩阵的概念

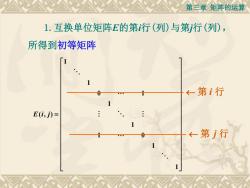
第三章矩阵的运算 1.互换单位矩阵E的第行（列）与第行（列）， 所得到初等矩阵 ←-第i行 E(i,j)= ←第j行

第三章 矩阵的运算 1 1 0 1 1 ( , ) 1 1 0 1 1 E i j                第 i 行  第 j 行 1.互换单位矩阵E的第i行(列)与第j行(列)， 所得到初等矩阵

第三章矩阵的运算 2.用非零常数乘单位矩阵E的第行（列）， 所得到初等矩阵 E(i(k= ←第i行

第三章 矩阵的运算 1 1 ( ( )) 1 1 E i k k           第 i 行 2.用非零常数k乘单位矩阵E的第i行(列), 所得到初等矩阵

第三章矩阵的运算 3.用常数乘单位矩阵E第行（第列）加到 第行（第列）上，所得到的初等矩阵 第行 E(jk),)= 第行

第三章 矩阵的运算 1 1 ( ( ) ) 1 1 k E j k i            ，  第i行  第j行 3.用常数k乘单位矩阵E第j行(第i列)加到 第i行(第j列)上,所得到的初等矩阵

第三章矩阵的运算 初等矩阵均可逆，其逆矩阵仍然是同类初等矩阵 E(i,j)=E(i,); E(k》'=E(》店 E(j(k),)=E((-k),). 对矩阵进行初等变换，可以用相应的初等矩阵 左乘或右乘矩阵来表示

第三章 矩阵的运算 1 1 1 ( , ) ( , ); 1 ( ( )) ( ( )); ( ( ), ) ( ( ), ) . E i j E i j E i k E i k E j k i E j k i        初等矩阵均可逆,其逆矩阵仍然是同类初等矩阵 对矩阵进行初等变换，可以用相应的初等矩阵 左乘或右乘矩阵来表示

第三章矩阵的运算 例 100 . n w 2 k0 0 21 22 . ka kan . kazn 00 1八41 2 431 as a12+ka32 (2) 21 A2 31y l32 b1b2b131 00 b13 b12 (3) b21 b22 b23 D22 b31 b32

第三章 矩阵的运算 11 12 21 22 31 32 1 0 (2) 0 1 0 0 0 1 k a a a a a a            11 31 12 32 21 22 31 32 a ka a ka a a a a          11 13 12 21 23 22 31 33 32 b b b b b b b b b        11 12 1 21 22 2 31 32 3 1 0 0 (1) 0 0 0 0 1 n n n a a a k a a a a a a               11 12 1 21 22 2 31 32 3 n n n a a a ka ka ka a a a           例 11 12 13 21 22 23 31 32 33 1 0 0 (3) 0 0 1 0 1 0 b b b b b b b b b           

第三章矩阵的运算 设 12 ●● an Ai2 Cin A= aj aj 00

第三章 矩阵的运算 11 12 1 1 2 1 2 1 2 n i i in j j jn m m mn a a a a a a A a a a a a a                        设

第三章矩阵的运算 对mXn矩阵A交换第行与第行 012 a12 aa ai2 an aj2 A= =E(i,j)A an 0j2 an ai2 ain am am2 。 0 0m2 就相当于以相应的阶初等矩阵E(i,)去左乘矩阵A:

第三章 矩阵的运算 对m×n矩阵A交换第i行与第j行 就相当于以相应的m阶初等矩阵E(i, j)去左乘矩阵A. ， E i j A a a a a a a a a a a a a a a a a a a a a a a a a A m m mn i i in j j jn n r r m m mn j j jn i i in n ~ ( , ) 1 2 1 2 1 2 11 12 1 1 2 1 2 1 2 11 12 1 1 2                                               

第三章矩阵的运算 对m×n矩阵A的第行乘以不为零的数k a11 d12 a A= aa ai2 kan kai2 ka in = E(i(kA am2 am am2 就相当于以相应的阶初等矩阵E(i()去左乘矩阵A

第三章 矩阵的运算 对m×n矩阵A的第i行乘以不为零的数k E i k A a a a ka ka ka a a a a a a a a a a a a A m m mn i i in n r k m m mn i i in n i~ ( ( )) 1 2 1 2 11 12 1 1 2 1 2 11 12 1                                      就相当于以相应的m阶初等矩阵E(i(k))去左乘矩阵A