《线性代数》课程教学课件（PPT讲稿，C）第一章 n阶行列式 1-2 行列式的性质

行列试 §1.2行列式的性质 行列式的性质 二、 应用举例 三、小结思考题

第一章 行列式 三、小结 思考题 二、应用举例 一、行列式的性质 §1.2 行列式的性质

第一章行列式 、 行列式的性质 利用行列式的定义计算行列式，特别是高阶 行列式，计算量相当大.为简化行列式的计算，下 面我们来讨论行列式的性质. 由行列式的定义式知，行列式可表示为第一行 的元素与其对应的代数余子式的乘积之和，即行列 式可按第一行的展开式，事实上，行列式可按任意 一行（列)展开. 有下面的重要定理

第一章 行列式 一 、行列式的性质 利用行列式的定义计算行列式，特别是高阶 行列式，计算量相当大.为简化行列式的计算，下 面我们来讨论行列式的性质. 由行列式的定义式知，行列式可表示为第一行 的元素与其对应的代数余子式的乘积之和，即行列 式可按第一行的展开式，事实上，行列式可按任意 一行（列）展开. 有下面的重要定理

第一章行列式 定理1.2.1n阶行列式等于它的任意一行（列）的元素 与其对应的代数余子式的乘积之和，即 D=41A+a2A2+.+0nAn(i=1,2,.,n） 或 D=1A+a2jA2j+.+0时A( j=1,2,.,n) 推论如果n阶行列式中的行所有元素除4：外都为 零，那么行列式就等于：与其对应的代数余子式 的乘积，即 D=anAj

第一章 行列式 定理1.2.1 n阶行列式等于它的任意一行(列)的元素 与其对应的代数余子式的乘积之和，即 1 1 2 2 . ( 1,2, , ) D i i i i in in  a A  a A   a A i   n 1 1 2 2 . ( 1, 2, , ) D j j j j nj nj  a A  a A   a A j   n 或 ij a ij 零，那么行列式就等于 a 推论 如果n阶行列式中的i行所有元素除 外都为 与其对应的代数余子式 的乘积，即 D ij ij  a A

第一章行列式 转置行列式： 1 12 设n阶行列式D= 21 L22 0n2 .ln 若把D中每一行元素换成同序数的列，得到 1 021 D'= 12 2 02 .: .lnn 行列式D'(或D')称为行列式D的转置行列式

第一章 行列式 设n阶行列式 nn a a a  22 11    n n a a a 2 12 1   1 2 21 n n a a a D     2 21 1 n n a a a   n n a a a 1 2 D 12   nn a a a  22 11 若把D中每一行元素换成同序数的列, 得到 ( ) . T 行列式D 或D 称为行列式D的转置行列式 转置行列式：

第一章行列式 性质1行列式与它的转置行列式相等. 例当=2时，11012 011421 结论成立 021022 012L22 说明 行列式中行与列具有同等的地位，因此行列 式的性质凡是对行成立的对列也同样成立

第一章 行列式 11 12 11 21 21 22 12 22 a a a a a a a a 例 当n=2时，  ,结论成立. 说明 行列式中行与列具有同等的地位,因此行列 式的性质凡是对行成立的对列也同样成立

第一章行列式 例如，上三角行列式 11 12 0 D= l22 Q2n 0 0 由定理1.2.1即得 1 0 0 D=D'= %12 l22 =411L22.0nm . Ain Qzn

第一章 行列式 例如，上三角行列式 11 12 1 22 2 . 0 . . . . . 0 0 . n n nn a a a a a D a  11 12 22 11 22 1 2 0 . 0 . 0 . . . . . . nn n n nn a a a D D a a a a a a     由定理1.2.1即得

第一章行列式 性质2互换行列式的两行（列，行列式变号。 证：用数学归纳法。 当m=2时，1412 结论成立 02122 11L2 假设对n-1阶行列式结论成立.对n阶行列式D

第一章 行列式 证： 用数学归纳法. 11 12 12 22 21 22 11 21 a a a a a a a a 当n=2时，   ，结论成立. 性质2 互换行列式的两行(列), 行列式变号. 假设对n-1阶行列式结论成立. 对n阶行列式D

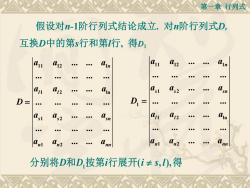
第一章行列式 假设对n-1阶行列式结论成立.对n阶行列式D, 互换D中的第s行和第行，得D1 11 12 n 1 012 n 12 01 as2 D= ●e。 D1= sn p Ain . @n2 ●● an 分别将D和D按第行展开(i≠S,),得

第一章 行列式 假设对n-1阶行列式结论成立. 对n阶行列式D, 11 12 1 1 2 ln 1 2 1 2 . . . . . . . . . . . . . . . . . . . . . . . n l l s s sn n n nn a a a a a a D a a a a a a  11 12 1 1 2 1 1 2 ln 1 2 . . . . . . . . . . . . . . . . . . . . . . . n s s sn l l n n nn a a a a a a D a a a a a a  互换D中的第s行和第l行, 得D1 1 分别将D和D 按第i行展开(i  s,l),得

第一章行列式 分别将D和D按第行展开(i≠S,),得 D-Ea(-1yMgD.-Ea(-1YN 其中M和N分别是D和D中元素a,的余子式，并且 N,是由M,互换两行得到的-1阶行列式，由归纳假 设M,=-N因此D=-D

第一章 行列式 1 分别将D和D 按第i行展开(i  s,l),得 1 1 1 ( 1) , ( 1) n n i j i j ij ij ij ij j j D a M D a N           1 1 -1 . ij ij ij ij ij ij ij M N D D a N M n M  N D  D 其中 和 分别是 和 中元素 的余子式，并且 是由 互换两行得到的 阶行列式，由归纳假 设 ，因此

第一章行列式 性质2互换行列式的两行（列），行列式变号。 通常以表示行列式的第行，以c表示行列式的第列， 交换，两行记作分r,而交换五两列记作C,分C 例如 1 7 5 175 17 5 71 5 6 6 2 =-3 5 8, 6 6 2 6 6 2 3 5 8 6 6 2 3 5 8 5 3 8

第一章 行列式 , . i i i j i j r i c i i j r  r i j c  c 通常以 表示行列式的第 行,以 表示行列式的第 列, 交换 ， 两行记作 而交换 ， 两列记作 例如 , 1 7 5 1 7 5 6 6 2   3 5 8 . 8 2 5 8 2 5   3 6 1 5 6 7 5 6 7 3 6 1 6 6 2 3 5 8 性质2 互换行列式的两行(列), 行列式变号