《高等数学》课程教学资源（PPT课件）第三章 微分中值定理与导数的应用_3-1 微分中值定理

第三章 微分中值定理 与导数的应用 罗尔中值定理 推厂 中值定理 拉格朗日中值定理 泰勒公式 柯西中值定理 (第三节) 研究函数性质及曲线性态 应用 利用导数解决实际问题

第三章 中值定理 应用 研究函数性质及曲线性态 利用导数解决实际问题 罗尔中值定理 拉格朗日中值定理 柯西中值定理 泰勒公式 (第三节) 推广 微分中值定理 与导数的应用

第一为 第三章 中值定理 罗尔(Role)定理 二、拉格朗日中值定理 三、柯西(Cauchy)中值定理 HIGH EDUCATION PRESS eOC①8 机动目录上页下页返回结束

一、罗尔( Rolle )定理 第一节 机动 目录 上页 下页 返回 结束 二、拉格朗日中值定理 三、柯西(Cauchy)中值定理 中值定理 第三章

一、 罗尔(Rolle)定理 费马(fermat)引理 y=f(x)在U(x)有定义， >f'(x)=0 且f(x)≤f(x),∫'(x)存在 证：设+△xUo.fo+Ax)3/0), (或2) 则f'()=1im(xo+△y-fx) △x→0 △x [f'(x)≥0(Ax→0) >f'(x0)=0 f(x)≤0（△x→0+） 证毕 HIGH EDUCATION PRESS 费马目录上页下页返回结束

费马(fermat)引理 一、罗尔( Rolle )定理 且 存在 (或) 证: 设 则  0  0 x y o 0 x 费马 目录 上页 下页 返回 结束 证毕

罗尔(Rolle)定理 =f(x) y=f(x)满足 (1)在区间[a,b]上连续 (2)在区间(a,b)内可导 bx (3)f(a)=f(b) >在(a,b)内至少存在一点5，使f'(5)=0. HIGH EDUCATION PRESS ◆0C08 机动目录上页下页返回结束

罗尔（ Rolle ）定理 满足: (1) 在区间 [a , b] 上连续 (2) 在区间 (a , b) 内可导 (3) f ( a ) = f ( b ) 使 f () = 0. x y o a b y = f (x)  在( a , b ) 内至少存在一点 机动 目录 上页 下页 返回 结束

注意： 1)定理条件条件不全具备，结论不一定成立.例如， x,0≤x<1 0,x=1 f(x)=x f(x)=x x∈[-1,1] x∈[0，] HIGH EDUCATION PRESS 机动目录上页下页返回结束

注意: 1) 定理条件条件不全具备, 结论不一定成立. 例如, 1 x y o 1 x y −1 o 1 x y o 机动 目录 上页 下页 返回 结束

例1.证明方程x-5x+1=0有且仅有一个小于1的 正实根 证：1)存在性 设f(x)=x5-5x+1,则f(x)在I0,1]连续，且 f(0)=1,f1)=-3.由介值定理知存在x∈(0,1)，使 f(x)=0,即方程有小于1的正根x 2)唯一性. 假设另有x1∈(0,1)，≠x,使f()=0,:f(x)在以 X0,为为端点的区间满足罗尔定理条件，在x0,x之间 至少存在一点5，使f'(5)=0. 但f'(x)=5(x4-1)<0,x∈(0,1)，矛盾，故假设不真！ HIGH EDUCATION PRESS 0eOC①8 机动目录上页下页返回结束

例1. 证明方程 ( ) 5 1, 5 f x = x − x + ( ) 0, f x0 = 有且仅有一个小于1 的 正实根 . 证: 1) 存在性 . 则 f (x) 在 [0 , 1 ] 连续 , 且 由介值定理知存在 (0,1), x0  使 即方程有小于 1 的正根 2) 唯一性 . 假设另有  f (x)在以 0 1 x , x 为端点的区间满足罗尔定理条件 , 在x0 , x1之间 至少存在一点 但 矛盾, 故假设不真! 设 机动 目录 上页 下页 返回 结束

二、拉格朗日中值定理 x) y=f(x)满足 (1)在区间[a,b]上连续 (2)在区间(a,b)内可导 少存在-点5e(a,b,使f5)=fb)-f@ 证：问题转化为证了)-b-@=0 b-a b-a 作辅助函数 P(x)=f(x)-M(b)-f(a)x b-a 显然，p(x)在[a,b]上连续，在(a,b)内可导，且 p(a)-b/a-a/b)=ob,由罗尔定理知至少存在一点 b-a 5E(a,b),使p'(5)=0,即定理结论成立 .证毕 号HIGH EDUCATION PRESS 拉氏目录上页下页返回结束

二、拉格朗日中值定理  ( )   (1) 在区间 [ a , b ] 上连续 满足: (2) 在区间 ( a , b ) 内可导 至少存在一点 使 . ( ) ( ) ( ) b a f b f a f − −   =  x y o a b y = f (x) 思路: 利用逆向思维找出一个满足罗尔定理条件的函数 作辅助函数 显然 , 在 [ a , b ] 上连续 , 在 ( a , b ) 内可导, 且 证: 问题转化为证 (x) = f (x) x b a f b f a − − − ( ) ( ) (a) 由罗尔定理知至少存在一点 即定理结论成立 . =(b), b a b f a a f b − − = ( ) ( ) 拉氏 目录 上页 下页 返回 结束 0 ( ) ( ) ( ) = − −  − b a f b f a f  证毕

拉格朗日中值定理的有限增量形式： 令a=x0,b=x0+△x,则 △y=f'(x+0△x)△x(0<0<1) 推论：若函数f(x)在区间1上满足f'(x)=0,则f(x) 在1上必为常数 证：在I上任取两点，x2(x1<x2),在[x1,x2]上用拉 日中值公式，得 f(x2)-f(x)=∫'(5)(x2-x)=0(<5<x2) .f(x2)=f(x) 由1，x2的任意性知，f(x)在1上为常数 等HIGH EDUCATION PRESS 机动目录上页下页返回结束

拉格朗日中值定理的有限增量形式: 推论: 若函数 在区间 I 上满足 则 在 I 上必为常数. 证: 在 I 上任取两点 日中值公式 , 得 = 0 由 的任意性知, 在 I 上为常数 . ( ) (0 1) y = f  x0 + x x   令 则  机动 目录 上页 下页 返回 结束

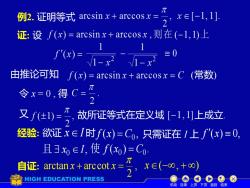
例2.证明等式arcsinx+arccosx= 2x∈-1，J 证：设f(x)=arcsinx+arccosx,则在(-l,l)上 f'(x)= ≡0 1-x2 v1-x 由推论可知f(x)=arcsinx+arccosx=C(常数) 令x=0,得C= 2 又fE1)=, 故所证等式在定义域[-1,1]上成立 经验：欲证x∈I时f(x)=Co,只需证在1上f'(x)≡0， 且3x0∈I,使f(o)=Co 自证：arctanx+arccotx= 、xe(-∞，+0 HIGH EDUCATION PRESS 动目录上页下页返回结束

例2. 证明等式 证: 设 由推论可知 (常数) 令 x = 0 , 得 又 故所证等式在定义域 上成立. 自证: , x(−, + ) 2 arctan arccot  x + x = 经验: 欲证 xI 时 ( ) , C0 f x = 只需证在 I 上 f (x)  0, , 0 且  x I ( ) . 0 C0 使 f x = 机动 目录 上页 下页 返回 结束

例3.证明不等式 ,x0) 1+x 证：设f(t)=lnl+t),则f(u)在[0，x]上满足拉格朗日 中值定理条件，因此应有 f(x)-(0)=f'(5)(x-0),00) 1+x HIGH EDUCATION PRESS e0C①8 机动目录上页下页返回结束

例3. 证明不等式 证: 设 f (t) = ln(1+t) , 中值定理条件, 即 因为 故 ln(1 ) ( 0). 1  +   + x x x x x 因此应有 机动 目录 上页 下页 返回 结束