《高等数学》课程教学资源（PPT课件）第三章 微分中值定理与导数的应用_3-3 泰勒公式

第三节 第三章 泰勒(Taylor)公式 理论分析 用多项式近似表示函数一应用 近似计算 一、泰勒公式的建立 二、几个初等函数的麦克劳林公式 三、泰勒公式的应用 HIGH EDUCATION PRESS 机动目录上页下页返回结束

二、几个初等函数的麦克劳林公式 第三节 一、泰勒公式的建立 机动 目录 上页 下页 返回 结束 三、泰勒公式的应用 用多项式近似表示函数 — 应用 理论分析 近似计算 泰勒 ( Taylor )公式 第三章

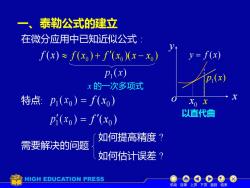
一、 泰勒公式的建立 在微分应用中已知近似公式 f(x)≈f(x)+f'(xx-x)） f(x Pi(x) x的一次多项式 特点p(xo)=f(xo) Xo x pi(x,)=f'(x)） 以直代曲 如何提高精度？ 需要解决的问题 如何估计误差？ HIGH EDUCATION PRESS 机动目录上页下页返回结束

特点: ( ) 0 = f x ( ) 0 = f  x 一、泰勒公式的建立 f (x) x y y = f (x) o ( ) ( )( ) 0 0 0  f x + f  x x − x 以直代曲 0 x ( ) 1 p x 在微分应用中已知近似公式 : 需要解决的问题 如何提高精度 ? 如何估计误差 ? x x 的一次多项式 机动 目录 上页 下页 返回 结束

1.求n次近似多项式pn(x),要求： Pn(x)=f(o)Pn(xo)=f'(x0)。,p(xo)=f(）》 这样的次多硕式存在6)+a2(x-xo)广+.+an(x-xo) 则 Ph(x)= a+2a2(x-x)+.+nan(x-x0)"-I ph(x)= 21a2+.+n(n-1)a,(x-x)"-2 。0·。·。0 p(x)= nlan ao Pn(xo)=f(xo), a ph(x0)=f"(xo), a2=P()=f"(o）.,an=aP%》(xo)=f(xo》 Pn(x)=f(o)+f(xo)(x-x0)+f"(xo)(x-x0)+ +af(xox-x0乃 在 HIGH EDUCATION PRESS 机动目录上页下页返回结束

这样的n 次多项式存在？ 1. 求 n 次近似多项式 要求: ( ) 2! 0 1 2 a p x n =  ( ), 0 = f  x  , ( ) 0 ( ) ! 1 a p x n n = n n ( ) 0 ( ) f x n = 故 pn (x) = ( ) 0 f x ( )( ) 0 0 + f  x x − x + 2 ! 1 ! 1 n n n f (x )(x x ) 0 0 ( ) + − ! 1 n 2 0 0 + f (x )(x − x ) 2! 1 机动 目录 上页 下页 返回 结束 令 pn (x) = 则 pn  (x) = pn (x) =  n p (n) (x) = n!a n ( ) 0 0 a p x = n ( ), 0 = f x ( ) 1 0 a p x n =  ( ), 0 = f  x a1 2 ( ) 2 0 + a x − x 1 0 ( ) − + + − n n  n a x x 2 2!a 2 0 ( 1) ( ) − + + − − n n  n n a x x a0 n n a (x x ) a (x x ) a (x x ) 0 2 + 1 − 0 + 2 − 0 ++ − 存在

泰勒中值定理： 若f(x)在包含xo的某开区间(a,b)内具有 直到n+1阶的导数，则当x∈(a,b)时，有 j)=f)+xX-)+(x-P+ 21 +((x-x,)”+R,) n! 其中R(x)= f(5 (x-x)”1(传在x与x之间② (n+1)川 公式①称为f(x)的n阶泰勒公式 公式②称为n阶泰勒公式的拉格朗日余项 HIGH EDUCATION PRESS 泰勒目录上页下页返回结束

公式 ① 称为 的 n 阶泰勒公式 . 公式 ② 称为n 阶泰勒公式的拉格朗日余项 . 泰勒中值定理 : 阶的导数 , 时, 有 ( ) 0 f x ( )( ) 0 0 + f  x x − x 2 0 0 ( ) 2! ( ) x x f x −  + + n n x x n f x ( ) ! ( ) 0 0 ( ) + − R (x) + n ① 其中 1 0 ( 1) ( ) ( 1)! ( ) ( ) + + − + = n n n x x n f R x  ② 则当 ) 0 ( 在 x 与x之间 泰勒 目录 上页 下页 返回 结束

注意到 Rn(x)=o[(x-xo)”] ③ 在不需要余项的精确表达式时，泰勒公式可写为 /)=f0)+f,Xx-)+wx-+ 21 +(x-xw+ox-x)门 n! 公式③称为n阶泰勒公式的佩亚诺Peano)余项 *可以证明 ∫(x)在点x,有直到n阶的导数 > ④式成立 HIGH EDUCATION PRESS 机动目录上页下页返回结束

公式 ③ 称为n 阶泰勒公式的佩亚诺(Peano) 余项 . 在不需要余项的精确表达式时 , 泰勒公式可写为 f (x0 ) + f (x0 )(x − x0 ) 0 ( 0 ) 2 + 2! ( ) x x f x −  + n n x x n f x ( ) ! ( ) 0 0 ( ) + − [( ) ] 0 n + o x − x ( ) [( ) ] 0 n n 注意到 R x = o x − x ③ ④ * 可以证明: ④ 式成立 机动 目录 上页 下页 返回 结束

f()=f(x)+(xox-x)+(-) 21 (( (n+1) 特例： (5在x与x之间) (1)当n=0时，泰勒公式给出拉格朗日中值定理 f(x)=f(xo)+f()(x-xo) (5在x0与x之间) (2)当n=1时，泰勒公式变为 /)=f)+x-x4x-月 可见f(x)≈f(xo)+f'(x,)x-xo) 2在与x之间 误差 -广5室0、 df HIGH EDUCATION PRESS 机动目录上页下页返回结束

特例: (1) 当 n = 0 时, 泰勒公式变为 f (x) = ( ) 0 f x ( )( ) 0 + f   x − x (2) 当 n = 1 时, 泰勒公式变为 给出拉格朗日中值定理 f (x) = ( ) 0 f x ( )( ) 0 0 + f  x x − x 2 0 ( ) 2! ( ) x x f −  +  可见 误差f (x) = ( ) 0 f x ( )( ) 0 0 + f  x x − x + 1 0 ( 1) ( ) ( 1)! ( ) + + − + + n n x x n f  2 0 0 ( ) 2! ( ) x x f x −  + n n x x n f x ( ) ! ( ) 0 0 ( ) + − d f ) 0 ( 在 x 与x之间) 0 ( 在 x 与x之间) 0 ( 在 x 与x之间 ) 0 ( 在 x 与x之间 机动 目录 上页 下页 返回 结束

在泰勒公式中若取x。=0,5=0x(0<0<1),则有 /)=0+f0x+0x4+/9O 21 n (n+1)！ 称为麦克劳林(Maclaurin)公式. 由此得近似公式 fx)s0)+0x+0x2++0x 21 n! 若在公式成立的区间上f+(x)≤M,则有误差估计式 M R,(x)≤ n+】 (n+D)1 HIGH EDUCATION PRESS 麦克劳林目录上页下页返回结束

称为麦克劳林（ Maclaurin ）公式 . 0 , (0 1) , x0 =  = x   则有 f (0)+ f (0)x 2 + 2! (0) x f  + n n x n f ! (0) ( ) + 在泰勒公式中若取 f (x) = ( ) 0 f x ( )( ) 0 0 + f  x x − x + 1 0 ( 1) ( ) ( 1)! ( ) + + − + + n n x x n f  2 0 0 ( ) 2! ( ) x x f x −  + n n x x n f x ( ) ! ( ) 0 0 ( ) + − ) 0 ( 在 x 与x之间 f (x)  f (0) + f (0)x + ( ) , ( 1) f x M n  + 则有误差估计式 1 ( 1)! ( ) + +  n n x n M R x 2 2! (0) x f  + n n x n f ! (0) ( ) + 若在公式成立的区间上 麦克劳林 目录 上页 下页 返回 结束 由此得近似公式

二、几个初等函数的麦克劳林公式 (1)f(x)=ex f()=e,f0(0)=1(k=1,2,） e"=1+x+* + n! 其中Rn(x)= (DI (0<θ<1) HIGH EDUCATION PRESS 机动目录上页下页返回结束

二、几个初等函数的麦克劳林公式 ( ) , (k ) x  f x = e (0) 1 ( 1,2, ) f (k ) = k =  x  e =1 + x 3! 3 x + + n ! x n + R (x) + n 2! 2 x + 其中 机动 目录 上页 下页 返回 结束

(2)f(x)=sinx 图例sinx :了)=m+k孕 k 2m (m=1,2,.) sinx =x- (2m-1）1 +R2m(x) 其中Rm(m)=（-Dcos(0 ）-x2m+1 (0<0<1) (2m+1)J HIGH EDUCATION PRESS O◆0C08 机动目录上页下页返回结束

( ) = sin(x + ) ( ) f x k   sin x = x 3! 3 x − 5! 5 x + (2 1)! 2 1 − + − m x m ( ) 2 R x + m 其中 R2m (x) = sin( ) 2 2 1   + + m x 2  k  2 (0) sin ( )  f k k =    = 0, k = 2m ( 1) , k = 2m −1 −1 − m (m =1,2, ) − 1 ( 1) − − m (0  1) 2m+1 x (2m +1)! ( 1) cos( x) m −  机动 目录 上页 下页 返回 结束 图例sin x

(3)f(x)=cosx 类似可得 cosx=1-2 ,+入+.+（刀交2の +R2m+l() (2m)I 其中 n4=-lco0:0<0< (2m+2)J HIGH EDUCATION PRESS 机动目录上页下页返回结束

(2 )! 2 m x m + 类似可得 cos x =1 2! 2 x − 4! 4 x + ( ) 2 1 R x + m+ 其中 R2m+1 (x) = (2m + 2)! ( 1) cos( ) 1 x m  + − (0  1) + m (−1) 2m+2 x 机动 目录 上页 下页 返回 结束