《高等数学》课程教学资源（PPT课件）第一章函数与极限_第五节极限运算法则

第五节极限运算法则 一、无穷小的运算法则 二、极限的四则运算法则 三、复合函数的极限运算法则 上顷下预返回城公式线与面数学家

第五节 极限运算法则 一、无穷小的运算法则 二、极限的四则运算法则 三、复合函数的极限运算法则

第五节极限运算法则 一、无穷小的运算法则 定理1有限个无穷小的和也是无穷小. 证明 定理2有界函数与无穷小的乘积是无穷小. 证明 推论1常数与无穷小的乘积是无穷小. 推论2有限个无穷小的乘积也是无穷小. 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 极限运算法则 一、无穷小的运算法则 定理1 有限个无穷小的和也是无穷小. 第五节 极限运算法则 证明 定理1 有限个无穷小的和也是无穷小. 考虑两个无穷的和. 设 0 , 0 , lim lim 0 0 = = → →   x x x x  > 0 . 0 lim 0 = →  x x 对于 , 2   1 > 0，当 0 0，当 0 0 , ( , ) 0  1 U x  是有界的，即  M > 0 使 | u |  M 对一切 成立. 0 lim 0 = →  x x  2 > 0， 当 | | . M    取  = min{ 1 , 2 }， 定理2 有界函数与无穷小的乘积是无穷小. 内 ( , ) 0  1 x U x   又设 则当 ( , ) 0  2 x U x   有 ( , ) x U x0    时，不等式 | u |  M 及 M  | | 同时成立. 推论1 常数与无穷小的乘积是无穷小. 推论2 有限个无穷小的乘积也是无穷小

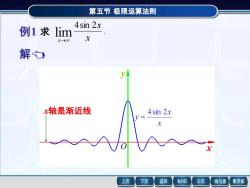
第五节极限运算法则 4sin 2x 例1求lim x→0 x 解 x轴是渐近线 4sin 2x 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 极限运算法则 例1 第五节 极限运算法则 解 例1 求 . 4sin 2 lim x x x→ , 1 (4sin 2 ) 4sin 2 x x x x  =  而 | 4sin 2x | 4 , 所以 4sin2x 是有界函数， 0 , 1 lim = x→ x  所以 x 1 是无穷小， 由定理2知， 当 x→ 时， x 4sin 2x 是无穷小. 0 . 4sin 2  lim = → x x x x x y 4sin 2 = x y x轴是渐近线 O 求 . 4sin 2 lim x x x→ x轴是渐近线 x x y 4sin 2 = x y O

第五节极限运算法则 二、极限的四则运算法则 定理3如果limf(x)=A,lmg(x)=B,那么 (1)lim[f(x)±g(x)】=limf(x)±limg(x)=A±B; (2)lim[f(x).g(x)]=lim f(x).lim g(x)=4.B; (3)若又有B≠0，则 lim f(x)lim f(x) A 8(x) lim g(x)B 证明(1①)证明(2)之 证明(3) 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 极限运算法则 二、极限的四则运算法则 定理3 如果 lim f (x) = A, lim g(x) = B , 那么 (1) lim[ f (x)  g(x)] = lim f (x)  lim g(x) = A B ; (2) lim[ f (x) g(x)] = lim f (x)lim g(x) = AB ; (3) 若又有 B  0，则 ( ) ( ) lim g x f x lim ( ) lim ( ) g x f x = . B A = 第五节 极限运算法则 证明 (1) 定理3 如果 lim f (x) = A , lim g(x) = B , 那么 (1) lim[ f (x)  g(x)] = lim f (x)  lim g(x) = A B ; 因为 lim f (x) = A , lim g(x) = B , 第四节 无穷小与无穷大 f x A x x x = → → ( ) lim ( ) 0 定理1(无穷小与函数极限的关系) ( ) , 0 lim ( ) 0 = + = → →   x x x f x A 第四节 f (x) = A+ , g(x) = B +  , ， 为无穷小， f (x)  g(x) = (A+)  (B + ) = (A B) + (  ) 第五节 极限运算法则 证明 (2) 因为 lim f (x) = A , lim g(x) = B , 第四节 无穷小与无穷大 f x A x x x = → → ( ) lim ( ) 0 定理1(无穷小与函数极限的关系) ( ) , 0 lim ( ) 0 = + = → →   x x x f x A 第四节 f (x) = A+ , g(x) = B +  , ， 为无穷小， f (x) g(x) = (A+)(B + ) = AB + (A + B + ) 定理3 如果 lim f (x) = A , lim g(x) = B , 那么 (2) lim[ f (x) g(x)] = lim f (x)lim g(x) = A B ; 第五节 极限运算法则 证明 (3) 定理3 如果 lim f (x) = A , lim g(x) = B , 那么 因为 lim f (x) = A , lim g(x) = B , 第四节 无穷小与无穷大 f x A x x x = → → ( ) lim ( ) 0 定理1(无穷小与函数极限的关系) ( ) , 0 lim ( ) 0 = + = → →   x x x f x A 第四节 f (x) = A+ , g(x) = B +  , ， 为无穷小， (3) 若又有 B  0，则 ( ) ( ) lim g x f x lim ( ) lim ( ) g x f x = . B A = 设 , ( ) ( ) B A g x f x  = − 则 B A B A − + + =    ( ) . ( ) 1    B A B B − + =

第五节极限运算法则 定理3中的(1)、(2)可推广到有限个函数的情形. 定理3有如下推论： 推论1如果imfw)存在，而c是常数，则 lim cf(c】=c limf (x). 推论2如果imfc)存在，而n是正整数，则 limlf (x)J=[limf (x)J. 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 极限运算法则 定理3中的(1)、(2) 可推广到有限个函数的情形. 定理3有如下推论： 推论1 如果 lim f (x) 存在，而 c 是常数，则 lim[cf (x)] = c limf (x) . 推论2 如果 lim f (x) 存在，而 n 是正整数，则 lim[f (x)]n = [limf (x)]n

第五节极限运算法则 关于数列也有类似的极限四则运算法则. 定理4设有数列{xn}和{yn}.如果 limx=4,limy=B, n->co n->00 那么 (1)lim(xn±yn)=A±B; n-o 2)lim(xn·yn)=A·B; (3)当yn≠0(n=1,2,)且B≠0时，lim 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 极限运算法则 关于数列也有类似的极限四则运算法则. 定理4 设有数列 { xn } 和 { yn } . 如果 x A， yn B， n n n = = → → lim lim 那么 (1) ( ) ; lim xn yn A B n  =  → (2) ( ) ; lim xn yn A B n  =  → (3) 当 yn  0 (n = 1, 2, .) 且 B  0 时， . lim B A y x n n n = →

第五节极限运算法则 定理5如果gpc)≥c),且limg()=a,lim)=b, 那么a≥b. 证明 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 极限运算法则 定理5 如果 (x)  (x)，且 lim(x)=a , lim(x)=b , 那么 a  b . 第五节 极限运算法则 证明 定理5 如果 (x)  (x)，且 lim(x)=a , lim(x)=b , 那么 a  b . 令 f (x) = (x) - (x)，则 f (x)  0 . 由定理3有 lim f (x) = lim[(x) – (x)] = lim(x) – lim(x) = a – b . 因为f (x)  0，极限的保号性 lim f (x)  0， 即 a – b  0，故 a  b . 证毕

第五节极限运算法则 例1求1im(2x-1) x- 解 x3-1 例2求limx2-5x+3 x→2 解 例1可以推广到有理函数（多项式），例2可以推广到 有理分式函数. 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 极限运算法则 例1 第五节 极限运算法则 解 例1 求 (2 1) . lim 1 − → x x (2 1) lim 1 − → x x 2 1 lim →1 lim →1 = − x x x 1 2lim 1 = − → x x = 21−1 =1. 求 (2 1) . lim 1 − → x x 例2 求 . 5 3 1 2 3 2 lim − + − → x x x x 第五节 极限运算法则 解 例2 求 . 5 3 1 2 3 2 lim − + − → x x x x 因为分母的极限不为零，故 5 3 1 2 3 2 lim − + − → x x x x ( 5 3) ( 1) 2 2 3 2 lim lim − + − = → → x x x x x 5 3 1 lim lim lim 2 2 2 3 2 − + − = → → → x x x x x x ( ) 5 2 3 ( ) 1 2 2 3 2 lim lim −  + − = → → x x x x 2 10 3 2 1 2 3 − + − = . 3 7 = − 例1可以推广到有理函数(多项式)，例2可以推广到 有理分式函数

第五节极限运算法则 设多项式 f(x)=ax”+ax"-+.+an, 则 limf(x)=aox+axo++a=f(xo) X→x0 设有理分式函数F(x)= P(x) 其中Px)、Q)都是 (x) 多项式，且2心)≠0，则 lim F(x)= P(xo .=F(Xo) X→Xg Q(x 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 极限运算法则 设多项式 ( ) , 1 0 1 n n n f x = a x + a x + + a −  则 ( ) ( ). 0 1 lim 0 0 1 0 0 f x a x a x a f x n n n x x = + + + = − →  设有理分式函数 , ( ) ( ) ( ) Q x P x F x = 其中 P(x)、Q(x) 都是 多项式，且 Q(x0 )  0，则 ( ). ( ) ( ) ( ) 0 0 0 lim 0 F x Q x P x F x x x = = →

第五节极限运算法则 x-3 例3求lim x3 x2-9 解己 2x-3 例4求1im )1 x2- 5x+4 解 2x3-3x 例5求limx-3x2+4x+1 解 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 极限运算法则 例3 求 . 9 3 2 3 lim − − → x x x 第五节 极限运算法则 解 例3 求 . 9 3 2 3 lim − − → x x x 因为分子分母的极限都为零，所以不能直接用 有理分式函数的极限运算公式. 因为 , ( 3)( 3) 3 9 3 2 − + − = − − x x x x x 而 x→3 时，x  3，即 x – 3  0，故上式中的致零因子 可以约去， 于是 9 3 2 3 lim − − → x x x ( 3)( 3) 3 lim 3 − + − = → x x x x 3 1 lim 3 + = x→ x . 6 1 = 致零因子 例4 求 . 5 4 2 3 2 1 lim − + − → x x x x 第五节 极限运算法则 解 因为分母的极限为零，所以不能直接用有理分 例4 求 . 5 4 2 3 2 1 lim − + − → x x x x 式函数的极限运算公式. 因为 2 3 5 4 2 1 lim − − + → x x x x 0 . 1 0 2 1 3 1 5 1 4 2 = − =  − −  + = 由无穷小与无穷大的关系，得 . 5 4 2 3 2 1 lim =  − + − → x x x x 例5 求 . 3 4 1 2 3 3 2 3 lim − + + − → x x x x x x 第五节 极限运算法则 解 例5 求 . 3 4 1 2 3 3 2 3 lim − + + − → x x x x x x 3 4 1 2 3 3 2 3 lim − + + − → x x x x x x 2 3 2 3 4 1 1 3 2 lim x x x x x − + + − = → = 2 . 分子分母除以 x 3