《高等数学》课程教学资源（PPT课件）第一章函数与极限_第二节数列的极限

第二节数列的极限 一、引例 二、数列极限的定义 三、收敛数列的性质 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 数列的极限 一、引例 二、数列极限的定义 三、收敛数列的性质

第二节数列的极限 一、引例 引例1割圆术求圆面积的近似值， 依次作圆内接正4×2"(n=0,1,2,.)边形，设A0表示 内接正方形面积，A表示内接正8 边形的面积，.，An表示内接正 4×2"边形的面积.这样就得到一 系列内接正多边形的面积： 正方形 A=2 A0,A1,.,An,· 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 数列的极限 一、引例 引例1 割圆术 求圆面积的近似值. 依次作圆内接正42 n (n = 0,1,2,.)边形, 设 A0 表示 内接正方形面积, A1 表示内接正8 边形的面积, . , 42 n 边形的面积. An 表示内接正 这样就得到一 系列内接正多边形的面积：

第二节数列的极限 A0,A1,.,An,., 它们构成一列有次序的数.当n越大，An越接近圆面 积的精确值，因此，当n趋于无穷大（记为n→o)时， Am就无限趋于圆面积的精确值. 我国古代数学家刘徽利用自己首创的割圆术，计算 到了内接正3072边形，得到了圆周率为3.14和3.1416 这两个近似值.在MathGS的工具箱中，算得的内接正 3072边形的面积约为3.1415895.因此刘徽首创的割圆 术在古代是一个伟大的发明. 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 数列的极限 它们构成一列有次序的数. 当 n 越大，An越接近圆面 积的精确值，因此，当 n 趋于无穷大(记为n→)时， An就无限趋于圆面积的精确值. 我国古代数学家刘徽利用自己首创的割圆术，计算 到了内接正3072边形，得到了圆周率为 3.14 和 3.1416 这两个近似值. 在MathGS的工具箱中，算得的内接正 3072边形的面积约为3.1415895. 因此刘徽首创的割圆 术在古代是一个伟大的发明

第二节数列的极限 在其他很多问题中也会碰到：对于得到的一列有次 序的数 X1,X2,·,Xn) 研究当→o时，这列数的变化趋势.于是就产生了数 列以及数列的极限 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 数列的极限 在其他很多问题中也会碰到： 对于得到的一列有次 序的数 研究当 n→ 时，这列数的变化趋势. 于是就产生了数 列以及数列的极限

第二节数列的极限 二、数列极限的定义 定义如果按照某一法则，对每个n∈N+,对应着 一个确定的实数xn,这些实数xn按照下标从小到大 排列得到的一个序列 X1X2,·,Xn, 就叫做数列，简记为数列{xn. 数列中的每一个数叫做数列的项，第项xn叫做数 列的一般项.例如， 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 数列的极限 二、数列极限的定义 定义 如果按照某一法则，对每个 n  N+ ，对应着 一个确定的实数 xn ，这些实数 xn 按照下标 n 从小到大 排列得到的一个序列 就叫做数列，简记为数列{ xn }. 数列中的每一个数叫做数列的项，第 n 项 xn 叫做数 列的一般项. 例如， x1 , x2 ,  , xn , 

第二节数列的极限 12 n 3 2 一般项 n n+1 Xn= n+1 2,4,.,2” 一般项xn=2”, 1 1 1 24 一般项 2 1,-1,.,(-1)1,. 一般项xn=(-1)+1, 1 n+(1,一般项 x,= n+(-1)r- 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 数列的极限 , , 1 , , 3 2 , 2 1   n + n 一般项 , +1 = n n xn 2 , 4 ,  , 2 ,  , n 一般项 2 , n n x = , , 2 1 , , 4 1 , 2 1  n  一般项 , 2 1 n n x = 1, 1, , ( 1) , , −  − n+1  一般项 ( 1) , +1 = − n n x , , ( 1) , , 2 1 2 , 1   n n n− + − 一般项 . ( 1) 1 n n x n n − + − =

第二节数列的极限 对于数列，我们要研究的问题是： 当→o时，数列{xn}是否能无限接近于某个确 定的常数？如果能，如何求这个常数？ 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 数列的极限 对于数列，我们要研究的问题是： 当 n→ 时，数列 { xn } 是否能无限接近于某个确 定的常数？ 如果能，如何求这个常数？

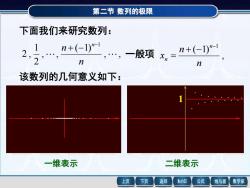
第二节数列的极限 下面我们来研究数列： 1 2 n+(-1)"-1 n+(-1)"- 2 n 一般项x,= n 该数列的几何意义如下： 一维表示 二维表示 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 数列的极限 下面我们来研究数列： , , ( 1) , , 2 1 2 , 1   n n n− + − 一般项 , ( 1) 1 n n x n n − + − = 该数列的几何意义如下： 一维表示 二维表示 1

第二节数列的极限 3.1 n+(-1)"- n+(-1)"-1 2 Xn n n 从几何上，我们发现，当n无限增大时，xm无限接 近常数1.那么，如何用数学语言来精确表示呢？ (1)xn与1的接近程度：用1xn-1|的大小来度量； (2)xm与1无限接近： |xm-1川无限小 |xm-1|<8,6是一个很小的正数，用来度量接近程度. (3)条件与结论：|xm-1|<e成立的条件是：n足 够大.例如 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 数列的极限  , ( 1) , , 2 1 2 , 1 n n n− + − , ( 1) 1 n n x n n − + − = 从几何上，我们发现，当 n 无限增大时，xn 无限接 近常数 1 . 那么，如何用数学语言来精确表示呢？ (1) xn 与 1 的接近程度: 用 | xn – 1 | 的大小来度量； (2) xn 与 1 无限接近: | xn – 1 | 无限小 | xn – 1 | < ， 是一个很小的正数，用来度量接近程度. (3) 条件与结论: | xn – 1 | <  成立的条件是：n 足 够大. 例如

第二节数列的极限 1 n+(-1)n-1 n+(-1)m- X= n n 当8=0.1时，因为 |x,-1= n+-l-110,即从第11项开始，后面所有的项都能满足 这一接近程度.又如，当e=0.001时，则n>1000. 可以证明：对任意给定的接近程度ε（不论它多么小）， 总可以找到这么一项，这项后面的所有项都能满足这 一接近程度. 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 数列的极限  , ( 1) , , 2 1 2 , 1 n n n− + − , ( 1) 1 n n x n n − + − = 当  = 0.1 时，因为 | −1| n x 1 ( 1) 1 − + − = − n n n 0.1. 1 =   = n 所以 n > 10, 即从第11项开始，后面所有的项都能满足 这一接近程度. 又如，当  = 0.001 时，则 n >1000 . 可以证明：对任意给定的接近程度 (不论它多么小), 总可以找到这么一项，这项后面的所有项都能满足这 一接近程度