《高等数学》课程教学资源（PPT课件）第二章导数与微分_第五节函数的微分

第五节函数的微分 一、微分的定义 二、微分的几何意义 三、微分的运算法则 四、微分在近似计算中的应用 上页 下页 返回 MathS 公式 线与面 数学家

第五节 函数的微分 一、微分的定义 二、微分的几何意义 三、微分的运算法则 四、微分在近似计算中的应用

第五节函数的微分 微分的定义 1.引例 一块正方形金属薄片受温度变化的影响，其边长由 变到xo+△x,问此薄片的面积改 Xo- Ax (Ax) x△x △x 变了多少？ 面积的改变量 A=x Xo △A=(x+△x)2-x号=2xA (△x)2 关于△x的线性函数 关于△x的高阶无穷小 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 函数的微分 一、微分的定义 0 x 0 x x x x x 0 2 (x) 2 0 A = x 1. 引例 一块正方形金属薄片受温度变化的影响，其边长由 x0 变到 x0 + x，问此薄片的面积改 变了多少？ 面积的改变量 A 2 0 2 0 = (x + x) − x 2 ( ) . 2 0 = x x + x 关于x的线性函数 关于x的高阶无穷小

第五节函数的微分 那么，对于任意函数y=f(),是否也有 Ay=f(x,+Ax)-f)=A△+o(△d 关于△x的线性函数 关于△x的高阶无穷小 本节将研究这一问题。 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 函数的微分 那么，对于任意函数 y = f (x)，是否也有 y ( ) ( ) 0 0 = f x + x − f x = Ax + o(x) . 关于x的线性函数 关于x的高阶无穷小 本节将研究这一问题

第五节函数的微分 2.定义 定义设函数y=fc)在某区间内有定义，x及o+△x 在这区间内，如果函数的增量△y=fK+△x)-fKo) 可表示为 △y=A△x+0(△x), 其中A是不依赖于△x的常数，那么称函数y=fx)在 点xo是可微的，而A△x叫做函数y=fc)在x处的微分 记作dy,即 dy=A△x. 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 函数的微分 2. 定义 定义 设函数y = f (x)在某区间内有定义, x0 及 x0+x 在这区间内，如果函数的增量 y = f (x0+x) – f (x0 ) 可表示为 y = A x + o(x)， 其中 A 是不依赖于 x 的常数，那么称函数 y = f (x) 在 点 x0 是可微的，而A x叫做函数y = f (x)在 x0 处的微分 记作 dy，即 dy = A x

第五节函数的微分 3.函数可微的充要条件 定理函数f)在点x处可微的充分必要条件是函 数fx)在点x处可导，并且dy=f'xo)△x. 证明之 因为dx=△x,所以dy=f'x)△x可写成 dy =f'(x)dx 由此可得 f'(x)= dv 导数也叫“微商” dx 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 函数的微分 3. 函数可微的充要条件 定理 函数 f (x) 在点 x0 处可微的充分必要条件是函 数 f (x) 在点 x0 处可导，并且 dy = f (x0 ) x . 第五节 函数的微分 证明 定理 函数 f (x) 在点 x0 处可微的充分必要条件是函 数 f (x) 在点 x0 处可导，并且 dy = f (x0 ) x . 必要性 设函数 y = f (x) 在 x0 处可微， 则有 y = Ax + o(x)， 两边除以 x 得 , ( ) x o x A x y   = +   于是 , ( ) lim 0 lim 0 A x o x A x y x x  =        = +    →  → 这说明函数 y = f (x) 在 x0 处可导，且 A = f (x0 ) . 因为 dx = x ，所以 dy = f (x) x 可写成 dy = f (x)dx ， 由此可得 . d d ( ) x y f  x = 导数也叫“微商

第五节函数的微分 例1求函数y=x2在x=1和x=3处的微分. 解 例2求函数y=Vx当x0=4,△x=0.03时的增量和 微分 解 在例2中，△y=0.007486,dy=0.0075,所以△y≈dy. 一般地，若y=f)在x处可微，且|△x|很小，则 △y=dy+o(dy)△y≈dy. 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 函数的微分 例1 求函数 y = x 2 在 x = 1 和 x = 3 处的微分. 第五节 函数的微分 解 例1 求函数 y = x 2 在 x = 1 和 x = 3 处的微分. 由微分的定义 dy = f (x0 )x 有 y f x d | x=1 = (1) = 2x , y f x d | x=3 = (3) = 6x . 例2 求函数 第五节 函数的微分 解 例2 求函数 y = x 当 x0 = 4 , x = 0.03 时的增量和 微分. 0 0 y = x + x − x = 4.03 − 4 = 2.007486 − 2 = 0.007486 , dy = f (x )x 0 x x =  2 0 1 4 0.03 = = 0.0075 . 在工具箱的函数求 值器中计算 y = x 当 x0 = 4 , x = 0.03 时的增量和 微分. 在例2中，y = 0.007486，dy = 0.0075，所以y  dy . 一般地，若 y = f (x) 在 x0 处可微，且 | x | 很小，则 y = dy + o(dy) y  dy

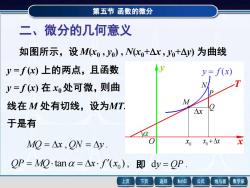
第五节函数的微分 二、微分的几何意义 如图所示，设Mx,yo),Nc+△x,Jyo+△y)为曲线 y=f()上的两点，且函数 y=f(x) y=fc)在x处可微，则曲 线在M处有切线，设为MT, △X 于是有 MQ=△x,QN=△y. ,+△ QP=MQ.tan=△x·f'(x),即dy=QP 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 函数的微分 二、微分的几何意义 如图所示，设 M(x0 , y0 ) , N(x0+x , y0+y) 为曲线 y = f (x) 上的两点，且函数 y = f (x) 在 x0 处可微，则曲 线在 M 处有切线，设为MT. 于是有 MQ = x , QN = y . tan ( ) , 0 QP = MQ  = x  f  x 即 dy = QP . M N Q P  0 x x + x 0 x x y T y = f (x) O

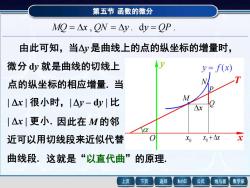
第五节函数的微分 MQ=△x,QN=△y.dy=QP. 由此可知，当△y是曲线上的点的纵坐标的增量时， 微分dy就是曲线的切线上 y=f(x) 点的纵坐标的相应增量。当 I△x|很小时，I△y-dy|比 M △X |△x|更小.因此在M的邻 近可以用切线段来近似代替 Xo +△x 曲线段.这就是“以直代曲”的原理. 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 函数的微分 MQ = x , QN = y . dy = QP . 由此可知，当y 是曲线上的点的纵坐标的增量时， 微分 dy 就是曲线的切线上 点的纵坐标的相应增量. 当 | x | 很小时，| y – dy | 比 | x | 更小. 因此在 M 的邻 近可以用切线段来近似代替 曲线段. 这就是“以直代曲”的原理. M N Q P  0 x x + x 0 x x y T y = f (x) O

第五节函数的微分 三、微分的运算法则 1.基本初等函数的微分公式 导数公式 微分公式 (x“)'=4x4- d(x“)=uxdr (sin x)'=cosx d(sin x)=cos xdx (cosx)'=-sin x d(cosx)=-sin xdx (tanx)'=sec2x d(tan x)=sec2 xdx (cotx)'=-csc2x d(cot x)=-csc2 xdx 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 函数的微分 三、微分的运算法则 1. 基本初等函数的微分公式 导 数 公 式 微 分 公 式 x x 2 (tan ) = sec (sin x) = cos x (cos x) = −sin x 1 ( ) −  =   x  x x x 2 (cot ) = −csc d(tan x) sec xdx 2 = d(sin x) = cos xdx d(cos x) = −sin xdx d(x ) x dx −1 =    d(cot x) csc xdx 2 = −

第五节函数的微分 导数公式 微分公式 (secx)'=secx.tan x d(secx)'=secx.tan xdx (cscx)'=-csCx·cotx d(cscx)=-cscx.cot xdx (a)'=aha(a>0,a≠1) d(a)=a*In adx(a>0,a≠1) (e*)'=e* d(e*)=e*dx og。y=la>0.a≠)d0og。=ldr(a>0,a≠ xIn a xIn a 血xy=1 d(nx)=Idx 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 函数的微分 导 数 公 式 微 分 公 式 (a ) = a ln a (a  0,a 1) x x x x (e ) = e ( 0, 1) ln 1 (log ) = a  a  x a x a x x 1 (ln ) = (csc x) = −csc x cot x d(a ) = a ln adx (a  0,a 1) x x x x x d(e ) = e d d ( 0, 1) ln 1 d(log ) = x a  a  x a x a x x x d 1 d(ln ) = d(csc x) = −csc x cot xdx (sec x) = sec x tan x d(sec x) = sec x tan xdx