《高等数学》课程教学资源（PPT课件）第一章函数与极限_第九节连续函数的运算与初等函数的连续性

第九节连续函数的运算与初等函数的连续性 一、连续函数的四则运算 二、反函数与复合函数的连续性 三、初等函数的连续性 上页 下页 返回 MathGS 公式 线与面 数学家

第九节 连续函数的运算与初等函数的连续性 一、连续函数的四则运算 二、反函数与复合函数的连续性 三、初等函数的连续性

第九节连续函数的运算与初等函数的连续性 一、连续函数的四则运算 定理1在某点连续的有限个函数经有限次和、差、 积、商（分母不为0）运算，结果仍是一个在该点连续的 函数. (利用极限的四则运算法则证明) 例如，Sinx,c0Sx都在(-oo,+oo)连续， sin x cOSx tanx= -cotx= 在其定义域内连续。 cos x sin x 上页 下页 返回 MathGS 公式 线与面 数学家

第九节 连续函数的运算与初等函数的连续性 一、连续函数的四则运算 在其定义域内连续. 定理1 在某点连续的有限个函数经有限次和 、差 、 ( 利用极限的四则运算法则证明) 积 、商(分母不为 0) 运算, 结果仍是一个在该点连续的 例如, 都在(- , + ) 连续， 函数

第九节连续函数的运算与初等函数的连续性 二、反函数与复合函数的连续性 1.反函数的连续性 定理2如果函数y=f(x)在区间I上单调增加（或单 调减少)且连续，那么它的反函数x=f)也在对应的 区间I,={y|y=fc),x∈Lx}上单调增加（或单调减少） 且连续。 证明略。 上页 下页 返回 MathGS 公式 线与面 数学家

第九节 连续函数的运算与初等函数的连续性 二、反函数与复合函数的连续性 定理2 如果函数 y = f (x) 在区间 Ix 上单调增加(或单 调减少)且连续，那么它的反函数 x = f -1 (y) 也在对应的 区间 Iy = { y | y = f (x) , x  Ix } 上单调增加(或单调减少) 且连续. 证明略. 1. 反函数的连续性

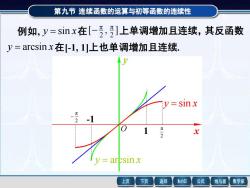
第九节连续函数的运算与初等函数的连续性 例如，y=sinx在[-乃，]上单调增加且连续，其反函数 y=arcsinx.在[-l,1]上也单调增加且连续， sinx π 上页 下页 返回 MathGS 公式 线与面 数学家

第九节 连续函数的运算与初等函数的连续性 例如, y = sin x 在 上单调增加且连续，其反函数 y = arcsin x 在[-1, 1]上也单调增加且连续. y = sin x y = arcsin x -1 1 2 π − 2 π x y O

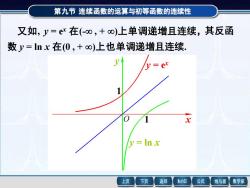
第九节连续函数的运算与初等函数的连续性 又如，y=ex在(-o,+o∞)上单调递增且连续，其反函 数y=lnx在(0，+o)上也单调递增且连续， er y=Inx 上页 下页 返回 MathGS 公式 线与面 数学家

第九节 连续函数的运算与初等函数的连续性 y = ex 在(- , + )上单调递增且连续， 数 y = ln x 在(0 , + )上也单调递增且连续. 又如, 其反函 y = ex y = ln x x y 1 1 O

第九节连续函数的运算与初等函数的连续性 2.复合函数的连续性 定理3设函数y=fg(x由函数u=g心)与函数 y=f(回复合而成，U(xo)cDg·若limg(x)=,而 函数y=f()在u=uo连续，则 lim f[g()]=lim f(u)=f(uo), x->X0 u-→l0 或 limf[g(x】=f[limg(x] 证明略。 上页 下页 返回 MathGS 公式 线与面 数学家

第九节 连续函数的运算与初等函数的连续性 2. 复合函数的连续性 定理3 设函数 y = f [g(x)] 由函数 u = g(x) 与函数 y = f (u) 复合而成， ( ) . 0 Df g U x    若 ( ) , lim 0 0 g x u x x = → 而 函数 y = f (u) 在 u = u0 连续， 则 [ ( )] ( ) ( ) , lim lim 0 0 0 f g x f u f u x x u u = = → → 或 [ ( )] [ ( )]. lim lim 0 0 f g x f g x x→x x→x = 证明略

第九节连续函数的运算与初等函数的连续性 定理4设函数y=fg心】由函数u=gx)与函数 y=f)复合而成，U(x)cDg·若函数u=g)在x= x连续，且gc0)=,而函数y=f)在u=连续， 则复合函数y=fg心】在x=连续， 证明略。 上页 下页 返回 MathGS 公式 线与面 数学家

第九节 连续函数的运算与初等函数的连续性 定理4 设函数 y = f [g(x)] 由函数 u = g(x) 与函数 y = f (u) 复合而成， ( ) . 0 Df g U x    若函数 u = g(x) 在 x = x0 连续，且 g(x0 ) = u0 ，而函数 y = f (u) 在 u = u0 连续, 则复合函数 y = f [g(x)] 在 x = x0 连续. 证明略

第九节连续函数的运算与初等函数的连续性 例如，y=sin二 是由连续函数链 X y=Sinu,u∈(-o,+oo) x∈R* 复合而成，因此y=sin在x∈R*上连续 上页 下页 返回 MathGS 公式 线与面 数学家

第九节 连续函数的运算与初等函数的连续性 例如, 是由连续函数链 * xR 因此 在 * 复合而成 , xR 上连续

第九节连续函数的运算与初等函数的连续性 三、初等函数的连续性 基本初等函数在定义域内连续 连续函数经四则运算仍连续 连续函数的复合函数连续 一切初等函数在定义区间内连续. 上页 下页 返回 MathGS 公式 线与面 数学家

第九节 连续函数的运算与初等函数的连续性 基本初等函数在定义域内连续 连续函数经四则运算仍连续 连续函数的复合函数连续 三、初等函数的连续性 一切初等函数在定义区间内连续

第九节连续函数的运算与初等函数的连续性 1+x2-1 例1求lim x→0 解 例2求lim log(1+x) 解 上页 下页 返回 MathS 公式 线与面 数学家

第九节 连续函数的运算与初等函数的连续性 例1 求 第九节 连续函数的运算与初等函数的连续性 解 例1 求 . 1 1 2 0 lim x x x + − → x x x 1 1 2 0 lim + − → ( )( ) ( 1 1) 1 1 1 1 2 2 2 0 lim + + + − + + = → x x x x x 1 1 2 0 lim + + = → x x x 2 0 = = 0 . . 1 1 2 0 lim x x x + − → 例2 求 第九节 连续函数的运算与初等函数的连续性 解 例2 求 . log (1 ) lim 0 x x a x + → x x a x log (1 ) lim 0 + → x a x x 1 0 log (1 ) = lim + → log e = a . ln 1 a = . log (1 ) lim 0 x x a x + →