《高等数学》课程教学资源（PPT课件）第二章导数与微分_第一节导数概念

第一节导数的概念 一、引例 二、导数的定义 三、导数的几何意义 四、可导与连续的关系 上页 下页 返回 MathGS 公式 线与面 数学家

第一节 导数的概念 一、引例 二、导数的定义 三、导数的几何意义 四、可导与连续的关系

第一节导数的概念 一、引例 引例1直线运动的速度 对于匀速直线运动有 经过的路程 平均速度= 所花的时间 其特点是：任一时刻的瞬时速度都相等，且等于任一时 间间隔上的平均速度， 上述公式也可用来求变速直线运动在某一时间间隔上 的平均速度. 上页 下页 返回 MathGS 公式 线与面 数学家

第一节 导数的概念 一、引例 引例1直线运动的速度 对于匀速直线运动有 平均速度 = 经过的路程 所花的时间 其特点是：任一时刻的瞬时速度都相等，且等于任一时 上述公式也可用来求变速直线运动在某一时间间隔上 的平均速度. 间间隔上的平均速度

第一节导数的概念 我们知道，自由落体运动的位置函数为5=28， 其中g为重力加速度， 自由落体运动是变速运动，随着时 的增加，物体落下的速度会越来越快， 对于该运动，利用前面的公式，容易 求出它在任意时间间隔上的平均速度 Bai&a国 时间间隔 1,2 [3,4 [5,6 [6,81 平均速度 1.5 3.5 5.5 14 那么变速直线运动的瞬时速度如何求呢？ 上页 下页 返回 MathGS 公式 线与面 数学家

第一节 导数的概念 我们知道，自由落体运动的位置函数为 , 2 1 2 s = gt 其中 g 为重力加速度. 自由落体运动是变速运动，随着时 的增加，物体落下的速度会越来越快. 对于该运动，利用前面的公式，容易 求出它在任意时间间隔上的平均速度. 时间间隔 平均速度 [1 , 2] [3 , 4] [5 , 6] 1.5 3.5 5.5 [6 , 8] 14 那么变速直线运动的瞬时速度如何求呢？

第一节导数的概念 设一动点作变速直线运动，其位置函数为s=s), 现在来求它在时刻t的瞬时速度， 为此，在6处取一时间间隔△，于是终止时刻为 t=to+△t. △t=t-t to 则动点在时间间隔△上的平均速度为 s(t)-s(to) t-to 由此可得瞬时速度为 v=lim s(t)-s(to) t→t0 t-to 上页 下页 返回 MathGS 公式 线与面 数学家

第一节 导数的概念 设一动点作变速直线运动，其位置函数为 s = s(t)， 现在来求它在时刻 t0 的瞬时速度. 为此，在 t0 处取一时间间隔 t，于是终止时刻为 t0 t t t = t – t0 则动点在时间间隔 t 上的平均速度为 . ( ) ( ) 0 0 t t s t s t v − − = 由此可得瞬时速度为 . ( ) ( ) 0 0 lim 0 t t s t s t v t t − − = → t = t0 + t

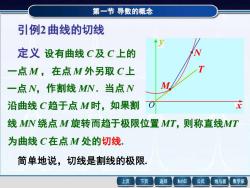
第一节导数的概念 引例2曲线的切线 定义设有曲线C及C上的 一点M,在点M外另取C上 一点N,作割线MN.当点N M 沿曲线C趋于点M时，如果割 线MN绕点M旋转而趋于极限位置MT,则称直线MT 为曲线C在点M处的切线 简单地说，切线是割线的极限 上页 下页 返回 MathGS 公式 线与面 数学家

第一节 导数的概念 引例2曲线的切线 定义 设有曲线 C 及 C 上的 一点 M ，在点 M 外另取 C 上 一点 N，作割线 MN . 当点 N 沿曲线 C 趋于点 M 时，如果割 线 MN 绕点 M 旋转而趋于极限位置 MT，则称直线MT 为曲线 C 在点 M 处的切线. 简单地说，切线是割线的极限. M N T x y O

第一节导数的概念 线的动画演示 a 上页 下页 返回 MathS 公式 线与面 数学家

第一节 导数的概念 切线的动画演示

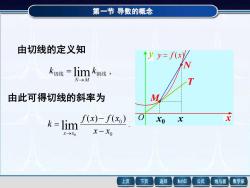
第一节导数的概念 由切线的定义知 ↑yy=fx/ k切线=limk线， N-M 由此可得切线的斜率为 M klim f(x)-f(xo) O Xo x→x0 x-Xo 上页 下页 返回 MathGS 公式 线与面 数学家

第一节 导数的概念 由切线的定义知 , k 切线 limk 割线 N→M = . ( ) ( ) 0 0 lim 0 x x f x f x k x x − − = → 由此可得切线的斜率为 M N T x0 x y = f (x) x y O

第一节导数的概念 引例1中的瞬时速度为 v=lim s(t)-s(to) 1->to t-to 引例2中切线的斜率为k=lim f(x)-f(xo) X→x0 x-xo 尽管在这两个引例中，所求量的具体意义不同，但最 终所求量的计算公式相同.因此需要对这种运算进行研 究，于是就产生了导数 上页 下页 返回 MathGS 公式 线与面 数学家

第一节 导数的概念 引例1中的瞬时速度为 . ( ) ( ) 0 0 lim 0 t t s t s t v t t − − = → . ( ) ( ) 0 0 lim 0 x x f x f x k x x − − = → 引例2中切线的斜率为 尽管在这两个引例中，所求量的具体意义不同，但最 终所求量的计算公式相同. 因此需要对这种运算进行研 究，于是就产生了导数

第一节导数的概念 二、导数的定义 1.函数在一点处的导数与导函数 定义设函数y=f:)在点x的某个邻域内有定义， 当自变量x在x0处取得增量△x(点xo+△x仍在该邻 域内)时，相应的函数取得增量△y=fx,+△)-f) 如果极限1m岩存在，则称函数y=f田在点处可 导，并称这个极限为函数y=)在点x处的导数， 记为f'c),即 上页 下页 返回 MathGS 公式 线与面 数学家

第一节 导数的概念 二、导数的定义 1. 函数在一点处的导数与导函数 定义 设函数 y = f (x) 在点 x0 的某个邻域内有定义, 当自变量 x 在 x0 处取得增量x (点 x0 + x 仍在该邻 域内) 时，相应的函数取得增量 y = f (x0 + x) – f (x), 如果极限 x y x    → lim 0 存在，则称函数 y = f (x) 在点 x0 处可 导，并称这个极限为函数 y = f (x) 在点 x0 处的导数， 记为 f (x0 )，即

第一节导数的概念 f(xo)=lim f(x+△x)-f(xo) △x-→0 △x 也可记作 y儿 dy 或 df(x) x=xo dx x=Xo 定义公式的等价形式 f()=lim f(x+△x)-f(x) Ar->0 △x f(x)-f(xo) f(xo)=lim f(xo+h)-f(xo)f(xo)=lim h→0 h →x0 x-Xo 上页 下页 返回 MathGS 公式 线与面 数学家

第一节 导数的概念 , ( ) ( ) ( ) 0 0 0 0 0 lim lim x f x x f x x y f x x x  +  − =    =  →  → 也可记作 0 0 d d | , x x x x x y y = =  或 . d d ( ) 0 x x x f x = 定义公式的等价形式 x f x x f x f x x  +  −  =  → ( ) ( ) ( ) 0 0 0 0 limh f x h f x f x h ( ) ( ) ( ) 0 0 0 0 lim + −  = → 0 0 0 ( ) ( ) ( ) lim 0 x x f x f x f x x x − −  = →