《高等数学》课程教学资源（PPT课件）第三章微分中值定理与导数的应用_第四节函数的单调性与曲线的凹凸性

第四节函数的单调性与曲线的凹凸性 一、函数单调性的判定法 二、曲线的凹凸性与拐点 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 函数的单调性与曲线的凹凸性 一、函数单调性的判定法 二、曲线的凹凸性与拐点

第四节函数的单调性与曲线的凹凸性 、 函数单调性的判定法 1.函数单调性的定义 单调增x1fc2) 直接用定义来判别函数的单调性就是要比较当x<x2 时fc)与fx2)的大小.这在本章之前有时是很困难的， 但现在有了微分中值定理，这种做法就变得容易了， 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 函数的单调性与曲线的凹凸性 1. 函数单调性的定义 一、函数单调性的判定法 单调性 单调增 x1 f (x2 ) 直接用定义来判别函数的单调性就是要比较当x1< x2 时 f (x1 ) 与 f (x2 ) 的大小. 这在本章之前有时是很困难的, 但现在有了微分中值定理，这种做法就变得容易了

第四节函数的单调性与曲线的凹凸性 因为由微分中值定理，有 fx2)-f(x)=f'(月x2-x1). 因此比较f(x)与fx2)的大小（即判别函数fx)的单调 性)即变成判别一阶导数f'x)的符号 下面从图形上来验证这个结论.设 f(x)=xsin x, 则 f(x)=sin x+xcosx. 在一个坐标系中同时绘制fx)与f'x)的图形如下， 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 函数的单调性与曲线的凹凸性 因为由微分中值定理，有 f (x2 ) – f (x1 ) = f ()(x2 – x1 ). 因此比较 f (x1 ) 与 f (x2 ) 的大小(即判别函数 f (x) 的单调 性) 即变成判别一阶导数 f (x) 的符号. 下面从图形上来验证这个结论. 设 f (x) = xsin x , 则 f (x) = sin x + x cos x . 在一个坐标系中同时绘制 f (x) 与 f (x) 的图形如下

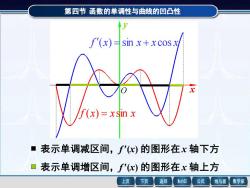
第四节函数的单调性与曲线的凹凸性 f(x)=sin x+xcosx (x)=xsinx ■ 表示单调减区间，f'x)的图形在x轴下方 表示单调增区间，f'x)的图形在x轴上方 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 函数的单调性与曲线的凹凸性 表示单调减区间，f (x) 的图形在 x 轴下方 表示单调增区间，f (x) 的图形在 x 轴上方 f (x) = xsin x f (x) = sin x + x cos x x y O

第四节函数的单调性与曲线的凹凸性 2.函数单调性的判定法 定理1设函数y=fx)在[a,b]上连续，在(a,b) 内可导 (1)如果在(a,b)内f')>0,那么函数y=fx)在 [a,b1上单调增加； (2)如果在(a,b)内f'x)<0,那么函数y=fx)在 [a,上单调减少. 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 函数的单调性与曲线的凹凸性 2. 函数单调性的判定法 定理1 设函数 y = f (x) 在 [a , b] 上连续，在 (a , b) 内可导. (1) 如果在 (a , b) 内 f (x) > 0，那么函数y = f (x) 在 [a , b] 上单调增加； (2) 如果在 (a , b) 内 f (x) < 0，那么函数 y = f (x) 在 [a , b] 上单调减少

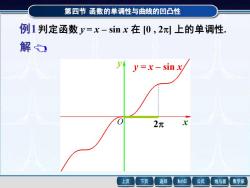
第四节函数的单调性与曲线的凹凸性 例1判定函数y=x-sinx在0,2π上的单调性. 解 y=x-sin x 2π 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 第四节 函数的单调性与曲线的凹凸性 函数的单调性与曲线的凹凸性 解 例1 判定函数 y = x – sin x 在 [0 , 2] 上的单调性. 因为在 (0 , 2) 内 y = 1 – cos x > 0 , 所以函数 y = x – sin x 在 [0 , 2] 上的单调增加. 事实上该函数在整个 定义域 (- , + ) 上都是 单调增加的. 2 y = x – sin x x y O 例1 判定函数 y = x – sin x 在 [0 , 2] 上的单调性. 2 y = x – sin x x y O

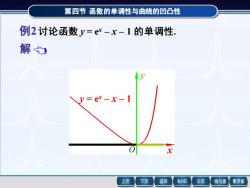
第四节函数的单调性与曲线的凹凸性 例2讨论函数y=ex-x-1的单调性. 解 、y=er-x-1 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 第四节 函数的单调性与曲线的凹凸性 函数的单调性与曲线的凹凸性 解 例2 讨论函数 y = ex – x – 1 的单调性. 函数的定义域为 (- , + ) . y = ex – 1 , 当 x 0 时，y > 0，所以函数 y = ex – x – 1 在 [0 , + ) 上单调增加. y = ex – x – 1 x y O 例2 讨论函数 y = ex – x – 1 的单调性. y = ex – x – 1 x y O

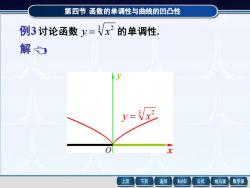
第四节函数的单调性与曲线的凹凸性 例3讨论函数y=Vx2的单调性. 解 y=Vx 上页 下页 返回 MathS 公式 线与面 数学家

第四节 第四节 函数的单调性与曲线的凹凸性 函数的单调性与曲线的凹凸性 解 函数的定义域为 (- , + ) . 当 x 0 时，y > 0，所以函数 在 [0 , + ) 上单调增加. 例3 讨论函数 3 2 y = x 的单调性. , 3 2 3 x y  = 当 x = 0 时，y 不存在. 3 2 y = x x y O 例3 讨论函数 3 2 y = x 的单调性. 3 2 y = x x y O

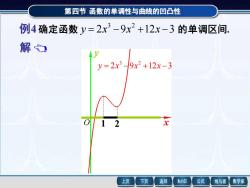
第四节函数的单调性与曲线的凹凸性 例4确定函数y=2x3-9x2+12x-3的单调区间. 解 y=2x39x2+12x-3 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 第四节 函数的单调性与曲线的凹凸性 函数的单调性与曲线的凹凸性 解 函数的定义域为 (- , + ) . 6 18 12 6( 1)( 2) , 2 y  = x − x + = x − x − 例4 确定函数 2 9 12 3 3 2 y = x − x + x − 的单调区间. 解得驻点为 x1 = 1 , x2 = 2 . y y (-, 1) 1 (1, 2) 2 (2, +) + 0 – 0 + 2 1 单调增区间：(-, 1)  (2, +)； 单调减区间：(1, 2) . 2 9 12 3 3 2 y = x − x + x − x y O 1 2 例4 确定函数 2 9 12 3 3 2 y = x − x + x − 的单调区间. 2 9 12 3 3 2 y = x − x + x − x y O 1 2

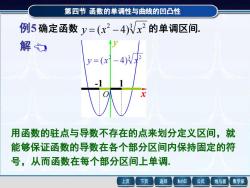
第四节函数的单调性与曲线的凹凸性 例5确定函数y=(x2-4)/x2的单调区间. 解 y=(x 4)N -1 用函数的驻点与导数不存在的点来划分定义区间，就 能够保证函数的导数在各个部分区间内保持固定的符 号，从而函数在每个部分区间上单调. 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 第四节 函数的单调性与曲线的凹凸性 函数的单调性与曲线的凹凸性 解 函数的定义域为 (- , + ) . , 3 8( 1) 3 2 x x y −  = 驻点为 x1 = -1 , x2 = 1 . y y (-, -1) -1 (-1, 0) 0 (0, 1) – 0 + 不 – -3 0 单调增区间：[-1, 0][1, +)；单调减区间： 例5 确定函数 2 3 2 y = (x − 4) x 的单调区间. 当 x = 0 时，y不存在， 1 (1, +) 0 + -3 (-, -1][0, 1]. 2 3 2 y = (x − 4) x -1 1 x y O 例5 确定函数 2 3 2 y = (x − 4) x 的单调区间. 用函数的驻点与导数不存在的点来划分定义区间，就 能够保证函数的导数在各个部分区间内保持固定的符 号，从而函数在每个部分区间上单调. 2 3 2 y = (x − 4) x -1 1 x y O