《高等数学》课程教学资源（PPT课件）第五章定积分_第三节定积分的换元法和分部积分法

第三节定积分的换元法和分部积分法 一、定积分的换元法 二、定积分的分部积分法 上页下页 返回Math6公式 线与面数学家

第三节 定积分的换元法和分部积分法 一、定积分的换元法 二、定积分的分部积分法

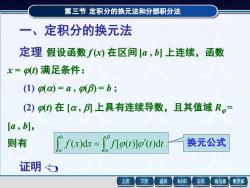
第三节定积分的换元法和分部积分法 一、定积分的换元法 定理假设函数fw)在区间[a,)上连续，函数 x=p)满足条件： (1)p(叫=a,(=b； 2)p)在[a,上具有连续导数，且其值域R。= [a,b], 则有 f(x)x=(dr 换元公式 证明 上页 下页 返回 MathGS 公式 线与面 数学家

第三节 定积分的换元法和分部积分法 一、定积分的换元法 定理 假设函数 f (x) 在区间 [a , b] 上连续，函数 x = (t) 满足条件： (1) () = a , () = b ; (2) (t) 在 [ , ] 上具有连续导数，且其值域 R = [a , b]， 则有 ( )d [ ( )] ( )d .   =    f x x f  t  t t b a 换元公式 第三节 定积分的换元法和分部积分法 证明 (1) () = a , () = b ; (2) (t) 在 [ , ] 上具有连续导数，且其值域 R = [a , b]， 假设 F(x) 是 f (x) 的一个原函数，则 f (x)dx F(b) F(a). b a = −  另一方面，记 (t) = F[(t)]，则 Φ(t) = f [(t)](t) , 于是 [( )] ( )d ( ) ()    f t  t t = Φ −Φ = F[()]− F[()] = F(b) − F(a) ( )d .  = b a f x x 证毕

第三节定积分的换元法和分部积分法 几点说明： (1)用x=p()换元时，积分限也要换成新变量的积 分限（换元必换限）； (2)求出f[p'的一个原函数后，不需代回 原来的变量，直接计算(-()即可. 3)换元公式相当于不定积分的第二换元积分法，反 过来用换元公式即为凑微分法，用凑微分法能直接算出 原函数时，可以不换元 上页 下页 返回 MathGS 公式 线与面 数学家

第三节 定积分的换元法和分部积分法 几点说明： (1) 用 x = (t) 换元时，积分限也要换成新变量的积 分限(换元必换限)； (2) 求出 f [(t)] (t) 的一个原函数(t) 后，不需代回 原来的变量，直接计算() - () 即可. (3) 换元公式相当于不定积分的第二换元积分法，反 过来用换元公式即为凑微分法，用凑微分法能直接算出 原函数时，可以不换元

第三节定积分的换元法和分部积分法 例1计算心Va2-x2d(a>0) y=Va2-x2 解 例2计算2 cosxsin xdx 解 X 例3计算vsin3x-sn5xdk 解 上页 下页 返回 MathGS 公式 线与面 数学家

第三节 定积分的换元法和分部积分法 例1 计算 d ( 0). 0 2 2 −   a x x a a 第三节 定积分的换元法和分部积分法 解 例1 计算 d ( 0). 0 2 2 −   a x x a a 令 x = a sin t，则 dx = a cos t dt， 当 x = 0 时，取 t = 0; 当 x = a 时，取 t = /2 . 于是  − a a x x 0 2 2 d  = 2 π 0 2 2 a cos t dt  = + 2 π 0 2 (1 cos 2 ) d 2 t t a 2 π 0 2 sin 2 2 1 2       = t + t a . 4 π 2 a = 例2 计算 cos sin d . 2 π 0 5  x x x 第三节 定积分的换元法和分部积分法 解 例2 计算 cos sin d . 2 π 0 5  x x x  2 π 0 5 cos xsin xdx  = 2 π 0 5 cos xd cos x 不作变量代换 2 π 0 cos 6 1       = x . 6 1 = 作变量代换 令 t = cos x , 则 dt = -sin x dx , 且 当 x = 0 时，t = 1; 当 x = /2 时，t = 0 . 于是  2 π 0 5 cos xsin xdx  = − 0 1 5 t dt  = 1 0 5 t dt . 6 1 = 例3 计算 sin sin d . π 0 3 5  x − x x 第三节 定积分的换元法和分部积分法 解 例3 计算 sin sin d . π 0 3 5  x − x x 由于 x x 3 5 sin −sin sin | cos | , 2 3 = x x  − π 0 3 5 sin x sin x dx   =  +  π 2 π 2 3 2 π 0 2 3 sin x | cos x | dx sin x | cos x | dx   =  −  π 2 π 2 3 2 π 0 2 3 sin x cos x dx sin x cos x dx 所以 π 2 π 2 5 2 π 0 2 5 sin 5 2 sin 5 2        −      = x x . 5 4 = a a 2 2 y = a − x x y O

第三节定积分的换元法和分部积分法 例4计算 X+2 dx 解 例5证明： ()若fx)在【-，上连续且为偶函数，则 f(x)dx=2f(x)dx. (2)若fx)在【-M,上连续且为奇函数，则 巴faw)dr=0 证明 上页 下页 返回 MathGS 公式 线与面 数学家

第三节 定积分的换元法和分部积分法 例4 计算 d . 2 1 4 2 0 + + x x x 第三节 定积分的换元法和分部积分法 解 例4 计算 d . 2 1 4 2 0 + + x x x 设 2x +1 = t , 则 , d d , 2 1 2 x t t t x = − = 且 当 x = 0 时，t = 1 ; 当 x = 4 时，t = 3 . 于是  + 4 + 0 d 2 1 2 x x x  + − = 3 1 2 d 2 2 1 t t t t  = + 3 1 2 ( 3) d 2 1 t t 3 1 3 3 2 3 1       = + t t . 3 22 = 例5 证明: ( ) d 2 ( ) d .  0 = − a a a f x x f x x 第三节 定积分的换元法和分部积分法 证明 ( ) d 2 ( ) d .  0 = − a a a f x x f x x ( ) d = 0 . − a a f x x 当 f(x) 为偶函数时 当 f(x) 为奇函数时 因为 ( ) d ( ) d ( ) d , 0 0    = + − − a a a a f x x f x x f x x 对积分 − 0 ( ) d a f x x 作变量代换 x = - t，则得 − 0 ( ) d a f x x  = − − 0 ( ) d a f t t ( ) d . 0 = − a f x x 所以 ( ) d [ ( ) ( )] d .  0 = + − − a a a f x x f x f x x (1) 若 f (x) 在 [-a , a] 上连续且为偶函数，则 ( ) d = 0 . − a a f x x (2) 若 f (x) 在 [-a , a] 上连续且为奇函数，则

第三节定积分的换元法和分部积分法 例6若fx)在0,1川上连续，证明 (1)f(sin x)dx=fcsx)dx; (2)(sin x)dx=f(si x)dx. 并由此计算 xsin x dx. 证明 上页 下页 返回 MathGS 公式 线与面 数学家

第三节 定积分的换元法和分部积分法 例6 若 f (x) 在 [0 , 1] 上连续，证明 (sin ) d , 2 π (2) (sin ) d (1) (sin ) d (cos ) d ; π 0 π 0 2 π 0 2 π 0     = = x f x x f x x f x x f x x 第三节 定积分的换元法和分部积分法 证明 (sin ) d , 2 π (2) (sin ) d (1) (sin ) d (cos ) d ; π 0 π 0 2 π 0 2 π 0     = = x f x x f x x f x x f x x d . 1 cos π sin 0 + x x x x 计算 (1) 令 , 2 π x = − t 则  2 π 0 f (sin x) dx              = − − 0 2 π d 2 π f sin t t  = 2 π 0 f (cost) dt (cos ) d . 2 π 0 = f x x d . 1 cos π sin 0 + x x x x 并由此计算

第三节定积分的换元法和分部积分法 例7设fx)是周期为T的周期函数，证明 ④afa)dr=fx)d; (2)f()dnf()d (nN) 并由此计算 I +sin 2x dx. 证明 上页 下页 返回 MathGS 公式 线与面 数学家

第三节 定积分的换元法和分部积分法 例7 设 f (x) 是周期为T 的周期函数，证明 (2) ( ) d ( ) d ( N), (1) ( ) d ( ) d ; 0 0 =  =     + + f x x n f x x n f x x f x x a n T T a a T T a 第三节 定积分的换元法和分部积分法 证明 (1) 令 (2) ( ) d ( ) d ( N), (1) ( ) d ( ) d ; 0 0 =  =     + + f x x n f x x n f x x f x x a n T T a a T T a 1 sin 2 d . π 0 + n 计算 x x ( ) ( ) d ,  + = a T a Φ a f x x 则 Φ(a) = f (a +T) − f (a) = 0 , 由此可知，(a) 与 a 无关，因此(a) = (0) ，即 ( ) d ( ) d .  0 = a+T T a f x x f x x 1 sin 2 d . π 0 + n 并由此计算 x x

第三节定积分的换元法和分部积分法 例8计算 6x-3x+3 ,dx. 解之 x≥0， 例9设f(x)= 1,-<x< 计算广f(x-2r 1+cosx 解 上页 下页 返回 MathS 公式 线与面 数学家

第三节 定积分的换元法和分部积分法 例8 计算 d . ( 3 3) 3 0 2 2 2 x x x x  − + 第三节 定积分的换元法和分部积分法 解 例8 计算 d . ( 3 3) 3 0 2 2 2 x x x x  − + , 4 3 2 3 3 3 2 2  +      x − x + = x − 令 ) , 2 π tan (| | 2 3 2 3 x − = u u  则 sec , 16 9 ( 3 3) 2 2 4 x − x + = u sec d . 2 3 d 2 x = u u 且当 x = 0 时， ; 3 π u = − 当 x = 3 时， . 3 π u = 例9 设      −   +  = − , π 0 , 1 cos 1 e , 0 , ( ) 2 x x x x f x x 第三节 定积分的换元法和分部积分法 解 例9 设      −   +  = − , π 0 , 1 cos 1 e , 0 , ( ) 2 x x x x f x x 计算 ( 2)d . 4 1 f x x  − 设 x – 2 = t ，则 dx = dt，且 当 x = 1 时，t = -1 ; 当 x = 4 时，t = 2 . 于是 f (x 2)dx 4 1 − f (t)dt 2 −1 = t t t t t d e d 1 cos 1 2 0 0 1 2   − − + + = 2 0 0 1 2 e 2 1 2 tan       −       = − − t t . 2 1 e 2 1 2 1 tan 4 = − + − 计算 ( 2)d . 4 1 f x x  −

第三节定积分的换元法和分部积分法 二、定积分的分部积分法 不定积分的分部积分法∫dv=w-∫d 定积分的分部积分法心wdv=wl上-心du 上页 下页 返回 MathGS 公式 线与面 数学家

第三节 定积分的换元法和分部积分法 二、定积分的分部积分法 不定积分的分部积分法 udv uv vdu   = − 定积分的分部积分法 u v uv v u b a b a b a d d   = −

第三节定积分的换元法和分部积分法 例10计算2 arcsin xdx 解 例11计算ed 解 上页 下页 返回 MathGS 公式 线与面 数学家

第三节 定积分的换元法和分部积分法 例10 计算 arcsin d . 2 1 0 x x  第三节 定积分的换元法和分部积分法 解 例10 计算 arcsin d . 2 1 0 x x  arcsin xdx 2 1 0   x x x x x d 1 arcsin 2 1 0 2 2 1 0  − = −   2 1 0 2 1 6 π 2 1 =  + − x 1. 2 3 12 π = + − 例11计算 e d . 1 0 x x  第三节 定积分的换元法和分部积分法 解 例11 计算 e d . 1 0 x x  先用换元法. 令 x = t , 则 x = t 2 , dx = 2tdt , 当 x = 0 时， t = 0 ; 当 x = 1 时， t = 1 . 于是 e x x d 1 0 t t t 2 e d 1 0 = t 2 tde 1 0 = t t t t 2[ e ] 2 e d 1 0 1 0  = − 1 0 2e 2[e ] t = − = 2