《高等数学》课程教学资源（PPT课件）第七章微分方程_第七节常系数齐次线性微分方程

第七节常系数齐次线性微分方程 一、定义 二、解法 三、举例 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 常系数齐次线性微分方程 一、定义 二、解法 三、举例

第七节常系数齐次线性微分方程 定义 定义形如 J”+y+心=0(p,q是常数) 的方程称为二阶常系数齐次线性微分方程，如果p,q不 全是常数，则称之为二阶变系数齐次线性微分方程 例如，J”+2y-5y=0,二阶常系数齐次线性微分方程 y”+2y'+3xy=0.二阶变系数齐次线性微分方程 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 常系数齐次线性微分方程 一、 定义 定义 形如 y + py + qy = 0 (p , q 是常数) 的方程称为二阶常系数齐次线性微分方程，如果 p , q 不 全是常数，则称之为二阶变系数齐次线性微分方程. 例如，y + 2y – 5y = 0, 二阶常系数齐次线性微分方程 y + 2y + 3xy = 0. 二阶变系数齐次线性微分方程

第七节常系数齐次线性微分方程 二 解法 1.二阶常系数齐次线性微分方程 由二阶齐次线性微分方程通解的结构可知，要求通 解，就是要求它的两个线性无关的特解.那么如何求两 个线性无关的特解呢？为此先来分析方程的特点. 特点函数与其一阶、二阶导数只差一个常数因子. 而指数函数y=ex(r为常数)刚好具有这一特性， 因此可用指数函数y=ex(r为常数)来尝试， 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 常系数齐次线性微分方程 由二阶齐次线性微分方程通解的结构可知，要求通 解，就是要求它的两个线性无关的特解. 那么如何求两 个线性无关的特解呢？为此先来分析方程的特点. 特点 函数与其一阶、二阶导数只差一个常数因子. 而指数函数 y = erx (r 为常数) 刚好具有这一特性， 因此可用指数函数 y = erx (r 为常数) 来尝试. 二、 解法 1. 二阶常系数齐次线性微分方程

第七节常系数齐次线性微分方程 J”+y+y=0D,q是常数) 设y=er(r为待定常数)是方程的解，则 y'=rerx,y"=r2erx, 代入方程并化简，得 (r2+pr+g)erx=0. 0 特征方程 r2+pr+q=0. 这就说明：只要r满足特征方程，那么y=ex便是解 上页 下页 返回 MathGS 公式 线与面 数学家

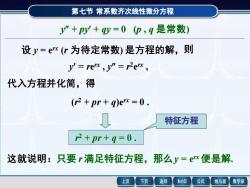
第七节 常系数齐次线性微分方程 y + py + qy = 0 (p , q 是常数) 设 y = erx (r 为待定常数) 是方程的解，则 y = re rx , y = r2e rx , 代入方程并化简，得 (r 2 + pr + q)erx = 0 . r 2 + pr + q = 0 . 特征方程 这就说明：只要 r 满足特征方程，那么 y = erx 便是解

第七节常系数齐次线性微分方程 y”"+py+y=0p,q是常数)2+pr+q=0 1.当p2-4q>0时，特征方程有两个不相等的实根 设为，2，则可得微分方程的两个线性无关的特解： y=eix,y2=ex 于是通解为 y=Cen+Ce 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 常系数齐次线性微分方程 y + py + qy = 0 (p , q 是常数) r 2 + pr + q = 0 1. 当 p 2 – 4q > 0 时，特征方程有两个不相等的实根 设为 r1 , r2 , 则可得微分方程的两个线性无关的特解： e , e , 1 2 1 2 r x r x y = y = 于是通解为 e e . 1 2 1 2 r x r x y = C + C

第七节常系数齐次线性微分方程 y”+py+y=0p,q是常数)2+pr+q=0 2.当p2-4q=0时，特征方程只有一个实根设为r, 这时只能得一个特解y=e.下面用常数变易法再求 一个与y1线性无关的特解.设y2=xy1=ux)ex是 一个解，代入方程并化简，得 e[m"+(2r+p)d+(r2+pr+q)l=0. 由于r是特征方程的二重根，故上述方程即为”=0. 取u=x,则2=xex.于是通解为y=(C1+C2x)e 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 常系数齐次线性微分方程 y + py + qy = 0 (p , q 是常数) r 2 + pr + q = 0 2. 当 p 2 – 4q = 0 时，特征方程只有一个实根设为 r， 这时只能得一个特解 e . 1 rx y = 一个与 y1 线性无关的特解. 下面用常数变易法再求 设 y2 = u(x)y1 = u(x)erx 是 一个解，代入方程并化简，得 e [ (2 ) ( ) ] 0 . 2 u + r + p u + r + pr + q u = r x 由于 r 是特征方程的二重根，故上述方程即为 u  = 0 . 取 u = x ，则 y2 = xe rx . 于是通解为 ( )e . 1 2 rx y = C + C x

第七节常系数齐次线性微分方程 ”+py+=0D,q是常数) 2+p+q=0 3.当p2-4q<0时，特征方程有一对共轭复根 n=a+iB,r=a-iB. 这时原方程有两个复数解： (iB)=ex(cosBx+isin Bx), v2=c(-i)xeax(cos Bx-isin Bx). 利用解的叠加原理，得原方程的线性无关特解： 4=2(0h+y2)=ea"c0sBx, 2=(4-2)=eas sin Bx. 上项 下页 返回 MathGS 公式 线与面 数学家

第七节 常系数齐次线性微分方程 y + py + qy = 0 (p , q 是常数) r 2 + pr + q = 0 3. 当 p 2 – 4q < 0 时，特征方程有一对共轭复根 这时原方程有两个复数解: x y ( i ) 1 e +  = e (cos x isin x ) , x    = + x y ( i ) 2 e −  = e (cos x isin x ). x    = − ( ) 2 1 2 1 1 y = y + y ( ) 2 i 1 2 1 2 y = y − y e cos x , x   = e sin x . x   = 利用解的叠加原理 , 得原方程的线性无关特解:

第七节常系数齐次线性微分方程 y"+py+y=0p,q是常数)2+pr+q=0 于是通解为 y=ex(C CosBx+C2sin Bx). 综上所述，可得求通解的步骤： Step1写出特征方程； Step2求出特征方程的两个根； Step3根据特征方程的两个根的不同情形写出通解. 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 常系数齐次线性微分方程 于是通解为 e ( cos sin ). 1 2 y C x C x x    = + 综上所述，可得求通解的步骤： Step1 写出特征方程； Step2 求出特征方程的两个根； Step3 根据特征方程的两个根的不同情形写出通解. y + py + qy = 0 (p , q 是常数) r 2 + pr + q = 0

第七节常系数齐次线性微分方程 y”"+py+心=0p,q是常数)2+pr+q=0 特征方程的两个根 通解 两个实根”1≠2 y=Cex+C,ex 两个实根r1=2=r y=(C+C2x)e 两个复根r12=a士邛 y=(C COs B+C2 sin Bx)ec 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 常系数齐次线性微分方程 特征方程的两个根 通解 两个实根 r1  r2 r x r x y C 1 C 2 e e = 1 + 2 两个实根 r1 = r2 = r rx y (C C x)e = 1 + 2 两个复根 r1,2 =   i x y C C x  ( cos  sin  )e = 1 + 2 y + py + qy = 0 (p , q 是常数) r 2 + pr + q = 0

第七节常系数齐次线性微分方程 2.n阶常系数齐次线性微分方程 n阶常系数齐次线性微分方程的一般形式是 ym）+p1ym-l+p2Jym-2)+.+Pn-1y'+pny=0, 其中p1,P2,.,Pn都是常数. 其特征方程为 rn+pirmI+parm2+.+pnir+en=0. 特征方程是一元n次方程，在复数范围内有n个根，k 重根算k个根.根据特征根可以写出其对应的微分方程 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 常系数齐次线性微分方程 2. n 阶常系数齐次线性微分方程 n 阶常系数齐次线性微分方程的一般形式是 y (n) + p1 y (n-1) + p2 y (n-2) + . + pn-1 y + pn y = 0, 其中 p1 , p2 , . , pn 都是常数. 其特征方程为 r n + p1 r n-1 + p2 r n-2 + . + pn-1 r + pn = 0 . 特征方程是一元 n 次方程，在复数范围内有 n 个根，k 重根算 k 个根. 根据特征根可以写出其对应的微分方程