《线性代数》课程教学课件（讲稿，B）矩阵的秩

§2.4矩阵的秩 一、矩阵的行（列秩、秩 二、矩阵秩与向量组的极大 无关组、秩的求法 三、矩阵秩的第二定义 四、小结

§2.4 矩阵的秩 一、 矩阵的行(列)秩、秩 三、矩阵秩的第二定义 四、小结 二、 矩阵秩与向量组的极大 无关组、秩的求法

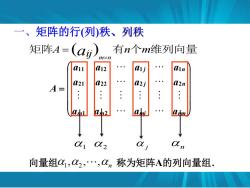
矩阵的行（列秩、列秩 矩阵A=(a可) 有n个m维列向量 xn 11 L12 L21 L22 a2n A= .: L2 n 向量组C1,C2,.,C,称为矩阵A的列向量组

矩阵A aij 有n个m维列向量 m n ( )                  a a a a a a a a a a a a A m m mj mn j n j n             1 2 2 1 2 2 2 2 1 1 1 2 1 1 1  2  j  n 一、矩阵的行(列)秩、列秩 向量组  1 ,2 ,  , n 称为矩阵A的列向量组．

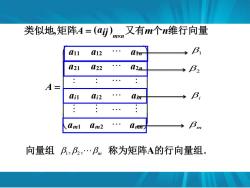
类似地，矩阵A=(uj,又有m个n维行向量 11 L12 L21 L22 a2n B. A= Ail Ai2 lin B, Am1 am2 (Lmn Bm 向量组乃，B2,.Bm称为矩阵A的行向量组

类似地,矩阵A  (aij) mn 又有m个n维行向量                    a a a a a a a a a a a a A m m mn i i in n n             1 2 1 2 21 22 2 11 12 1 1  2  i  m 向量组 1 ,2 ,  m 称为矩阵A的行向量组．

1.定义2.4.1设m×n矩阵A,称A的行向量组的秩称 为矩阵A的行秩，列向量组的秩称为矩阵A的列秩 10 例题1：求矩阵A= 012的行秩和列秩 214 解：4A的行向量1=(1,0,1)，2=(0,1,2)，43=(2,1,4) 101 由行列式012=0，知向量组，2，a,线性相关， 214

1.定义2.4.1 设m×n矩阵A，称A 的行向量组的秩称 为矩阵A的行秩，列向量组的秩称为矩阵A的列秩. 1 2 3 A的行向量      (1,0,1), (0,1,2), (2,1,4) 1 2 3 1 0 1 0 1 2 0 , , 2 1 4 由行列式  ，知向量组   线性相关， 解： . 2 1 4 0 1 2 1 0 1 例题1:求矩阵 的行秩和列秩           A 

又a1,a,线性无关，故a,是4的行向量组的一个 最大无关组，所以矩阵A的行秩等于2. 同样方法可以求出A的列秩等于2. 1131 例题2：求矩阵A=02-14的行秩和列秩 0005 解：A的三个行向量为 1=(1,1,3,1),c2=(0,2,-1,4),C3=(0,0,0,5) 去掉A的第三个分量量 a=(1,1,1),=(0,2,4),4g=(0,0,5

1 2 1 2 , , 2. A A 又    线性无关，故 是 的行向量组的一个 最大无关组，所以矩阵 的行秩等于 1 2 3        (1,1,3,1), (0,2, 1,4), (0,0,0,5). 同样方法可以求出A的列秩等于2. 解：A的三个行向量为 1 2 3          (1,1,1), (0,2,4), (0,0,5). . 0 0 0 5 0 2 1 4 1 1 3 1 例题2 :求矩阵 的行秩和列秩           A   去掉A的第三个分量量

111 由行列式024=10≠0，知向量组a,a,线性无关 005 由S2.3例5知，向量组a%1,2,c也线性无关， 所以A的行秩为3. 11 1 3 11 的列向量组B, = 0 829 B= 4 5 4个三维向量必线性相关，而其中BBB,线性无关

1 2 3 111 0 2 4 10 0 , , 005 由行列式   ，知向量组     线性无关. § 1 2 3 2.3 5 , , A 3. 由 例 知，向量组   也线性无关， 所以 的行秩为 1 2 3 4 1 1 3 1 0 2 1 4 0 0 0 5 A                                                  的列向量组 4个三维向量必线性相关，而其中β1β2β4线性无关

因为 1 0 0 12 0=10≠0 1 45 所以A的列秩也等于3. 例1和例2中矩阵的行秩等于列秩并非是偶然的.为了 证明这一点，我们有以下两个定理， 2.矩阵的初等行列变换矩阵的行列秩的影响。 定理2.4.1初等行（列）变换不改变矩阵的行（列秩. 证明：此处只就第三种初等行变换不改变矩阵的 行秩证明之，其余两种课下自己来完成

1 0 0 1 2 0 10 0 1 4 5   因为 所以A的列秩也等于3. 例1和例2中矩阵的行秩等于列秩并非是偶然的.为了 证明这一点,我们有以下两个定理. 定理2.4.1 初等行(列)变换不改变矩阵的行(列)秩. 证明： 此处只就第三种初等行变换不改变矩阵的 行秩证明之，其余两种课下自己来完成. 2.矩阵的初等行列变换对矩阵的行(列)秩的影响

设m×矩阵4的行向量组c4,a2,.,&m且 a a c a;+kaj n+krj A- .号 =B ai Cm」 Cm

1 2 , , 设m n A  矩阵 的行向量组   ， m ，且 1 1 ~ i j i j i r kr j j m m k A B                                                               

由 01=01 a;=(a;+ka;)-kaj 0。·。 dm=am 可知，矩阵A的行向量组可由B的行向量组线性表示. 显然，矩阵B的行向量组可由A的行向量组线性 表示.所以，矩阵A、B的行向量组等价.从而矩阵A、 B的行向量组的秩相同

1 1 ( ) i i j j m m k k              由 可知，矩阵A的行向量组可由B的行向量组线性表示. 显然，矩阵B的行向量组可由A的行向量组线性 表示.所以，矩阵A、B的行向量组等价.从而矩阵A、 B的行向量组的秩相同

同样的方式可证明对矩阵做一次第二第三种类型 的初等行变换，可得到矩阵的行秩也相等。 定理2.4.1对应到化简线性方程组上即为初等变换不 改变线性方程组中独立方程的个数。 定理2.4.2初等行（列变换不改变矩阵列（行）向量间 的线性关系. A=[a,a2,.,an]→[B,B2,.,Bn]=B 则有x,1+x202+.+Xnn=0 当且仅当xB,+x2B2+.+xnBn=0

定理2.4.1对应到化简线性方程组上即为初等变换不 改变线性方程组中独立方程的个数。 定理2.4.2 初等行(列)变换不改变矩阵列(行)向量间 的线性关系. A  1 ,2 ,  ,n 1 ,2 ,  ,n  B 则有x1 1  x2 2  xn n  0 当且仅当x11  x2 2  xn n  0 同样的方式可证明对矩阵做一次第二第三种类型 的初等行变换，可得到矩阵的行秩也相等