《线性代数》课程教学资源（PPT讲稿，C）3-3初等矩阵

第 三 节 初 等 矩 阵 1 上页

第三节 初 等 矩 阵

课前复习 矩阵的初等变换(Elementary transformation) (c,c): 初等行（列）变换5×k(c:×k); 5+(c+kc,) 2、子式与阶子式 3、秩的定义及性质 in Aun,f(1)3D,≠0；（2)VD+1=0. 则称为矩阵的最高阶非零子式. 最高阶非零子式 的阶数称为矩阵的秩，记为r(或 R(A 上页

２、子式与 k 阶子式 ３、秩的定义及性质 课前复习 １、矩阵的初等变换（Elementary transformation） 初等行(列)变换 ( ) ; i j i j r r c c   ( ) ; i i r k c k   ( ) . i j i j  r kr c kc + +       , m n in A if  0 ;   D r 1 0 . （1） （2）  = D r+ 则 称为矩阵 的最高阶非零子式. D r A 记为 r(A或) R. (A) 最高阶非零子式 的阶数称为矩阵的秩

4、如果矩阵A经过有限次初等变换变成矩阵B, 就称矩阵A与B等价，记作A~B 5、利用初等行变换可把矩阵化为行阶梯形矩阵！ 利用初等行变换，也可把矩阵化为行最简形矩阵， 利用初等行变换，再利用初等列变换最后可把矩阵 化为标准形矩阵。 最高阶非零子式的阶数 6、矩阵的秩 行阶梯形矩阵非零行的行数 行最简形矩阵非零行的行数 标准形矩阵中单位矩阵的阶数

４、如果矩阵 A 经过有限次初等变换变成矩阵 B ， 就称矩阵 A B 与 等价 ，记作 A B~ 利用初等行变换可把矩阵 A 化为行阶梯形矩阵. 利用初等行变换，也可把矩阵化为行最简形矩阵. 5、 利用初等行变换，再利用初等列变换最后可把矩阵 化为标准形矩阵. 6、矩阵的秩 = 最高阶非零子式的阶数 = 行阶梯形矩阵非零行的行数 = 行最简形矩阵非零行的行数 = 标准形矩阵中单位矩阵的阶数 

、初等矩阵的概念 矩阵的初等变换是矩阵的一种基本运算，应 用广泛. 定义由单位矩阵E经过一次初等变换得到的方 阵称为初等矩阵.E→P, 三种初等变换对应着三种初等方阵， 1.对调两行或两列； 2.以数k≠0乘某行或某列； 3.以数k乘某行（列）加到另一行（列)上去

定义 由单位矩阵 经过一次初等变换得到的方 阵称为初等矩阵. E 三种初等变换对应着三种初等方阵. 矩阵的初等变换是矩阵的一种基本运算，应 用广泛. 一、初等矩阵的概念       以数 乘某行（列）加到另一行（列）上去． 以数 乘某行或某列； 对调两行或两列； k k 3. 2. 0 1. , ET E P ⎯⎯⎯→ 一次

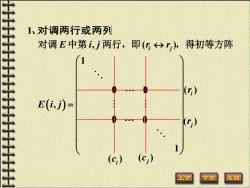
1、对调两行或两列 对调E中第i,j两行，即(G→)，得初等方阵 1 ) E(i,)= (c) (C) 上页

对调 E 中第 i, j 两行，即(ri  rj )，得初等方阵 1、对调两行或两列 ( ) 1 1 0 , 0 1 1 E i j           =           0 1 1 0 ( )i r ( )j r ( )j ( ) c i c

2 3 1 E,(2,3)A= 123 13 = 为 4 2 1 100 AE,(2,3)= = 上页 返回

1 0 0 0 0 1 0 1 0           1 2 3 2 2 1 3 4 3           1 2 3 3 4 3 2 2 1     =       3 E A (2,3) = 3 AE (2,3) = 1 2 3 2 2 1 3 4 3           1 0 0 0 0 1 0 1 0           1 3 2 2 1 2 3 3 4     =      

用m阶初等矩阵Enm(i,j)左乘A=(a)nxn,得 相当于对矩阵A施行第一种初等行变换： 把A的第i行与第j行对调（→） L11 12 n 02. m ←-第i行 Em(i,j)A= 几 ai2 L 第j行

用m 阶初等矩阵Em (i, j) 左乘 A = (aij)mn，得                       = m m mn i i in j j jn n m a a a a a a a a a a a a E i j A              1 2 1 2 1 2 1 1 1 2 1 ( , )  第 i 行  第 j 行 ( ). i j A i j r r A 把 的第 行与第 行对调  相当于对矩阵 施行第一种初等行变换：

类似地， 以n阶初等矩阵En(i,j)右乘矩阵A, 相当于对矩阵A施行第一种初等列变换： 把A的第i列与第j列对调(c,)c): 1 (Ti n AE,(i,j)= 区回

以 阶初等矩阵 右乘矩阵 ， 类似地， n En (i, j) A               = m mj mi mn j i n j i n n a a a a a a a a a a a a AE i j              1 2 1 2 2 2 1 1 1 1 1 ( , ) ( ). i j A i j c c A 把 的第 列与第 列对调  相当于对矩阵 施行第一种初等列变换：

2、以数k≠0乘某行或某列 以数k≠0乘单位矩阵的第行(y×k),得初等 矩阵E(i(k) E(i(k))= ←第i行 上页

2、以数 k  0 乘某行或某列 ( ( )). 0 ( ) E i k k i ri k 矩阵 以数  乘单位矩阵的第 行  ，得初等                       = 1 1 1 1 ( ( ))   E i k k  第 i 行

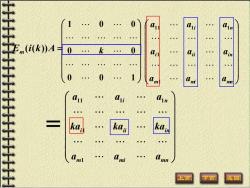
1 0 0 i (i(k))A= 0 0 0 0 i ka: Ami 上页 返回

11 1 1 1 1 i n i ii in m mi mn a a a ka ka ka a a a               ( ( )) E i k A m =                 0 0 1 0 0 1 0 0                 k                 m mi mn i i i i n i n a a a a a a a a a                 1 1 11 1 1 =