《概率论与数理统计》课程教学课件（习题课，PPT）第三章 多维随机变量及其分布

概车纶与款理统外 第三章 多维随机变量及其分布 习题课 一、重点与难点 二、主要内容 三、典型例题

一、重点与难点 二、主要内容 三、典型例题 第三章 多维随机变量及其分布 习 题 课

概率伦与款程统外 一、重点与难点 1.重点 二维随机变量的分布 有关概率的计算和随机变量的独立性 2.难点 条件概率分布 随机变量函数的分布

一、重点与难点 1.重点 二维随机变量的分布 有关概率的计算和随机变量的独立性 2.难点 条件概率分布 随机变量函数的分布

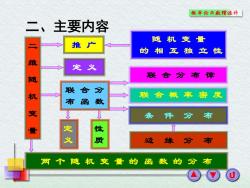
概车纶与款理统外 二、主要内容 随机变量 二 推 的相互独立性 维 定义 随 联合分布律 联 合 分 机 联合概率密度 布函 数 变 条件 分布 定 性 义 质 边 缘分布 两个随机变量的函数的分布

定 义 联 合 分 布 函 数 联 合 分 布 律 联 合 概 率 密 度 边 缘 分 布 条 件 分 布 两 个 随 机 变 量 的 函 数 的 分 布 随 机 变 量 的 相 互 独 立 性 定 义 性 质 二 维 随 机 变 量 推 广 二、主要内容

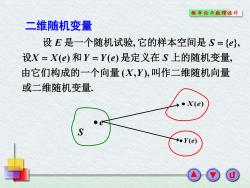
概華论与款醒硫外「 二维随机变量 设E是一个随机试验，它的样本空间是S={, 设X=X(e)和Y=Y(e)是定义在S上的随机变量， 由它们构成的一个向量(X,),叫作二维随机向量 或二维随机变量. ●X(e) →eY(e)

. ( , ), ( ) ( ) , , { }, 或二维随机变量 由它们构成的一个向量 叫作二维随机向量 设 和 是定义在 上的随机变量 设 是一个随机试验 它的样本空间是 X Y X X e Y Y e S E S e = = = 二维随机变量 • e •Y(e) S • X(e)

概车纶与款理统外 二维随机变量的分布函数 F(x,y)=P{(X≤x)∩(Y≤y)}=P{X≤x,Y≤y}

F(x, y) = P{(X  x)(Y  y)} = P{X  x,Y  y} 二维随机变量的分布函数

概華伦与款程统外 二维离散型随机变量的分布律 P{X=x,Y=y}=p,i,j=1,2,., X1 X2 Xi y P11 P21 Pn y2 P12 P22 Pi 必

P{X = x , Y = y } = p , i, j =1,2,  , i j i j 二维离散型随机变量的分布律 X Y x1 x2  xi    j y y y 2 1 p11 p21  pi1  p12 p22  pi 2     p1 j p2 j  pij    

概车纶与款理统外 二维连续型随机变量的概率密度 F(x,y)=广nf(,)dudy, f(x.y)dxdy=F(c.)=1. P(X,r)eG}=∬fx,)drd

F(x, y) f (u,v) du dv, y x − − = 二维连续型随机变量的概率密度 ( , ) d d = (,) =1.   + − + − f x y x y F {( , ) } ( , ) d d .   = G P X Y G f x y x y

概率伦与款程统外 离散型随机变量的边缘分布律 设二维离散随机变量(X,Y)的联合分布律为 P{X=x,Y=yj}=p,i,j=1,2,. 记 p-∑P=P{X=x,i=l,2, p=∑Pg=PY=y,j=12, 分别称p.(i=1,2,)和p(0=1,2,)为(X,Y) 关于X和关于Y的边缘分布律

. ( 1,2, ) ( 1,2, ) ( , ) { }, 1,2, , { }, 1,2, , { , } , , 1,2, . ( , ) 1 1 关于 和关于 的边缘分布律 分别称 和 为 记 设二维离散随机变量 的联合分布律为 X Y p i p j X Y p p P Y y j p p P X x i P X x Y y p i j X Y i j j i j ij i j i ij i j ij      = = = = = = = = = = = = = = • •  = •  = •   离散型随机变量的边缘分布律

想率纶与敲程统科「 连续型随机变量的边缘概率密度 fx(x)=」nf(x,y)dy f(y)=[f(x,y)dx

连续型随机变量的边缘概率密度 ( ) ( , )d .  + − f y = f x y x Y ( ) ( , )d .  + − f x = f x y y X

概率伦与款程统外 随机变量的条件分布 (1)离散型随机变量的条件分布 设(X,Y)是二维离散型随机变量，对于固定的 j,若P{Y=}>0,则称 P(X-XY-)-PX-XY-y P(Y=y} P.j i=1,2,. 为在Y=y条件下随机变量X的条件分布律

. 1,2, , , { } { , } { } , { } 0, ( , ) , 为在 条件下随机变量 的条件分布律 若 则称 设 是二维离散型随机变量 对于固定的 Y y X i p p P Y y P X x Y y P X x Y y j P Y j X Y j j ij j i j i j = = = = = = = = = =  •  (1) 离散型随机变量的条件分布 随机变量的条件分布