《线性代数》课程教学资源（PPT讲稿，C）4-2齐次线性方程组

第二节齐线性方程组 上页

第二节 齐线性方程组

二、 齐次线性方程组解的性质 1、 解向量设有齐次线性方程组 011x1+412x2+.+1mXn=0 L21x1+2X2+.+L2mXn=0 (1) mlxi+m2x2+.+AmXn=0 11 12 若记A= L21 L22 a2n x= m2 则上述方程组(1)可写成矩阵方程Ax=0. 返回

１、解向量 设有齐次线性方程组 11 1 12 2 1 21 1 22 2 2 1 1 2 2 0 0 0 n n n n m m mn n a x a x a x a x a x a x a x a x a x  + + + =   + + + =    + + + =  若记 （1） 一、齐次线性方程组解的性质 11 12 1 21 22 2 1 2 , n n m m mn a a a a a a A a a a     =                       = n x x x x  2 1 则上述方程组（1）可写成矩阵方程 Ax = 0

若x1=51,x2=51,.,xn=5n1 使得方程x=成立， 主主王王王王王 5 则 51 x= 称为方程组（1)的解向量 它也就是矩阵方程Ax=0的解. 齐次线性方程组解的性质 (1若51，x2=约Ax的解，则 x=51+52 也是Ax的解， (2)若x1为的解， 为实数，则 x=kg 也是x=的解 易知，方程组的全体解向量构成一个向量空间 称此向量空间为齐次线性方程组Ax 0的解空间

1 11 2 21 1 , , , n n 若 x x x = = =    11 21 n1 x        =         称为方程组（1）的解向量， ２、齐次线性方程组解的性质 （1）若 x x 1 1 2 2 = =   , 为 Ax 的解，则 = 0 x =  1 +  2 也是 Ax = 的解 0 . （2）若 x1 1 = 为  Ax 的解， = 0 为实数，则 k x = k 1 也是 Ax = 的解． 0 称此向量空间为齐次线性方程组 Ax = 0的解空间． 易知，方程组的全体解向量构成一个向量空间， 则 使得方程 Ax = 0 成立， 它也就是矩阵方程 Ax = 0 的解．

解空间的基础解系及其求法 1、基础解系的定义 设51,52，.，5m-,是AX=0的解，满足 (1)51,52,.,5m,线性无关 (2)Ax=0的任一解都可以由51,52，.，5m, 线性表示。 则称51,52，5n,是A化=0的一个基础解系。 如果51,52，.，5，为齐次线性方程组Ax=0的 基础解系，则方程组Ax=0的通解可表示为： 王王王 x=k151+k252+.+k,5) 其中k1,k2,.,k,为任意实数

二、解空间的基础解系及其求法 设 1 2 , , , n r    − 是 AX = 0 的解，满足 1 2 1 , , , n r    （ ） − 线性无关； （2 0 ）Ax = 的任一解都可以由 1 2 , , , n r    − 线性表示。 则称 1 2 , , , n r    − 是 Ax = 0 的一个基础解系。 １、基础解系的定义 基础解系，则方程组 Ax = 0 的通解可表示为： 如果    1 2 , , , s 为齐次线性方程组 Ax = 0 的 1 1 2 2 , s s x k k k = + + +    其中 为任意实数. 1 2 , , , s k k k

2、 求基础解系的步骤： 1、 对系数矩阵A进行初等变换，将其化为最简形 1 0-b1 00 1 A~ -br br.n . 0 . . 0 则 R(A)=r 上页

11 1, 1 , 1 0 - - 0 1 - - ~ 0 0 0 0 n r r r n r b b b b A − −       １、对系数矩阵Ａ进行初等变换，将其化为最简形 R(A) = r 2、求基础解系的步骤: 则

0 -bu . -b1- 由于 0 .1 A- -br . -b- 0 0 0 0 所以 x1=bx,+1+b2x,+2+.+bm-xn 4x=0→ (2) x,=b1+1+b2x+2++bm-xn 其中x+1,x,+2,x。是任意实数称为自由未知量。 区回

11 1, 1 , 1 0 - - 0 1 - - ~ 0 0 0 0 n r r r n r b b b b A − −       （２） 1 11 1 12 2 1, 1 1 2 2 , 0 r r n r n r r r r r r n r n x b x b x b x Ax x b x b x b x + + − + + −  = + + +  =    = + + +  所以 由于 其中 1 2 , , , x x x r r n + + 是任意实数.称为自由未知量

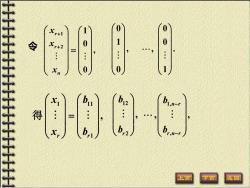
令 10:0 , 01:0 00:1 得 上页 下页

令 1 2 1 0 , 0 r r n x x x + +             =             1 11 1 , r r x b x b         =             得 0 1 , 0             0 0 , . 1             12 2 , r b b           1, , , , n r r n r b b − −          

br2 br 取 51= :610 52= 01: 0 0 0 则 51 52.5n, 为方程组有n-r个解： 上页 这回

11 1 1 1 , 0 0 r b b            =             12 2 2 0 , 1 0 r b b            =             1, , , . 0 0 1 n r r n r n r b b  − − −           =             取 1 2 为方程组有n-r个解: n r    则 −

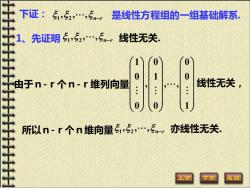
下证：51,52，5m,是线性方程组的一组基础解系 1、先证明5,52，.，5m,线性无关 由于n-r个n-r维列向量 线性无关 所以n-r个n维向量51,52，.，5n, 亦线性无关

1、先证明 1 2 , , , n r    − 线性无关. 由于ｎ-ｒ个ｎ-ｒ维列向量 1 0 0 0 1 0 , , , 0 0 1                                     线性无关， 所以ｎ-ｒ个ｎ维向量 1 2 , , , n r    − 亦线性无关. 下证： 1 2 , , , n r    − 是线性方程组的一组基础解系

2 证明解空间的任一解都可由51,5，5-，线性表示。 x=5=(.,1.)'为某一解向量， 工再构造5,52，.，5m,的一个线性组合： 7=+151+,+252+.+n5m 由，5m,是Ax的解，故也是 A的解 下面证明：7=专 上页 区回

2、证明解空间的任一解都可由 1 2 , , , n r    − 线性表示. 设 x      ( 1 1 r r n + )  = = 为某一解向量，        = + + + r r n n r + + − 1 1 2 2 再构造 1 2 , , , n r    − 的一个线性组合： n r , , , 由于  1  2   − 是 Ax 的解，故 = 0 η也是 Ax 的解 = 0 . 下面证明：   =