《线性代数》课程教学资源（PPT讲稿，C）2-1矩阵的初等变换

2.1 消元法与矩阵的初等变换 上页

2.1 消元法与矩阵的初等变换

一、消元法解线性方程组 分析：用消元法解下列方程组的过程. 引例求解线性方程组 2x1-x2-x3+x4=2, 1+X2-2X3+x4=4, 012 4x1-6x2+2x3-2x4=4,③÷2 (1) 3x1+6x2-9x3+7x4=9,④ 上页 这回

引例 (1) 一、消元法解线性方程组 求解线性方程组        + − + = − + − = + − + = − − + = 3 6 9 7 9, 4 6 2 2 4, 2 4, 2 2, 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x x x x x 1 3 4 2 分析：用消元法解下列方程组的过程．  2

解 x+22x3十4=4， 2x1-x2-3+x4=2, (1) ①K分② (B) ③÷2 2x1-3x2+x3-x4=2, 3x1+6x2-9x3+7x4=9, ④。 8+x2-2x3+x4=4, ① ②-③ ③-2① 2x2—263+2=0,- (B2) ④-3① 5x2+5x3-3x4=-6, 3 3x2-3x3+4x4=-3, 页

解 ( ) (1) B1 ( ) B2   2 1 3 2        + − + = − + − = − − + = + − + = 3 6 9 7 9, 2 3 2, 2 2, 2 4, 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x x x x x 1 3 4 2 − 2 1 2 − 3 3 4 − 3 1        − + = − − + − = − − + = + − + = 3 3 4 3, 5 5 3 6, 2 2 2 0, 2 4, 2 3 4 2 3 4 2 3 4 1 2 3 4 x x x x x x x x x x x x x 1 3 4 2

1 x1+X2-2x3+4=4, ① ②× 2 83-x3+x4=0, ③+52 (B3) 2x4=-6, ④-3② x4=-3, x1+x2-2x3+x4=4, ① ③←→④ 2x3+x4=0, ② (B) ④-2③ 8=-3. 0=0, ④ 用“回代”的方法求出解： 回

( ) B3 ( ) B4        = − = − − + = + − + = 3, 2 6, 0, 2 4, 4 4 2 3 4 1 2 3 4 x x x x x x x x x 1 3 4 2 + 5 2 2 1  3 4 − 3 2 2        = = − − + = + − + = 0 0, 3, 0, 2 4, 4 2 3 4 1 2 3 4 x x x x x x x x 1 3 4 3  2 4 − 2 4 3 用“回代”的方法求出解：

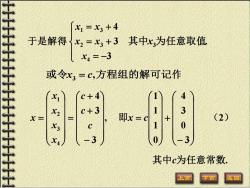
x1=X3+4 于是解得x2=x3+3其中x为任意取值 X4=-3 或令x3=c,方程组的解可记作 c+4 c+3 x= 即x=c (2) -3 其中c为任意常数

于是解得      = − = + = + 3 3 4 4 2 3 1 3 x x x x x . 其中x3为任意取值 或令x3 = c,方程组的解可记作 , 3 3 4 4 3 2 1               − + + =               = c c c x x x x x 其中c为任意常数.               − +               = 3 0 3 4 0 1 1 1 即x c （2）

小结： 1.上述解方程组的方法称为消元法， 2.始终把方程组看作一个整体变形，用到如 下三种变换 (1)交换方程次序： (①与①相互替换) (2)以不等于0的数乘某个方程； (以①×k替换①) (3)一个方程加上另一个方程的倍 (以①+k⑦替换⑦) 区回

小结： 1．上述解方程组的方法称为消元法． 2．始终把方程组看作一个整体变形，用到如 下三种变换 （1）交换方程次序； （2）以不等于０的数乘某个方程； （3）一个方程加上另一个方程的k倍． （ i 与 j 相互替换） （以 i  k 替换 i ） （以 i + k j 替换 i ）

3.上述三种变换都是可逆的. 若A00(B,则(B02(4: 若(A)①xk(B),则(B)D÷k(A) 若(0+D(B,则(B)-(A. 由于三种变换都是可逆的，所以变换前的 方程组与变换后的方程组是同解的.故这三种 变换是同解变换

3．上述三种变换都是可逆的． 由于三种变换都是可逆的，所以变换前的 方程组与变换后的方程组是同解的．故这三种 变换是同解变换． i j 若(A) (B),  则(B) (A); i  j + k 若(A) (B), i j 若(A) (B), i  k 则(B) (A); i  k 则(B) (A). i − k j

二、矩阵的定义 由m×n个数g(i=1,2,m;j=-1,2,n) 排成的m行n列的数表 11 012 L21 22 Aml Am2 称为m×n矩阵.简称m×n矩阵. 记作 区回

二、矩阵的定义 由 个数 排成的 行 列的数表 m n m n a (i m j n) ij = 1,2,  , ; = 1,2,  , m m mn n n a a a a a a a a a       1 2 21 22 2 11 12 1 称为 mn 矩阵.简称 m  n 矩阵. 记作

主对角线 l12 元素 32 4- 行标 列标 副对角线 简记为A=Axn-(a)=(ag 元素是实数的矩阵称为实矩阵 元素是复数的矩阵称为复矩阵 上页

              = m m mn n n a a a a a a a a a A        1 1 21 22 2 11 12 1 简记为 ( ) ( ). ij m n A = Am n = aij = a   元素是实数的矩阵称为实矩阵, 元素是复数的矩阵称为复矩阵. 主对角线 副对角线 元素 行标 列标

例如 03 647 是一个2×4实矩阵， 136 21 2 2 是一个3×3复矩阵， 22 2) 124 是一个3×1矩阵 (2359) (4) 是一个1×4矩阵， 是一个1×1矩阵 上页 区回

例如       − 9 6 4 3 1 0 3 5 是一个 24 实矩阵,           2 2 2 2 2 2 13 6 2i 是一个 33 复矩阵,           4 2 1 是一个 31 矩阵, (2 3 5 9) 是一个 14 矩阵, (4) 是一个 11 矩阵