《线性代数》课程教学课件(讲稿,B)第三章 矩阵的运算 §3.1矩阵的运算

第三章矩阵的运算 §3.1矩阵的运算 §3.2逆矩阵 §3.3初等矩阵 §3.4分块矩阵
第三章矩阵的运算 §3.1矩阵的运算 §3.2逆矩阵 §3.3初等矩阵 §3.4分块矩阵

§3.1矩阵的运算 一、矩阵加法 二、矩阵的数乘 三、矩阵乘法 四、矩阵转置 五、n阶矩阵的行列式 六、共轭矩阵
§3.1 矩阵的运算 一、矩阵加法 二、矩阵的数乘 三、矩阵乘法 四、矩阵转置 五、n阶矩阵的行列式 六、共轭矩阵

第一节矩阵运算 一、两个概念 1.同型矩阵:行数与列数分别相等的矩阵称为同型 矩阵. 2.矩阵相等: A=(ag)mxn,B=(b;)mxn,且ay=b,→A=B (i=1,.,m;j=1,.,n) 注意:矩阵相等与矩阵等价的区别
1.同型矩阵:行数与列数分别相等的矩阵称为同型 矩阵. 2.矩阵相等: ( ) , ( ) , ( 1, , ; 1, , ) A a B b a b A B ij m n ij m n ij ij i m j n 且 一、两个概念 注意:矩阵相等与矩阵等价的区别. 第一节 矩阵运算

3.特殊矩阵: 零矩阵:元素全是零的矩阵称为零矩阵记作:O. 设矩阵A=(a)mxn’称矩阵-(a)mxn为A的负矩阵, 记作-A,即-A=-(a)mxn 二、矩阵加法 定义3.1.1设矩阵A=(a,)mxn,B=(b)mx’ 称矩阵 C=(aj+bij)mxn 为矩阵A与矩阵B的和,记作C=A+B. 注意:两个矩阵必须是同型矩阵才可以相加
二、矩阵加法 ( ) , ( ) ( ) 3.1.1 . ij m n ij m n ij ij m n A a B b C a b A B C A B 设矩阵 ,称矩阵 和 为矩阵 与矩阵 的 ,记作 定义 零矩阵:元素全是零的矩阵称为零矩阵.记作: O. ( ) ( ) ( ) . ij m n ij m n ij m n A a a A A A a 设矩阵 ,称矩阵 为 的 , 记作 ,即 负矩阵 注意:两个矩阵必须是同型矩阵才可以相加. 3.特殊矩阵:

矩阵加法的性质: A,B,C,O均为m×n矩阵 1.A+B=B+A 2.(A+B)+C=A+(B+C) 3.A+0=0+A=A 4.A+(-A)=(-A)+A=O 5.矩阵减法可定义为 A-B=A+(-B)=(aij-bij)nxn
矩阵加法的性质: A,B,C,O均为mn矩阵 1. A B B A 2. (A B) C A (B C) 3. AO O A A 4. A(A) (A) A O 5. ( ) ( ) A B A B a b ij ij m n 矩阵 可定义为 减法
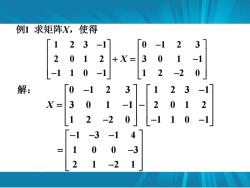
例1求矩阵X,使得 123-1 0 -1 23 20 1 2+X= 3 0 1 -1 -11 0 -1 1 2 -2 0 解: 0 -1 2 3 2 -1 X= 3 0 1 -1 - 2 0 2 1 0 -110-1 -1 4 S 1 0 -3 2 1 -2 1
1 1 2 3 1 0 1 2 3 2 0 1 2 3 0 1 1 1 1 0 1 1 2 2 0 X X 例 求矩阵 ,使得 解: 0 1 2 3 1 2 3 1 3 0 1 1 2 0 1 2 1 2 2 0 1 1 0 1 X 1 3 1 4 1 0 0 3 2 1 2 1

三、数与矩阵的乘法 定义3.1.2设矩阵A=(a)n,九是一个数,矩阵 (2a,)xn称为数与矩阵的乘积,记作九A或A几, 即 2A=A九=(2Lj)mxn 注:数乘矩阵与数乘行列式是显然是不同的. (1)数称行列式是数乘到行列式的其中一行或列上 (2)数乘矩阵是数乘到矩阵的每一行的每一个元素上
三、数与矩阵的乘法 ( ) , , ( ) ( ) 3.1.2 ij m n ij m n ij m n A a a A A A A a A 数 设矩阵 是一个数 矩阵 称为 记作 或 , 即 与矩阵 , 定 的乘积 义 注:数乘矩阵与数乘行列式是显然是不同的. (1)数称行列式是数乘到行列式的其中一行或列上. (2)数乘矩阵是数乘到矩阵的每一行的每一个元素上

数乘的性质: 设A,B是m×矩阵,2,是数, 1.几(uA)=(几)A 2.(兄+)A=兄A+uA 3.几(A+B)=几A+2B 4.1A=A 5.0A=0 6.(-1)A=-A
数乘的性质: 2. ( ) A A A 设A B m n , 是 矩阵, , 是数, 3. ( ) A B A B 1. ( ) ( ) A A 4. 1A A 5. 0A O 6. ( 1) A A

例2设A= :28= 「-3 C 解: 1 4-1-10+1+2-2-0+1 2A-B+-C= 3 2+2+44-3-2-4-1+3 23-1 8-1-2
2 0 1 1 1 0 2 , , 1 2 2 2 3 1 3 6 3 1 2 . 12 6 9 3 A B C A B C 例 设 ,求 1 4 1 1 0 1 2 2 0 1 2 3 2 2 4 4 3 2 4 1 3 A B C 2 3 1 8 1 2 解:

四、矩阵的乘法 1.定义 定义3.1.3设A=(a)是一个m×s矩阵,B=(b,) 是一个s×n矩阵,作m×n矩阵C=(c),其中 Cy anby anba++agby =anbyr k=1 矩阵C称为矩阵A与矩阵B的乘积, 记作C=AB,即
1 1 2 2 1 ( ) , ( ) , ( ) 3.1.3 , ij ij ij s ij i j i j is sj ik kj k A a m s B b s n m n C c c a b a b a b a b C A B C AB 设 是一个 矩阵 是一个 矩阵 作 矩阵 ,其中 , 矩阵 称为矩阵 与矩阵 的 , 记作 乘积 定义 即 1.定义 四、矩阵的乘法
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《线性代数》课程教学课件(讲稿,B)§3.2 逆矩阵.pdf
- 《线性代数》课程教学课件(讲稿,B)§3.3 初等矩阵.pdf
- 《线性代数》课程教学课件(讲稿,B)§3.4 分块矩阵.pdf
- 《线性代数》课程教学课件(讲稿,B)第二章 矩阵与向量 §2.1消元法与矩阵的初等变换.pdf
- 《线性代数》课程教学课件(讲稿,B)向量及其线性运算.pdf
- 《线性代数》课程教学课件(讲稿,B)向量组的线性相关性.pdf
- 《线性代数》课程教学课件(讲稿,B)矩阵的秩.pdf
- 《线性代数》课程教学课件(讲稿,B)第一章 第一节.pdf
- 《线性代数》课程教学课件(讲稿,B)行列式的性质与计算.pdf
- 《线性代数》课程教学课件(讲稿,B)第一章 行列式 §1.4 克拉默法则.pdf
- 《线性代数》课程教学课件(PPT讲稿,B)行列式的概念.ppt
- 《线性代数》课程教学课件(PPT讲稿,B)行列式的性质与计算.ppt
- 《线性代数》课程教学课件(PPT讲稿,B)克拉默法则.ppt
- 《线性代数》课程教学课件(讲稿,B)第一章 行列式的定义.pdf
- 《线性代数》课程教学课件(讲稿,B)行列式的性质.pdf
- 《线性代数》课程教学课件(讲稿,B)n阶行列式的计算.pdf
- 《线性代数》课程教学课件(讲稿,B)克拉默法则.pdf
- 《高等数学》课程教学资源(PPT课件)第七章微分方程_第七章目录.ppt
- 《高等数学》课程教学资源(PPT课件)第七章微分方程_第一节微分方程的基本概念.ppt
- 《高等数学》课程教学资源(PPT课件)第七章微分方程_第二节可分离变量的微分方程.ppt
- 《线性代数》课程教学课件(讲稿,B)§4.3 非齐次线性方程组.pdf
- 《线性代数》课程教学课件(讲稿,B)§4.2 齐次线性方程组.pdf
- 《线性代数》课程教学课件(讲稿,B)第四章 线性方程组 §4.1 线性方程组的解的判别.pdf
- 《线性代数》课程教学资源(PPT讲稿,C)5-4实对称矩阵的相似对角形.ppt
- 《线性代数》课程教学资源(PPT讲稿,C)5-3相似矩阵.ppt
- 《线性代数》课程教学资源(PPT讲稿,C)5-2方阵的特征值与特征向量.ppt
- 《线性代数》课程教学资源(PPT讲稿,C)5-1向量的内积.ppt
- 《线性代数》课程教学资源(PPT讲稿,C)4-3非齐次线性方程组.ppt
- 《线性代数》课程教学资源(PPT讲稿,C)4-2齐次线性方程组.ppt
- 《线性代数》课程教学资源(PPT讲稿,C)4-1线性方程组.ppt
- 《线性代数》课程教学资源(PPT讲稿,C)3-5习题课.ppt
- 《线性代数》课程教学资源(PPT讲稿,C)3-4分块矩阵.ppt
- 《线性代数》课程教学资源(PPT讲稿,C)3-3初等矩阵.ppt
- 《线性代数》课程教学资源(PPT讲稿,C)3-2逆矩阵.ppt
- 《线性代数》课程教学资源(PPT讲稿,C)3-1矩阵的运算.ppt
- 《线性代数》课程教学资源(PPT讲稿,C)2-4矩阵的秩.ppt
- 《线性代数》课程教学资源(PPT讲稿,C)2-3向量组的线性相关性.ppt
- 《线性代数》课程教学资源(PPT讲稿,C)2-2向量及其线性运算.ppt
- 《线性代数》课程教学资源(PPT讲稿,C)2-1矩阵的初等变换.ppt
- 《线性代数》课程教学资源(PPT讲稿,C)1-5习题课.ppt
