《高等数学》课程教学资源（PPT课件）第七章微分方程_第二节可分离变量的微分方程

第二节可分离变量的微分方程 一、概念及解法 二、举例 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 可分离变量的微分方程 一、概念及解法 二、举例

第二节可分离变量的微分方程 概念及解法 1.定义 在本节讨论如下形式的一阶微分方程 出W→Ox-xn 定义在一阶微分方程 张功中，若函数化川 可分离变量，即f化，)=p(c)y),则称该一阶微分 为可分离变量的微分方程 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 可分离变量的微分方程 一、概念及解法 在本节讨论如下形式的一阶微分方程 ( , ) , d d f x y x y = 定义 在一阶微分方程 ( , ) d d f x y x y = 中，若函数f (x, y) 可分离变量，即 f (x , y) =  (x)  (y)，则称该一阶微分 为可分离变量的微分方程. 1. 定义 Q(x, y)dy = P(x, y)dx

第二节可分离变量的微分方程 2.解法 Stepl分离变量设y=fx,)是可分离变量的微 dx 分方程，即业=0(w),分离变量，得 dx 1 y=o(x)dx; w(r) Step2两边积分设y=gx)是该方程的解，则有 1 g'(x)dx≡gp(x)dx, wIg(x)] 1 两边积分 [g(x)] g'(x)dr≡∫p(x)drx, 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 可分离变量的微分方程 2. 解法 Step1 分离变量 设 ( , ) d d f x y x y = 是可分离变量的微 分方程，即 ( ) ( ) , d d x y x y =   分离变量，得 d ( )d ; ( ) 1 y x x y   = Step2 两边积分 设 y = g(x) 是该方程的解，则有 ( )d ( )d , [ ( )] 1 g x x x x g x      两边积分 ( )d ( )d , [ ( )] 1    g  x x  x x g x  

第二节可分离变量的微分方程 g(x)dr≡p(x)dr, ∫-jatr 设左右两端的原函数分别为平(y)、Φx),则有 平y)=D(x)+C(C为任意常数) 上式即为方程的通解，称之为隐式通解 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 可分离变量的微分方程 ( )d ( )d , [ ( )] 1    g  x x  x x g x   d ( )d . ( ) 1   y = x x y   设左右两端的原函数分别为  (y)、 (x)，则有  (y) = (x) + C (C 为任意常数). 上式即为方程的通解，称之为隐式通解

第二节可分离变量的微分方程 二、举例 例1求微分方程张-2w的通解 解 例2解初值问题 xdx+(x2+1)dy=0, ylk-0=1. 解 例3求微分方程 =sin2(x-y+)的通解。 dx 解立 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 可分离变量的微分方程 二、举例 例1 求微分方程 xy x y 2 d d = 的通解. 第二节 可分离变量的微分方程 解 例1 求微分方程 xy x y 2 d d = 的通解. 分离变量，得 2 d , d x x y y = 两边积分，得 2 d , d   = x x y y 所以通解为 ln | | , 1 2 y = x +C 1 2 e x C y + =  e , 2 x = C e . 2 x y = C 积分曲线如图所示. x y O 2 e x y = C 例2 解初值问题第二节 可分离变量的微分方程 解 分离变量，得 d , 1 d 1 2 x x x y y + = − 两边积分，得 d , 1 d 1   2 + = − x x x y y 所以通解为 1 . 2 y x + = C 积分曲线如图所示. 例2 解初值问题    = + + = = | 1. d ( 1)d 0 , 0 2 x y x y x x y ln( 1) , 2 1 ln 1 2 y = − x + +C 由初始条件可得 C = 1，故特解 为 1 1. 2 y x + = x y O    = + + = = | 1. d ( 1)d 0 , 0 2 x y x y x x y 例3 求微分方程 sin ( 1) d d 2 = x − y + x y 的通解. 第二节 可分离变量的微分方程 解 令 u = x – y + 1， 例3 求微分方程 sin ( 1) d d 2 = x − y + x y 的通解. 则 u = 1 – y , 原方程变为 1 – u = sin2 u， 即 cos . d d 2 u x u = 化为可分离变量的微分方程， tan u = x +C . tan(x − y +1) = x + C ( C 为任意常数 ). 所求通解为 解之得 x y O

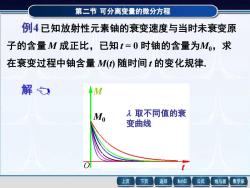
第二节可分离变量的微分方程 例4已知放射性元素铀的衰变速度与当时未衰变原 子的含量M成正比，已知t=0时铀的含量为Mo,求 在衰变过程中铀含量M)随时间t的变化规律 解 M 2取不同值的衰 变曲线 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 可分离变量的微分方程 子的含量 M 成正比，已知 t = 0 时铀的含量为M0，求 在衰变过程中铀含量 M(t) 随时间 t 的变化规律. 例4 已知放射性元素铀的衰变速度与当时未衰变原 第二节 可分离变量的微分方程 解 子的含量 M 成正比，已知 t = 0 时铀的含量为M0，求 在衰变过程中铀含量 M(t) 随时间 t 的变化规律. 例4 已知放射性元素铀的衰变速度与当时未衰变原 根据题意有 ( 0) d d = − M   t M M t=0 = M0 这是一个可分离变量的微分方程， 解之得通解为 e . t M C − = 利用初始条件, 得 , C = M0 故所求铀的变化规律为 e . 0 t M M − = t M M0  取不同值 的衰变曲线 O t M M0  取不同值的衰 变曲线 O

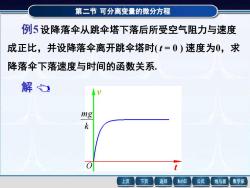
第二节可分离变量的微分方程 例5设降落伞从跳伞塔下落后所受空气阻力与速度 成正比，并设降落伞离开跳伞塔时(t=0)速度为0，求 降落伞下落速度与时间的函数关系. 解 mg k 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 可分离变量的微分方程 成正比，并设降落伞离开跳伞塔时( t = 0 ) 速度为0，求 例5 设降落伞从跳伞塔下落后所受空气阻力与速度 降落伞下落速度与时间的函数关系. 第二节 可分离变量的微分方程 解 成正比，并设降落伞离开跳伞塔时( t = 0 ) 速度为0，求 例5 设降落伞从跳伞塔下落后所受空气阻力与速度 降落伞下落速度与时间的函数关系. 根据牛顿第二定律列方程 = t v m d d mg − kv , 0 . 初始条件为 v t=0 = 分离变量，得 , d d m t mg kv v = − 两边积分，得 ln ( ) . 1 C m t mg k v k − − = + t v k mgO

第二节可分离变量的微分方程 例6有高1m的半球形容器，水从它的底部小孔流出， 小孔横截面积S=1cm2.开始时容器内盛满了水，求水 从小孔流出过程中，容器里水面的高度h随时间t的变 化规律 解 dh 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 可分离变量的微分方程 例6 有高 1m 的半球形容器, 水从它的底部小孔流出, 从小孔流出过程中, 容器里水面的高度 h 随时间 t 的变 小孔横截面积 S = 1cm2 . 开始时容器内盛满了水, 求水 化规律. 第二节 可分离变量的微分方程 解 例6 有高 1m 的半球形容器, 水从它的底部小孔流出, 从小孔流出过程中, 容器里水面的高度 h 随时间 t 的变 小孔横截面积 S = 1cm2 . 开始时容器内盛满了水, 求水 化规律. 由水力学知, 水从孔口流出的流量为 t V Q d d = = k S 2 g h 流量系数 孔口截面面积 重力加速度 1m h h r h+dh 1m h h r h+dh