《高等数学》课程教学资源（PPT课件）第七章微分方程_第六节高阶线性微分方程

第六节高阶线性微分方程 一、二阶线性微分方程举例 二、二阶线性微分方程解的结构 *三、常数变易法 上页 下页 返回 MathGS 公式 线与面 数学家

第六节 高阶线性微分方程 一、二阶线性微分方程举例 二、二阶线性微分方程解的结构 *三、常数变易法

第六节高阶线性微分方程 二阶线性微分方程举例 例1设有一个弹簧，它的上端固定，下端挂一个质 量为m的物体.当物体处于静止状态时，作用在物体上 的重力与弹性力大小相等、方向相反.这个 位置就是物体的平衡位置.建立如图所示的 的坐标系，原点O为平衡位置， 设在振动过程中，物体的位置函数为 x=x().下面来求振动规律. 上页 下页 返回 MathGS 公式 线与面 数学家

第六节 高阶线性微分方程 一、 二阶线性微分方程举例 例1 设有一个弹簧，它的上端固定，下端挂一个质 x x O 量为 m 的物体. 当物体处于静止状态时，作用在物体上 的重力与弹性力大小相等、方向相反. 这个 位置就是物体的平衡位置. 建立如图所示的 的坐标系，原点 O 为平衡位置. 设在振动过程中，物体的位置函数为 x = x(t) . 下面来求振动规律

第六节高阶线性微分方程 ()自由振动情况物体所受的力有： 弹性恢复力f=-cx (虎克定律) dx 阻力 R=- “dt 据牛顿第二定律得 d2x dx m =-Cx- 'dt 令 2n=,k2=C m m 则得有阻尼自由振动方程： d'x dx di2 +2 +k2x=0 dt 上页 下页 返回 MathGS 公式 线与面 数学家

第六节 高阶线性微分方程 x x O (1) 自由振动情况 弹性恢复力 物体所受的力有: (虎克定律) 据牛顿第二定律得 , 2 m c 2 , k = m n  = 则得有阻尼自由振动方程: 0 . d d 2 d d 2 2 2 + + k x = t x n t x 阻力 令

第六节高阶线性微分方程 (2)强迫振动情况若物体在运动过程中还受铅直外力 F=Hs如pr作用，令h=仁，则得强迫振动方程： m 2kxhsm pl 上页 下页 返回 MathGS 公式 线与面 数学家

第六节 高阶线性微分方程 (2) 强迫振动情况 若物体在运动过程中还受铅直外力 ， m H h = 则得强迫振动方程: sin . d d 2 d d 2 2 2 k x h pt t x n t x + + = F = H sin pt 作用，令

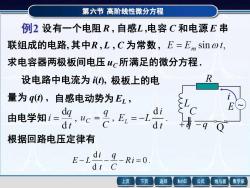
第六节高阶线性微分方程 例2设有一个电阻R,自感L,电容C和电源E串 联组成的电路，其中R,L,C为常数，E=E sin @t, 求电容器两极板间电压uc所满足的微分方程. 设电路中电流为①)，极板上的电 量为q(④，自感电动势为EL, 由电学知1=9c-名，E=- di 根据回路电压定律有 E-L di -Ri=0 dt C 上页 下页 返回 MathGS 公式 线与面 数学家

第六节 高阶线性微分方程 求电容器两极板间电压 uC 所满足的微分方程 . 0 . d d − − − Ri = C q t i E L 例2 联组成的电路, 其中R , L , C 为常数 , 设电路中电流为 i(t), 量为 q(t) , 自感电动势为 EL , 由电学知 根据回路电压定律有 设有一个电阻 R , 自感L ,电容 C 和电源 E 串 极板上的电 + q ‖ L E ~ R Q C − q i

第六节高阶线性微分方程 化为关于.的方程，i=Cd, 故有 LCCduc e=t d t2 dt 令B= R 1 1 ,00= LC 串联电路的振荡方程： duc+uc= sin ot. dt2 LC 如果电容器充电后撤去电源(E=0),则得 duc+2 dt2 duc+o4。=0 上页 下页 返回 MathGS 公式 线与面 数学家

第六节 高阶线性微分方程 , 1 , 2 0 L LC R  =  = sin . d d 2 d d 2 2 0 2 t LC E u t u t u m C C C +  + =  串联电路的振荡方程: 2 2 d d t u LC C t u RC C d d + + uC E sin t . = m  化为关于 uc 的方程, 故有 如果电容器充电后撤去电源 ( E = 0 ) , 则得 0 . d d 2 d d 2 2 0 2 + + c = C C u t u t u   令

第六节高阶线性微分方程 例1和例2虽然是两个不同的实际问题，但在求解时 都要解一个形式相同的微分方程： 要+m张ar=a 上述方程称为二阶线性微分方程.当fx)≡0时，叫 做齐次的；否则叫做非齐次的. n阶线性微分方程的形式是： y()+a(x)y-+.+a(x)y'+a,(x)y=f(x). 上页 下页 返回 MathGS 公式 线与面 数学家

第六节 高阶线性微分方程 例1和例2虽然是两个不同的实际问题，但在求解时 都要解一个形式相同的微分方程： ( ) ( ). d d ( ) d d 2 2 Q x y f x x y P x x y + + = 上述方程称为二阶线性微分方程. 当 f (x)  0 时，叫 做齐次的；否则叫做非齐次的. n 阶线性微分方程的形式是： ( ) ( ) ( ) ( ). 1 ( 1) 1 ( ) y a x y a x y a x y f x n n n n + + + −  + = − 

第六节高阶线性微分方程 二、线性微分方程解的结构 1.齐次线性微分方程解的结构 定理1如果函数y心)与y2)是二阶齐次线性方程 y"+P(x)y'+Q(x)y=O 的两个解，那么 y=Cy(x)+C22(x)(C1,C2是任意常数) 也是该方程的解。 证明之 上页 下页 返回 MathGS 公式 线与面 数学家

第六节 高阶线性微分方程 二、 线性微分方程解的结构 1. 齐次线性微分方程解的结构 定理1 如果函数 y1 (x) 与 y2 (x) 是二阶齐次线性方程 y + P(x)y +Q(x)y = 0 的两个解，那么 ( ) ( ) 1 1 2 2 y =C y x +C y x (C1 , C2 是任意常数) 也是该方程的解. 第六节 高阶线性微分方程 证明 定理1 y1 (x) 与 y2 (x) 是 y  + P(x) y  + Q(x) y = 0 的解， 那么 ( ) ( ) 1 1 2 2 y = C y x +C y x (C1 , C2 是任意常数)也是解. 由已知可得 ( ) ( ) 0 , (1) y1 + P x y1  + Q x y1 = ( ) ( ) 0 , (2) y2  + P x y2  + Q x y2 = (1)  C1 + (2)  C2 ，得 ( ) ( )( ) ( )( ) 0 . C1 y1 +C2 y2  + P x C1 y1  +C2 y2  + Q x y1 + y2 = 这就说明 ( ) ( ) 1 1 2 2 y = C y x +C y x 也是方程的解. 证毕

第六节高阶线性微分方程 注意 y=Cy1(x)+C2y2(x)不一定是所给方程的通解 例如，y(x)是某二阶齐次方程的解，则 y2(x)=2h(x)也是齐次方程的解 但是Ch(x)+C2y2(x)=(C1+2C2)y1(x)并不是通解. 为解决通解的判别问题，下面引入函数的线性相关与 线性无关概念. 上页 下页 返回 MathGS 公式 线与面 数学家

第六节 高阶线性微分方程 注意 不一定是所给方程的通解. 例如, 是某二阶齐次方程的解, 也是齐次方程的解 但是 并不是通解． ( ) ( ) 1 1 2 2 y = C y x +C y x 则 为解决通解的判别问题, 下面引入函数的线性相关与 线性无关概念

第六节高阶线性微分方程 定义设1w),2),.,yn)为定义在区间I上的 n个函数，如果存在n个不全为零的常数k1,k2,.,km 使得当x∈I时有恒等式 k1y1)+k2Jy2c)+.+knyn()=0 成立，那么就称这个函数在区间I上线性相关，否则 称线性无关 例如，函数1，cos2x,sin2x在整个数轴上是线性相 关的.因为有恒等式1-cos2x-sin2x=0. 上页 下页 返回 MathGS 公式 线与面 数学家

第六节 高阶线性微分方程 定义 设 y1 (x) , y2 (x) , . , yn (x) 为定义在区间 I 上的 n 个函数，如果存在 n 个不全为零的常数 k1 , k2 , . , kn 使得当 x  I 时有恒等式 k1 y1 (x) + k2 y2 (x) + . + kn yn (x)  0 成立，那么就称这 n 个函数在区间 I 上线性相关，否则 称线性无关. 例如，函数 1 , cos2x , sin2x 在整个数轴上是线性相 关的. 因为有恒等式 1 - cos2x - sin2x  0