《线性代数》课程教学课件（讲稿，B）n阶行列式的计算

§1.3n阶行列式的计算 本节将简单介绍利用行列式按行（列)展开的定理 和行列式的性质计算行列式的方法，主要涉及的方法 有如下几种。 1.化行列式为特殊类型的行列式 2.降阶法 3.拆行拆列法 4.升阶法（加边法) 5.递推法 6.利用数学归纳法 下面分别通过相应的例子来阐述上述几种方法

§1.3 n阶行列式的计算 本节将简单介绍利用行列式按行（列）展开的定理 和行列式的性质计算行列式的方法,主要涉及的方法 有如下几种。 2.降阶法 3.拆行拆列法 4.升阶法（加边法） 5.递推法 6.利用数学归纳法 下面分别通过相应的例子来阐述上述几种方法。 1.化行列式为特殊类型的行列式

1.化行列式为特殊类型的行列式 例1计算 4 3 -1 -2 -6 5 3 1 2 -1 0 3 5 2 4 解： 1 2 -1 0 1 2 -1 0 2+2 1分3 -2 -6 5 3 3-4 0 -2 3 3 D 4 1 3 -1 4-3 0 -7 3 5 2 4 0 -1 5 4

4 1 3 1 2 6 5 3 1 2 1 0 3 5 2 4     1 3 1 2 1 0 2 6 5 3 4 1 3 1 3 5 2 4 r r D        2 1 3 1 4 1 2 4 3 1 2 1 0 0 2 3 3 0 7 7 1 0 1 5 4 r r r r r r           解： 1.化行列式为特殊类型的行列式 例1 计算

2 -1 0 1 2 -1 0 2→r4 0 -1 5 4 3-72 0 -1 5 4 = 0 -7 7 -1 4-23 0 0 -28 -29 0 -2 3 3 0 0 -7 -5 /1 2 -1 0 1 2 -1 0 0 -1 5 4 "4-43 0 -1 5 4 三 0 0 -7 -5 0 0 -7 -5 0 0 -28 -29 0 0 0 =-1×(-1)×(-7)×(-9)=63

2 4 1 2 1 0 0 1 5 4 0 7 7 1 0 2 3 3 r r        3 2 4 2 7 2 1 2 1 0 0 1 5 4 0 0 28 29 0 0 7 5 r r r r          3 4 1 2 1 0 0 1 5 4 0 0 7 5 0 0 28 29 r r          4 3 4 1 2 1 0 0 1 5 4 0 0 7 5 0 0 0 9 r r                  1 ( 1) ( 7) ( 9) 63

注意：例1是利用行列式的性质2、5将行列式主对 角线下方的元素全化为零（即化为上三角行列式） 行列式的值为主对角线上元素的连乘积.由于化简过 程具有程序化，因此工程技术上，常用计算机程序 计算高阶行列式的值. 例2设多项式 1 12 3 1 2-x2 2 3 f(x)= 2 3 1 5 2 3 9-x 试求fx)的根

注意：例1是利用行列式的性质2、5将行列式主对 角线下方的元素全化为零（即化为上三角行列式） 行列式的值为主对角线上元素的连乘积.由于化简过 程具有程序化，因此工程技术上，常用计算机程序 计算高阶行列式的值. 例2 设多项式 2 2 1 1 2 3 1 2 2 3 ( ) 2 3 1 5 2 3 1 9 x f x x    试求f(x)的根

解： 1 0 0 0 c2-91 C3-2c1 1 1-x2 0 0 f(x) 4-31 2 1 -3 -1 2 1 -3 3-x2 0 0 0 1 e433 1 2 1-x1 0 0 2 1 -30 =-3(1-x2)(4-x2) 2 1 -34-x2 求得x)=0的根为x1=-1,x2=1,X3=-2,x4=2

解 : 2 1 3 1 4 1 2 2 3 2 1 0 0 0 1 1 0 0 ( ) 2 1 3 1 2 1 3 3 c c c c c c x f x x          4 3 1 2 3 2 1 0 0 0 1 1 0 0 2 1 3 0 2 1 3 4 c c x x       2 2     3(1 )(4 ) x x 求得f(x)=0的根为x1=-1，x2=1，x3=-2，x4=2

a b b b 例3计算行列式 b a b b D= b b a b b b b a 解：将第2,3，n列都加到第1列得 a+(n-1)b b b a+(n-1)b b D=a+(n-1)bb b a+(n-1)bb b

b b b a b b a b b a b b a b b b D           解：将第2,3,.，n列都加到第1列得         1 1 1 1 a n b b b b a n b a b b D a n b b a b a n b b b a          例3计算行列式

1 b b b 1 a b b =[a+(n-1)b] 1 b a . b 1 b b a 1 b b b 0 a-b 0 0 0 =[a+(n-1)b]00 a-b00 =[a+(n-1)ba-bn- 0 0 0 .a-b

  b b a b a b a b b b b b a n b          1 1 1 1   ( 1)   a b a b a b b b b a n b              0 0 0 0 0 0 0 0 0 0 0 1 ( 1)  ( 1) ( ) . 1     n a n b a b

注意：行列式的每一行的各元素之和相等时常用 此法。 例如下面的行列式 x-m X2 . Xn 1 X3. D= X X2-m. Xn =∑x-m x2-m . i= X X2 Xn-m 1 1 0 1 -m 0 -m =(∑x-m(-m) i=1 i=1 1 0 -m

x x x m x x m x x m x x D n n n           1 2 1 2 1 2 此法。 注意:行列式的每一行的各元素之和相等时常用 例如下面的行列式 m m x m n i i              1 0 1 0 1 0 0 ( ) 1 1 1 ( )( )       n n i xi m m x x m x m x x x x m n n n n i i             2 2 2 1 1 1 1 ( )

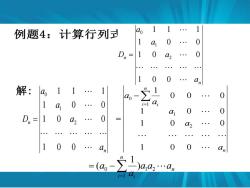
例题4：计算行列 a 1 1 1 1 a 0 0 D,= 1 0 a, . 0 1 0 0 解：la 11 .1 n 1 ao 0 0 1 41 0 . 0 i=l ai 1 a 0 0 Dn= 1 0 a, . 0 1 0 a 0 1 0 0 . an 1 0 0 an (0o -)a1a2.a i=l a

例题4：计算行列式 n n a a a a D          1 0 0 1 0 0 1 0 0 1 1 1 2 1 0  n n a a a a D          1 0 0 1 0 0 1 0 0 1 1 1 2 1 0  解: n n i i a a a a a          1 0 0 1 0 0 1 0 0 0 0 0 1 2 1 1 0    n n i i a a a a a 1 2  1 0 ) 1 (   

2、降阶法 例5计算行列式 a b c d a+b a+b+c a+b+c+d D= a 2a+b 3a+2b+c 4 4a+3b+2c+d a 3a+b 6a+3b+c 10a+6b+3c+d 解： a b C d 4-3 3-2 0 a a+b a+b+c D = 2-1 0 a 2a+b 3a+2b+c 0 a 3a+b 6a+3b+c

例5 计算行列式 2 3 2 4 3 2 3 6 3 10 6 3 a b c d a a b a b c a b c d D a a b a b c a b c d a a b a b c a b c d                    4 3 3 2 2 1 0 0 2 3 2 0 3 6 3 r r r r r r a b c d a a b a b c D a a b a b c a a b a b c              解： 2、降阶法