《高等数学》课程教学资源（PPT课件）第七章微分方程_D7习题课（2）

司题裸（二） 第十二章 二阶微分方程的 解法及立用 一、两类二阶微分方程的解法 二、微分方程的应用 HIGH EDUCATION PRESS 机动目录上页下页返回结束

二阶微分方程的 机动 目录 上页 下页 返回 结束 习题课 (二) 二、微分方程的应用 解法及应用 一、两类二阶微分方程的解法 第十二章

、i 两类二阶微分方程的解法 1.可降阶微分方程的解法一降阶法 d2y =f(x) 逐次积分求解 令p(x)= dy dx =f(x,p) dx 令p0) dy p=f0y,p〉 HIGH EDUCATION PRESS 下页返回结束

一、两类二阶微分方程的解法 1. 可降阶微分方程的解法 — 降阶法 ( ) d d 2 2 f x x y • = ) d d ( , d d 2 2 x y f x x y • = 令 x y p x d d ( ) = ( , ) d d f x p x p = ) d d ( , d d 2 2 x y f y x y • = 令 x y p y d d ( ) = 逐次积分求解 机动 目录 上页 下页 返回 结束

2.二阶线性微分方程的解法 齐次 ·常系数情形 代数法 非齐次 欧拉方程 x2y"+pxy'+qy=f(x)〉 令x=e,D=d dt [D(D-1)+pD+g.y =f(e') 练习题： P327题2； 3(6),(7)； 4(2)；8 HIGH EDUCATION PRESS 机动目录上页下页返回结束

2. 二阶线性微分方程的解法 • 常系数情形 齐次 非齐次 代数法 • 欧拉方程 x y  2 + pxy  + qy = f (x) t x e D t d d 令 = , = D(D −1) + pD + q y ( ) t = f e 练习题: P327 题 2 ; 3 (6) , (7) ; 4(2)； 8 机动 目录 上页 下页 返回 结束

解答提示 P327题2求以y=C1ex+C2e2x为通解的微分方程 提示：由通解式可知特征方程的根为1=1，乃=2， 故特征方程为(？-1)(r-2)=0,即r2-3r+2=0 因此微分方程为y”-3y'+2y=0 P327题3求下列微分方程的通解 (6)yy-y2-1=0,(7)y+2y+5y=sin2x 提示：(6)令y'=p(y),则方程变为 -p2-1=0,即 yp dy pdp dy 1+p HIGH EDUCATION PRESS 机动目录上页下页返回结束

解答提示 P327 题2 求以 为通解的微分方程 . 提示: 由通解式可知特征方程的根为 故特征方程为 因此微分方程为 P327 题3 求下列微分方程的通解 (6) 1 0, 2 yy  − y  − = (7) y  + 2y  + 5y = sin 2x . 提示: (6) 令 则方程变为 1 0 , d d 2 − p − = y p y p 机动 目录 上页 下页 返回 结束

(7)y"+2y'+5y sin2x 特征根：1,2=-1±2i, 齐次方程通解：Y=ex(C1cos2x+C2sin2x) 令非齐次方程特解为y*=Acos2x+Bsin2 代入方程可得A=么，B= 原方程通解为y=ex(C1cos2x+C2sin2x) 17cos2x-1sin 2x 思考 若(7中非齐次项改为sinx,特解设法有何变化？ 提示：sin2x=1cos2y 2 ,y*=Acos 2x+Bsin2x+D HIGH EDUCATION PRESS 机动目录上页下页返回结束

特征根: (7) y  + 2y  + 5y = sin 2x 齐次方程通解: ( cos 2 sin 2 ) 1 2 Y e C x C x x = + − 令非齐次方程特解为 代入方程可得 17 4 17 1 , A = B = − 思 考 若 (7) 中非齐次项改为 提示: 故 y* = Acos 2x + Bsin 2x + D 原方程通解为 ( cos 2 sin 2 ) 1 2 y e C x C x x = + − 特解设法有何变化 ? 机动 目录 上页 下页 返回 结束

-ay'2=0 P327题4(2) 求解 x=0=0, 2x=0=-1 提示：令y'=p(x),则方程变为 =ap dx 积分得 -1=ax+C,利用Px0=y=0=-1得C=1 再解 dy dx ,并利用x=0=0,定常数C2 1+ax y-y3=0 思考 若问题改为求解 yx=0=0,yx=0=1 则求解过程中得p2= 1-x 问开方时正负号如何确定？ HIGH EDUCATION PRESS 机动目录上页下页返回结束

P327 题4(2) 求解    0 2 y  − ay  = 0 , y x=0 = y  x=0 = −1 提示: 令 则方程变为 积分得 , 1 C1 ax p − = + 利用 1 p x=0=y  x=0 = − 得 C1 =1 再解 , 1 1 d d x ax y + − = 并利用 0 , y x=0 = 定常数 . C2 思考 若问题改为求解    0 , y x=0 = 则求解过程中得 问开方时正负号如何确定? 机动 目录 上页 下页 返回 结束

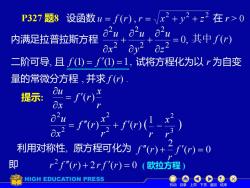
P327题8设函数1=f(r),r=x2+y2+z2在r>0 内满足拉普拉斯方程 +0+。2=0,其中f(ry 二阶可导，且f()=f')=1,试将方程化为以r为自变 量的常微分方程，并求f(r 提示： j5+o- u 0x2 利用对称性，原方程可化为f"(r)+二f'(r)=0 即 r2f"(r)+2rf"(r)=0(欧拉方程) HIGH EDUCATION PRESS 机动目录上页下页返回结束

P327 题8 设函数 在 r > 0 内满足拉普拉斯方程 0, 2 2 2 2 2 2 =   +   +   z u y u x u 二阶可导, 且 试将方程化为以 r 为自变 量的常微分方程 , 并求 f (r) . 提示: r x f r x u = ( )   =  +   2 2 2 2 ( ) r x f r x u f (r) ( ) r 1 3 2 r x − 利用对称性, 即 ( 欧拉方程 ) 原方程可化为 机动 目录 上页 下页 返回 结束

解初值问题 r2f"(r)+2rf")=0 Lf①=f')=1 令t=lnr,记D=d 则原方程化为 [DD-1)+2D]f=0即[D2+D]f=0 通解fv)=C+C2e=C+C2, 利用初始条件得特解： /r)=2-1 HIGH EDUCATION PRESS 机动目录上页下页返回结束

解初值问题: 则原方程化为 通解: 利用初始条件得特解: 机动 目录 上页 下页 返回 结束

例1.求微分方程 y”+y=x,X≤ 满足条件 y”+4y=0,x> x=0=0,yx=0=0,在x=乏处连续旦可微的解 提示：当x≤牙时，解满足 y”+y=x Vx=0=0,yx=0=0 特征根：1,2=±， 设特解：y*=Ax+B,代入方程定A,B,得y*=x 故通解为y=C1cosx+C2sinx+x 利用x=0=0,y1x-0=0,得 y=-sinx+x(x≤号) HIGH EDUCATION PRESS 机动目录上页下页返回结束

y = C cos x +C sin x + x 1 2 特征根 : , 1,2 r = i 例1. 求微分方程    2 ,  y  + y = x x  提示: 故通解为 2 4 0 ,  y  + y = x  满足条件 解满足 y  + y = x 0 , y x=0 = y  x=0 = 0 处连续且可微的解. 设特解 : y = Ax + B,  代入方程定 A, B, 得 0, 0, 利用y x=0 = y  x=0 = 得 机动 目录 上页 下页 返回 结束

由x=牙处的衔接条件可知，当x>时，解满足 y"+4y=0 lyx=-1+，yx=1 其通解：y=C1sin2x+C2cos2x 定解问题的解y=-sn2x+(1-)cos2x,x≥3 故所求解为 -sinx+x, x< y -sin2x+(1-3)cos2x,x≥经 HIGH EDUCATION PRESS 机动目录 下页返回结束

处的衔接条件可知, y  + 4y = 0 解满足 故所求解为 y = 2 2 2 1 sin 2 (1 )cos 2 ,   − x + − x x  y C sin 2x C cos 2x 其通解 = 1 + 2 : 定解问题的解: 2 2 2 1 sin 2 (1 )cos 2 ,   y = − x + − x x  机动 目录 上页 下页 返回 结束