《高等数学》课程教学资源（PPT课件）第七章微分方程_第五节可降阶的高阶微分方程

第五节可降阶的高阶微分方程 一、y四=fx)型 二、y=fx,y)型 三、y”=f0,y)型 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 可降阶的高阶微分方程 一、y (n) = f (x) 型 二、y  = f (x , y  ) 型 三、y  = f (y , y  ) 型

第五节可降阶的高阶微分方程 一、y网=fx)型 形如ym=f(x)的高阶微分方程的求解方法： 方程两边接连积分n次，即可得到含有n个任意常 数的通解 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 可降阶的高阶微分方程 一、 y (n) = f (x) 型 形如 y (n) = f (x) 的高阶微分方程的求解方法： 方程两边接连积分 n 次，即可得到含有 n 个任意常 数的通解

第五节可降阶的高阶微分方程 例1解方程y"=e2x-cosx. 解 例2质量为m的质点受力F的作用沿Ox轴作直线 运动，设力F仅是时间t的函数：F=F().在开始时刻 t=0时FO)=F,随着时间的增大，此力F均匀地减 小，直到t=T时F(T=0.如果开始时质点在原点，且 初速度为0，求质点的运动规律 解之 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 可降阶的高阶微分方程 例1 解方程 第五节 可降阶的高阶微分方程 解 例1 解方程 e cos . 2 y x x  = − 对所给方程接连积分三次，得 e sin , 2 1 2 y x C x  = − + e cos , 4 1 2 2 y x Cx C x  = + + + . 2 e sin 8 1 2 3 1 2 1 2       = + + + + = C y x C x C x C C x 例2 质量为 m 的质点受力F 的作用沿Ox 轴作直线 运动，设力 F 仅是时间 t 的函数: F = F(t). 在开始时刻 t = 0 时 F(0) = F0，随着时间的增大，此力 F 均匀地减 小，直到 t = T 时 F(T) = 0. 如果开始时质点在原点，且 初速度为0，求质点的运动规律. 第五节 可降阶的高阶微分方程 解 例2 质量为 m 的质点受力F 的作用沿 Ox 轴作直线 运动，设力 F 仅是时间 t 的函数: F = F(t). 在开始时刻 t = 0 时 F(0) = F0，随着时间的增大，此力 F 均匀地减 小，直到 t = T 时 F(T) = 0. 如果开始时质点在原点， 且 初速度为0，求质点的运动规律. 设运动规律为 x = x(t) . O x y F0 T       = − T t F(t) F0 1 根据牛顿第二定律，可得初值问题

第五节可降阶的高阶微分方程 二、y”=f心，Jy)型 形如y”=fc,y)的高阶微分方程的求解方法： 令y'=p,则y”=p',原方程变形为 p'=f(x,p). 这是一个以x为自变量，以p为函数的一阶微分方程， 解出p后，在方程y=两边再积一次分即可得原方程 的通解。 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 可降阶的高阶微分方程 二、y = f (x , y) 型 形如 y = f (x , y  ) 的高阶微分方程的求解方法： 令 y = p， 则 y = p ，原方程变形为 p = f (x , p ). 这是一个以 x 为自变量，以 p 为函数的一阶微分方程， 解出 p 后，在方程y = p两边再积一次分即可得原方程 的通解

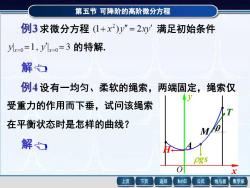
第五节可降阶的高阶微分方程 例3求微分方程(1+x2)y”=2y满足初始条件 儿0=1，y儿x0=3的特解 解 例4设有一均匀、柔软的绳索，两端固定，绳索仅 受重力的作用而下垂，试问该绳索 在平衡状态时是怎样的曲线？ M 解 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 可降阶的高阶微分方程 x y O A M H gs T  例3 求微分方程 满足初始条件 的特解. 第五节 可降阶的高阶微分方程 解 例3 求微分方程 (1+ x ) y  = 2xy  2 满足初始条件 y| x=0 =1, y | x=0 = 3 的特解. 令 y = p，则 y = p ，原方程变形为 (1 ) 2 , 2 + x p  = xp , 1 2 d d 2 p x x x p + = 分离变量，得 d , 1 d 2 2 x x x p p + = 两边积分，得 ln | | ln(1 ) , 2 p = + x +C (1 ) . 2 1 p = y  = C + x 上式再两边积分，得 ) . 3 1 ( 2 3 y = C1 x + x +C 由初始条件可求得特解为 3 1. 3 y = x + x + 例4 设有一均匀、柔软的绳索，两端固定，绳索仅 受重力的作用而下垂，试问该绳索 在平衡状态时是怎样的曲线？ 第五节 可降阶的高阶微分方程 解 例4 设有一均匀、柔软的绳索，两端固定，绳索仅 受重力的作用而下垂，试问该绳索 在平衡状态时是怎样的曲线？ x y O A M H gs T  取坐标系如图. 考察最低点 A 到任意点M ( x, y ) 弧段的受力情况: 弧段重力大小 gs (  : 密度, s :弧长)． A 点受水平张力 H， M 点受切向张力T

第五节可降阶的高阶微分方程 三、y”=f心，y)型 形如y”=f0y,y)的高阶微分方程的求解方法： 令y'=p,则y”-2-p.dy=p2 dx dy dx dy 故方程化为 dp=f(y.p) dy 这是一个以y为自变量，以p为函数的一阶微分方程， 解出p后，在方程y'=两边再积一次分即可得原方程 的通解 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 可降阶的高阶微分方程 三、y = f (y , y) 型 形如 y = f (y , y  ) 的高阶微分方程的求解方法： 令 y = p， 则 x p y d d  = x y y p d d d d =  故方程化为 这是一个以 y 为自变量，以 p 为函数的一阶微分方程， 解出 p 后，在方程y = p两边再积一次分即可得原方程 的通解. , d d y p = p ( , ). d d f y p y p p =

第五节可降阶的高阶微分方程 例5求解yy”-y2=0. 解 例6一个离地面很高的物体，受地球引力的作用由 静止开始落向地面，求它落到地面时的速度和所需时间 (不计空气阻力). 解 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 可降阶的高阶微分方程 例5 求解 第五节 可降阶的高阶微分方程 解 例5 求解 0 . 2 yy  − y  = 代入方程得 0, d d 2 − p = y p y p , d d y y p p = 两端积分得 ln ln ln , C1 p = y + , 1 p = C y . 1  y  = C y 故所求通解为 e . 1 2 C x y = C y  = p, , d d y p 令 则 y  = p 例6 静止开始落向地面, (不计空气阻力). 一个离地面很高的物体, 受地球引力的作用由 求它落到地面时的速度和所需时间 第五节 可降阶的高阶微分方程 解 y M : 地球质量 m : 物体质量 例6 静止开始落向地面, (不计空气阻力). 建立如图所示的坐标系. 则有 = 2 2 d d t y m , 2 y k m M − , 0 y l t= = 0 , y  t=0 = , d d t y v = t v t y d d d d 2 2 = t y y v d d d d =  . d d y v = v 代入方程得 d d , 2 y y k M v v = − 积分得 . 2 1 2 C y k M v = + 一个离地面很高的物体, 受地球引力的作用由 求它落到地面时的速度和所需时间 设 则 y