《线性代数》课程教学资源（PPT讲稿，C）3-5习题课

第二章 矩阵及其运算 习题课 主要内容 x+y= 典型例题 测验题 带助式

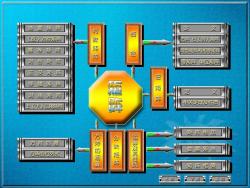
转置矩阵 定 特殊矩阵 锡 (反)对称矩阵 方阵行（列）矩阵 幂等矩阵 念 司型矩阵和相等矩阵 对 合矩 阵 矩阵单矩阵 正交矩阵 伴随矩阵 对角矩阵 逆矩阵 定 相关定埋及性质 (下)三角矩阵 矩阵相加 方阵的幂 方阵的行列式 万阵的运算 分块矩阵 运算及具性质 数乘矩阵 矩阵相采 上贝 返回

1矩阵的定义 由m×n个数a(i=1,2,.m;j=1,2,.n)排成m 行n列的数表 11 12 Qin A- 021 L22 Q2n (1) Aml am2 amn 叫做m行n列矩阵，简称m×n矩阵. 上页 下页 返回

, . (1) ( 1,2, ; 1,2, ) 1 2 2 1 2 2 2 1 1 1 2 1 叫 做 行 列矩阵 简 称 矩 阵 行 列的数表 由 个 数 排 成 m n m n a a a a a a a a a A n m n a i m j n m m m mn n n ij              =  = =          １ 矩阵的定义

其中m×n个数叫做矩阵A的元素，a:叫做矩 阵A的第行第列元素. 元素是实数的矩阵叫做实矩阵， 元素是复数的矩阵叫做复矩阵 ()式可简记为 A=(ajmxn或A=(a m×n矩阵A也记作Amxm. 上页

. . . , 元素是复数的矩阵叫做复矩阵 元素是实数的矩阵叫做实矩阵 阵 的 第 行 第 列元素 其 中 个数叫做矩阵 的元素 叫做矩 A i j m  n A aij . ( ) ( ), (1) m n A A A a A a m n ij m n ij    = = 矩 阵 也记作 或 式可简记为

2 方阵！ 列矩阵 行矩阵 对(1)式，当m=n时，A称为n阶方阵. 只有一列的矩阵A= 叫做列矩阵 am 只有一行的矩阵A=(a1a2.am)叫做 行矩阵 返回

. ( ) ; 1 2 2 1 行矩阵 只有一行的矩阵 叫 做 只有一列的矩阵 叫做列矩阵 A a a a a a a A n m   =             = ２ 方阵 列矩阵 行矩阵 对(1)式,当m = n时, A称 为n阶方阵

3 同型矩阵和相等矩阵 两个矩阵的行数相等、列数也相等时，就称 它们是同型矩阵. 如果A=(a)与B=(b)是同型矩阵并且它 们的对应元素相等即 a=bg(i=1,2,.,m;j=1,2,n). 那么就称矩阵A与矩阵B相等，记作A=B

两个矩阵的行数相等、列数也相等时，就称 它们是同型矩阵． , . ( 1,2, , ; 1,2, , ). , ( ) ( ) , A B A B a b i m j n A a B b ij ij ij ij = = = = = = 那么就称矩阵 与矩阵 相 等 记 作 们的对应元素相等即 如 果 与 是同型矩阵 并且它   ３ 同型矩阵和相等矩阵

4 零矩阵」 单位矩阵 元素都是零的矩阵称为零矩阵记作O 主对角线上的元素都是，其余元素都是零的 n阶方阵，叫做n阶单位阵简记作E

４ 零矩阵 单位矩阵 元素都是零的矩阵称为零矩阵,记作O. , , . 1, n阶方阵 叫 做n阶单位阵 简记作E 主对角线上的元素都是 其余元素都是零的

5 矩阵相加 设A=(a)mxm,B=(b)mxn为两个同型矩阵 矩阵加法定义为A+B=(a十b)mxm,A+B称为 A与B的和. 交换律 A+B=B+A 结合律 (A+B)+C=A+(B+C) 设A=(a),记-A=(-a),-A称为矩阵A的 负矩阵，从而有A+(-A)=O,并规定 A-B=A+(-B)

. ( ) , ( ) , ( ) , 与 的 和 矩阵加法定义为 称 为 设 为两个同型矩阵 A B A B a b A B A a B b ij ij m n ij m n ij m n + = + + = =    交换律 结合律 ５ 矩阵相加 ( ). , ( ) , ( ), ( ), A B A B A A O A aij A aij A A − = + − + − = = − = − − 负矩阵 从而有 并规定 设 记 称为矩阵 的 A+ B = B + A (A+ B) + C = A+ (B + C)

6 数乘矩阵 数几与矩阵A的乘积记作孔A或A几，规定为 2A=A2=(2a) 运算规律 (2μ)A=2(A)； (2+四)A=2A+A; 2(A+B)=2A+2B. 区回

( ). , A A a A A A    ij    = = 数 与矩阵 的乘积记作 或 规定为 运算规律 ()A = (A); ( + )A = A+ A; (A+ B) = A+ B. ６ 数乘矩阵

7 矩阵相乘 设A=(a时)mxs,B=(b)xn,规定A与B的乘积 是一个m×n矩阵C=(c)mxn,其中 cg-anby+aiba++asby-Eanby (i=1,2,.,m;j=1,2,.n) 记作 C=AB. 上页

. ( 1,2, , ; 1,2, ), ( ) , ( ) , ( ) , 1 1 1 2 2 C AB i m j n c a b a b a b a b m n C c A a B b A B s k ij i j i j is sj ik k j ij m n ij s n ij m s = = = = + + + =   = = = =    记 作 是一个 矩 阵 其 中 设 规 定 与 的乘积    ７ 矩阵相乘