《高等数学》课程教学资源（PPT课件）第三章微分中值定理与导数的应用_第二节洛必达法则

第二节洛必达法则 一、8 型未定式 二、 型未定式 三、其他未定式 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 洛必达法则 一、 型未定式 二、 型未定式 三、其他未定式 0 0  

第二节洛必达法则 一、8 型未定式 定理1设 (1)limf(x)=lim F(x)=0; x->a x→a (2)在点a的某去心邻域内，f'x)及F'x)都存在， 且F'c)≠0 f'(x) 3)1imF'() 存在（或为无穷大）， x->a 那么 f f'(x) 洛必达法则 x->a =limF() x->a 证明白 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 洛必达法则 定理1 设 一、 0 型未定式 0 (1) ( ) ( ) 0 ; lim = lim = → → f x F x x a x a (2) 在点 a 的某去心邻域内，f (x) 及 F (x) 都存在， 且 F (x)  0； (3) ( ) ( ) lim F x f x x a   → 存在(或为无穷大)， 那么 . ( ) ( ) ( ) ( ) lim lim F x f x F x f x x a x a   = → → 洛必达法则 第二节 洛必达法则 证明 因为在求极限 ( ) ( ) lim F x f x x→a 时，极限是否存在与 f (x) 及 F(x) 在 x = a 处有无定义无关，故可令 f (a) = 0 , F(a) = 0 . 设 x 是该邻域内的一点，则 f (x) 及 F(x) 在 以 x 及 a 为端点的区间上满足柯西中值定理的条件，于 是有 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )   F f F x F a f x f a F x f x   = − − = ( 在 x 与 a 之间). 所以 ( ) ( ) lim F x f x x→a ( ) ( ) lim   F f x a   = → ( ) ( ) lim    F f a   = → . ( ) ( ) lim F x f x x a   = → 证毕

第二节洛必达法则 几点说明 (1)定理中的x→a可以改成其他变化过程； a若im 仍属。 型，则可继续施用洛必达法 x->a 则，即 f(x) im f"(x) x->a x-→a ' (③)若lim 不存在，只能说明该极限不能用洛 达法则来计算，而不能断定原极限也不存在 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 洛必达法则 几点说明 (1) 定理中的 x→a 可以改成其他变化过程； (2) 若 ( ) ( ) lim F x f x x a   → 仍属 0 0 型，则可继续施用洛必达法 则，即 ; ( ) ( ) ( ) ( ) ( ) ( ) lim lim lim F x f x F x f x F x f x x a x a x a   =   = → → → (3) 若 ( ) ( ) lim F x f x x a   → 不存在，只能说明该极限不能用洛 达法则来计算，而不能断定原极限也不存在

第二节洛必达法则 x3-3x+2 例1求limx-x-x+1 x->l 解 x-Sinx 例2求lim X0 解 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 第二节 洛必达法则 洛必达法则 解 例1 求 . 1 3 2 3 2 3 1 lim − − + − + → x x x x x x       型 0 0 1 3 2 3 2 3 1 lim − − + − + → x x x x x x 3 2 1 3 3 2 2 1 lim − − − = → x x x x       型 0 0 6 2 6 lim 1 − = → x x x (不是未定型) . 2 3 = 注意 6 2 6 lim →1 x − x x 不能再用洛必达法则. 例1 求 . 1 3 2 3 2 3 1 lim − − + − + → x x x x x x 第二节 洛必达法则 解       型 0 0 3 0 sin lim x x x x − → 2 0 3 1 cos lim x x x − = →       型 0 0 x x x 6 sin lim →0 = . 6 1 = 例2 求 . sin 3 0 lim x x x x − 例 → 2 求 . sin 3 0 lim x x x x − →

第二节洛必达法则 二、∞ 型未定式 定理2设 (1)limf(x)=limF(x)=; X→a (2)在点a的某去心邻域内，f'x)及F'x)都存在， 且F'c)≠0； (3)lim f'(x) x->a F'(x) 存在（或为无穷大）， 那么 lim X→a F(x) =imF网 f'(x) 洛必达法则 x→a 证明略. 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 洛必达法则 定理2 设 二、  型未定式  (1) ( ) ( ) ; lim = lim =  → → f x F x x a x a (2) 在点 a 的某去心邻域内，f (x) 及 F (x) 都存在， 且 F (x)  0； (3) ( ) ( ) lim F x f x x a   → 存在(或为无穷大)， 那么 . ( ) ( ) ( ) ( ) lim lim F x f x F x f x x a x a   = → → 洛必达法则 证明略

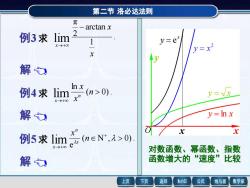
第二节洛必达法则 元 arctan x 例3求lim 2 X-→+0 y=x X 解 In x 例4求lim (n>0) X)+00 X 解 y=Inx 例5求im若meNA>0). x)+0 对数函数、幂函数、指数 解 函数增大的“速度”比较 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 第二节 洛必达法则 洛必达法则 解       型 0 0 例3 求 . 1 arctan 2 π lim x x x − →+ x x x 1 arctan 2 π lim − →+ 2 2 1 1 1 lim x x x − + − = →+ 2 2 1 lim x x x + = →+         型 x x x 2 2 lim →+ = =1. 例3 求 . 1 arctan 2 π lim x x x − →+ 第二节 洛必达法则 解 例4 求 ( 0). ln lim  →+ n x x n x         型 n x x ln x lim →+ 1 1 lim − →+ = n x nx x n x nx 1 lim →+ = = 0 . 例4 求 ( 0). ln lim  →+ n x x n x 第二节 洛必达法则 解         例5 求 ( N , 0) . 型 e lim   + →+   n x x n x x n x x  e lim →+ x n x nx  e 1 lim − →+ = x n x n n x   e ( 1) 2 2 lim − →+ − = = n x x n   e ! lim →+ = = 0 . 例5 求 ( N , 0). e lim   + →+   n x x n x 对数函数、幂函数、指数 函数增大的“速度”比较 x y x y = ln x y = x 2 y = x x y = e O

第二节洛必达法则 三、其他未定式 其他未定式有 0.00,0-00,00,1°，00 这些不定式要么可以转化成。 型，要么可以转化成 型 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 洛必达法则 三、其他未定式 其他未定式有 0 0 0, − , 0 ,1 ,   这些不定式要么可以转化成 0 0 型，要么可以转化成   型

第二节洛必达法则 例6求limx"hx(n>0) x→0 解 y=x"Inx 例7求lim(secx-tanx). y=sec x-tanx 解 1习 例8求limx x→01 解包 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 第二节 洛必达法则 洛必达法则 解 例6 求 ln ( 0). (0型) lim 0  → + x x n n x x x n x ln lim 0 → + n x x x − → + = ln lim 0         型 1 0 1 lim − − → − = + n x nx x n x n x − = → + lim 0 = 0 . 不能转化成 0 0 型. 例6 求 ln ( 0). lim 0  → + x x n n x 第二节 洛必达法则 解 例7 求 (sec tan ). ( − 型) lim 2 π x x x − → (sec tan ) lim 2 π x x x − →       = − → x x x x cos sin cos 1 lim 2 π x x x cos 1 sin lim 2 π − = →       型 0 0 x x x sin cos lim 2 π − − = → = 0 . 例7 求 (sec tan ). lim 2 π x x x − → 第二节 洛必达法则 解 ( 型) 0 例8 求 lim . 0 0 x x x → + x x x lim 0 → + x x x ln 0 e lim → + = 而 x x x ln lim 0 → + (0型) 1 0 ln lim − → + = x x x         型 2 0 1 lim − → − = + x x x x x lim 0 → + = − = 0 . 所以 x x x lim 0 → + e 1. 0 = = 例8 求 . lim 0 x x x → + y x x n = ln x y O y = sec x − tan x x y O x y = x x y O

第二节洛必达法则 例9求lim tanx-x x-0 解 例10求lim V1+x2 x→+00 X 解 x+sinx 例11求lim X→ 解 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 第二节 洛必达法则 洛必达法则 解       型 0 0 例9 求 . sin tan 2 0 lim x x x x x − → 本题当然可以直接用洛必达法则，但计算很繁琐 先把分母用等价无穷小代换： 2 3 x sin x ~ x 可以优化计算. x x x x x sin tan 2 0 lim − → 3 0 tan lim x x x x − = →       型 0 0 2 2 0 3 sec 1 lim x x x − = →       型 0 0 x x x x 6 2sec tan 2 0 lim → =       型 0 0 x x x x tan 3 sec2 0 = lim  → . 3 1 = 例9 求 . sin tan 2 0 lim x x x x x − → 第二节 洛必达法则 解 很多时候用洛必达法则求极限确实非常有效，但也 有些极限不能用洛必达法则求解. 例10 求 . 1 2 lim x x x + →+         型 x x x 2 1 lim + →+ 2 1 lim x x x + = →+ . 1 2 lim x x x + = →+ 本例就属于此情形. x x x 2 1 lim + →+ 2 1 1 lim x x = + →+ =1. 例10 求 . 1 2 lim x x x + →+ 第二节 洛必达法则 解         型 x x x x sin lim + → (1 cos ) lim x x = + → 例11 求 . sin lim x x x x + → 不存在. 所以不能用洛必达法则求解. x x x x sin lim + →       = +  → x x x sin 1 1 lim =1. 例11求 . sin lim x x x x + →