《高等数学》课程教学资源（PPT课件）第一章函数与极限_第七节无穷小的比较

第七节无穷小的比较 一、无穷小的阶 二、无穷小等价的条件 三、利用等价无穷小求极限 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 无穷小的比较 一、无穷小的阶 二、无穷小等价的条件 三、利用等价无穷小求极限

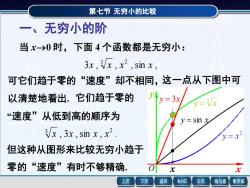
第七节无穷小的比较 一、无穷小的阶 当x→0时，下面4个函数都是无穷小： 3x,x,x2,sin x, 可它们趋于零的“速度”却不相同，这一点从下图中可 以清楚地看出.它们趋于零的 yly=3x y=Vx “速度”从低到高的顺序为 y=sin x x ,3x,sin x,x2. y=x2 但这种从图形来比较无穷小趋于 零的“速度”有时不够精确。 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 无穷小的比较 一、无穷小的阶 当 x→0 时，下面 4 个函数都是无穷小： 3 , , , sin , 3 2 x x x x 可它们趋于零的“速度”却不相同，这一点从下图中可 以清楚地看出. y = 3x 3 y = x 2 y = x y = sin x x x y O 它们趋于零的 “速度”从低到高的顺序为 , 3 , sin , . 3 2 x x x x 但这种从图形来比较无穷小趋于 零的“速度”有时不够精确

第七节无穷小的比较 x ,3x,sin x,x2 精确的方法是：用比值的极限来恒量它们趋于零的 “速度” 3x lim =0,所以趋于零的“速度”3x比“快”； x-→0 sin x 1 lim 所以趋于零的“速度”sinx与3x“相仿”； x→0 3x lim =0,所以趋于零的“速度”x2比sinx“快” →0 sin x 下面引进无穷小的阶，用来恒量趋于零的“速度” 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 无穷小的比较 “相仿”; 精确的方法是：用比值的极限来恒量它们趋于零的 “速度”. , 3 , sin , . 3 2 x x x x 0 , 3 3 0 lim = → x x x 所以趋于零的“速度” 3 3x 比 x “快”； , 3 1 3 sin lim 0 = → x x x 所以趋于零的“速度” sin x 与 3x 0 , sin 2 0 lim = → x x x 所以趋于零的“速度” sin x 2 x 比 “快”. 下面引进无穷小的阶，用来恒量趋于零的“速度

第七节无穷小的比较 定义设lima=0,limB=0, 如果lim P=0,就说B是比a高阶的无穷小，记作 B=o(a);如果im E_o,就说B是比a低阶的无穷小 如果im E=c+0,就说B与a是同阶的无穷小 如果 lim =c*0,k>0, B 就说B是关于a的k阶 的无穷小 如果lim B-=1,就说B与a是等价无穷小，记作 a~B 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 无穷小的比较 定义 设 lim  = 0 , lim  = 0 , 如果 lim = 0 ,   就说  是比  高阶的无穷小，记作  = o() ; 如果 lim =  ,   就说  是比  低阶的无穷小. 如果 lim = c  0 ,   就说  与  是同阶的无穷小； 如果 lim = c  0 , k  0 , k   的无穷小. 就说  是关于  的 k 阶 如果 lim = 1,   就说  与  是等价无穷小，记作  ~ 

第七节无穷小的比较 x ,3x,sin x,x2. 由定义可知，前面讨论过的上述4个无穷小中 x是比3x低阶的无穷小： 3x与sinx是同阶无穷小； x2是比sinx高阶的无穷小； x2是关于sinx2阶的无穷小. 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 无穷小的比较 , 3 , sin , . 3 2 x x x x 由定义可知， 前面讨论过的上述4个无穷小中 3 x 3x sin x 2 x 是比 低阶的无穷小； 3x 与 是同阶无穷小； 是比 sin x 高阶的无穷小； 2 x 是关于 sin x 2阶的无穷小

第七节无穷小的比较 例1证明：当x0时，1+x-1~1x 证明 例2证明：当x→0时，e-1~x. 证明 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 无穷小的比较 例1 证明：当 x→0 时， 第七节 无穷小的比较 证明 例1 证明：当 x→0 时， . 1 1 1 ~ x n x n + − 令 1 x 1 t , n + − = 则 = ( +1) −1, n x t 且 x→0 时 t→0 . 于是 x n x n x 1 1 1 lim 0 + − → ( 1) 1 lim 0 + − = → n t t nt 1 1 2 2 0 lim + + + + − = → n n t n n nt C t C t nt  =1. 所以 . 1 1 1 ~ x n x n + − . 1 1 1 ~ x n x n + − 例2 证明：当 x→0 时， 第七节 无穷小的比较 证明 例2 证明：当 x→0 时， 令 e 1 t , x − = 则 x = ln(t +1) , 且 x→0 时 t→0 . 于是 x x x e 1 lim 0 − → ln( 1) lim 0 + = → t t t ln(1 ) 1 1 lim 0 t t t + = → 所以 e 1~ x . x − t t t 1 0 ln(1 ) 1 lim + = → ln e 1 = =1. e 1~ x . x − e 1~ x . x −

第七节无穷小的比较 二、无穷小等价的条件 定理1B与是等价无穷小的充分必要条件是 B=a+o(a). 证明 常见的等价无穷小 当x→0时， sin x~x,tan x~x,arcsin x~x,arctanx~x,e*-1~x, 1+x)≈x,1=cosx。X21+x=18 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 无穷小的比较 二、无穷小等价的条件 定理1  与  是等价无穷小的充分必要条件是  =  + o( ). 第七节 无穷小的比较 证明 定理1  与  是等价无穷小的充分必要条件是  =  + o( ). 必要性 设  ~  , 即 lim =1,   则   − lim       = lim −1   = lim −1   = 0 , 因此  –  = o( )，即  =  + o( ). 充分性 设  =  + o( )，则   lim   () lim + o =       = +  () lim 1 o =1, 因此  ~  . 证毕 常见的等价无穷小 当 x→0 时， sin x ~ x , tan x ~ x , arcsin x ~ x , arctan x ~ x , e 1 ~ x , x − ln(1+ x) ~ x , , 2 1 1 cos ~ 2 − x x . 1 1 1 ~ x n x n + −

第七节无穷小的比较 三、利用等价无穷小求极限 定理2设a~',B~B',且lm 存在，则 lim O 证明 sin 2x 例如，lim lim x2 sin 5x x-→0 x→0 5x -5 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 无穷小的比较 三、利用等价无穷小求极限 定理2 设  ~  ,  ~   , 且     lim 存在，则 lim lim .       = 第七节 无穷小的比较 证明 证毕 定理2 设  ~  ,  ~  , 且     lim 存在，则 lim lim .       =   lim               =       lim             = lim lim lim lim .     = 例如， x x x sin 5 sin 2 lim →0 x x x 5 2 lim →0 = . 5 2 =

第七节无穷小的比较 tan x-sin x 例3求lim x0 解 例4求 /1+x2-1 lim x→0 cosx-1 解 例5证明当x0+时，h1+xV A1-/x 证明 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 无穷小的比较 例3 求 . tan sin 3 0 lim x x x x − → 第七节 无穷小的比较 解 例3 求 . tan sin 3 0 lim x x x x − → 3 0 tan sin lim x x x x − → 3 0 (1 cos )tan lim x x x x − = → 3 2 0 2 1 lim x x x x  = → . 2 1 = 例4 求 . cos 1 1 1 4 2 0 lim − + − → x x x 第七节 无穷小的比较 解 例4 求 . cos 1 1 1 4 2 0 lim − + − → x x x cos 1 1 1 4 2 0 lim − + − → x x x 2 2 0 2 1 4 1 lim x x x − = → . 2 1 = − 例5 证明当 x→0 +时， ~ . 1 1 ln x x x − + 第七节 无穷小的比较 证明 例5 证明当 x→0 + 时， ~ . 1 1 ln x x x − + 因为 ln(1 ) ln(1 ) , 1 1 ln x x x x = + − − − + 而 ln(1+ x) ~ x , ln(1− x) ~ − x , 由定理2得 ln(1+ x) = x + o(x) , ln(1− x) = − x + o(− x) , 于是 ln(1 ) ln(1 ) 1 1 ln x x x x = + − − − + = x + x + o(x) − o(− x) , 所以 x x x x − + → + 1 1 ln lim 0 x x x o x o x x ( ) ( ) lim 0 + + − − = → + =1. ~ . 1 1 ln x x x − + 即