《高等数学》课程教学资源（课件讲稿）高等数学2.5

第五节 第二章 离教的微分 一、微分的概念 二、微分运算法则 三、微分在近似计算中的应用 四、微分在估计误差中的应用 HIGH EDUCATION PRESS

二、微分运算法则 三、微分在近似计算中的应用 四、微分在估计误差中的应用 第五节 一、微分的概念 机动 目录 上页 下页 返回 结束 函数的微分 第二章

一、 微分的概念 引例：一块正方形金属薄片受温度变化的影响，其 边长由x变到x。+Dx,问此薄片面积改变了多少？ 设薄片边长为x,面积为A,A=x2,当x在取 得髫量Dx时，面积的增量为 DA=(0+Dx)2-x2 XoDx Dx 2xoDx+(Dx) 关于△x的 Dx®O时为 xo A=话 线性主部 高阶无穷小 故 DA》2xDx 称为函数在xo的微分 HIGH EDUCATION PRESS 结

一、微分的概念 引例: 一块正方形金属薄片受温度变化的影响, 问此薄片面积改变了多少? 设薄片边长为 x , 面积为 A , 则 面积的增量为 关于△x 的 线性主部 高阶无穷小 时为 故 称为函数在 的微分 当 x 在 取 得增量 时, 边长由 变到 其 机动 目录 上页 下页 返回 结束

定义：若函数y=f(x)在点xo的增量可表示为 Dy=f(xo +Dx)-f(xo)=ADx+o(Dx) (A为不依赖于△x的常数) 则称函数y=f(x)在点x可微，而ADr称为f(x)在 点x的微分，记作dy或df,即 dy=ADx 定理：函数y=f(x)在点xo可微的充要条件是 y=f(x)在点xo处可导，且A=fx),即 dy=ffxo)Dx HIGH EDUCATION PRESS 结球

的微分, 定义: 若函数 在点 的增量可表示为 ( A 为不依赖于△x 的常数) 则称函数 而 称为 记作 即 定理: 函数 在点 可微的充要条件是 即 在点 可微, 机动 目录 上页 下页 返回 结束

定理：函数y=(x)在点xo可微的充要条件是 y=f(x)在点xo处可导，且A=f4xo),即 dy fxo)Dx 证：“必要性” 已知y=f(x)在点x可微，则 Dy=f(xo +Dx)-f(xo)=4Dx+o(Dx) 4+- Dx®ODx D®O 故y=f(x)在点x的可导，且f4xo)=A HIGH EDUCATION PRESS

定理 : 函数 证: “必要性” 已知 在点 可微 , 则 故 在点 的可导, 且 在点 可微的充要条件是 在点 处可导, 且 即 机动 目录 上页 下页 返回 结束

定理：函数y=f(x)在点xo可微的充要条件是 y=f(x)在点x,处可导，且A=f4x),即 dy=fxo)Dx “充分性 已知y=f(x)在点x的可导，则 99 lim Dy=faxo) Dx®ODX Dy=fAxo)+a（ lim a =0) D Dx®O 故 Dy=fx)Dx+aDx=1oDe) 线性主部 (f4xo)'0时) 即dy=fxo)Dx HIGH EDUCATION PRESS 结球

定理 : 函数 在点 可微的充要条件是 在点 处可导, 且 即 “充分性 ” 已知 即 在点 的可导, 则 机动 目录 上页 下页 返回 结束

说明：Dy=4x)Dx+o(Dx) dy=fxo)Do 当f4xo)0时， lim Dy Dy lim D0dy Dx®0f4xO)Dx lim Dy =】 fdxo) x®ODX 所以Dx®O时Dy与dy是等价无穷小，故当Dx 很小时，有近似公式 Dy》dy HIGH EDUCATION PRESS 返回 结

说明: 时 , 所以 时 很小时, 有近似公式 与 是等价无穷小, 当 故当 机动 目录 上页 下页 返回 结束

微分的几何意义— 切线纵坐标的增量 dy fxo)Dx tana XDx d y=f(x) 当Dx很小时，Dy》dy 当y=x时， Dy=De dx 称Dx为自变量的微分，记作dc 0+D 则有 dy=fex)dx 从而 导数也叫作微商 dx HIGH EDUCATION PRESS 结

微分的几何意义 当 很小时, 则有 从而 导数也叫作微商 切线纵坐标的增量 自变量的微分, 记作 记 机动 目录 上页 下页 返回 结束

例2，y=x3 dy x=2 3x2 xdx x=2 =0.24 dx=0.02 dx=0.02 又如，y=arctanx, dy-,1adx 1+x HIGH EDUCATION PRESS 目录 结球

例2, 又如, 机动 目录 上页 下页 返回 结束

二、微分运算法则 设(x),v(x)均可微，则 1.d(士y)=du±d 2.d(C)=Cd(C为常数) 3.d(uv)vdu +udv (y10 5.复合函数的微分 y=f(),u=j(x)分别可微， 则复合函数y=)(x)]的微分为 dy=ygdx=fu方x)dx→☑ dy fdu)du 微分形式不变 HIGH EDUCATION PRESS 结

二、 微分运算法则 设 u(x) , v(x) 均可微 , 则 (C 为常数) 分别可微 , 的微分为 微分形式不变 5. 复合函数的微分 则复合函数 机动 目录 上页 下页 返回 结束

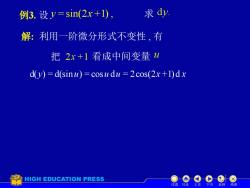
例3.设y=sin(2x+1), 求dy 解：利用一阶微分形式不变性，有 把2x+1看成中间变量4 d(y)=d(sinu)=cosu du =2cos(2x+1)dx HIGH EDUCATION PRESS 返回 结球

例3. 设 求 解: 利用一阶微分形式不变性 , 有 注意 目录 上页 下页 返回 结束 把 看成中间变量