《高等数学》课程教学资源（PPT课件）高等数学7.2 可分离变量微分方程

第二节 第七章 可分离变量微分方程 可分离变量方程 =f(x)f) dx M (x)M2(y)dx+N(x)N2(y)dy=0 转化 解分离变量方程g(y)dy=f(x)dx HIGH EDUCATION PRESS 机动目录上页下页返回结束

转化 可分离变量微分方程 机动 目录 上页 下页 返回 结束 第二节 解分离变量方程 g(y)dy = f (x)dx 可分离变量方程 ( ) ( ) d d 1 2 f x f y x y = M1 (x) M (y) dx + N 1 (x) N (y)d y = 0 2 2 第七章

分离变量方程的解法： g(y)dy=f(x)dx ① 设y=p(x)是方程①的解，则有恒等式 g((x))o'(x)dx=f(x)dx 两边积分，得 ∫gy)dy=∫f(x)dx G(y) F(x) 则有 G(y)=F(x)+C 当G6)与Fx)可微且Gy)=gy0时，上述过程可逆 说明由②确定的隐函数y=x)是①的解.同样，当F'(x) =f(x)0时，由②确定的隐函数x=y)也是①的解 称②为方程①的隐式通解，或通积分 HIGH EDUCATION PRESS 机动目录上页下页返回结束

分离变量方程的解法: g(y)dy = f (x)dx 设 y＝ (x) 是方程①的解, g( (x))(x)dx  f (x)dx 两边积分, 得 f (x)dx  = ① 则有恒等式 ② 当G(y) 与F(x) 可微且 G’(y) ＝g(y)≠0 时, 说明由②确定的隐函数 y＝(x) 是①的解. 则有 称②为方程①的隐式通解, 或通积分. 同样,当F’(x) = f (x)≠0 时, 上述过程可逆, 由②确定的隐函数 x＝(y) 也是①的解. 机动 目录 上页 下页 返回 结束

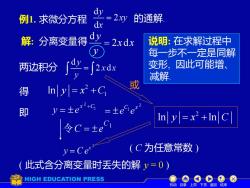
例1.求微分方程 dy =2xy 的通解 解：分离变量得 2xdx 说明：在求解过程中 1 每—步不一定是同解 两边积分 -2 变形，因此可能增、 减解 得 Iny =x2+C 或 即 y=±e+G =±e9e In y =x2+In C 令C=±eC1 v=Ce (C为任意常数)》 此式含分离变量时丢失的解y=0) HIGH EDUCATION PRESS 机动目 下页返回结束

例1. 求微分方程 的通解. 解: 分离变量得 d 2 d y x x y = 两边积分 得 2 1 ln y x C = + 2 即 ln ln y x C = + C1 令C = e ( C 为任意常数 ) 或 说明: 在求解过程中 每一步不一定是同解 变形, 因此可能增、 减解. ( 此式含分离变量时丢失的解 y = 0 ) 机动 目录 上页 下页 返回 结束

xydx+(x2+1)dy =0 例.解初值问题 0)=1 解：分离变量得 X 2 dx 1+x1 两边积分得lny=ln x2+1 +1nC 即 yx2+1=C(C为任意常数) 由初始条件得C=1,故所求特解为 yx2+1=1 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例. 解初值问题 d ( 1) d 0 2 xy x + x + y = 解: 分离变量得 x x x y y d 1 d 2 + = − 两边积分得 即 y x +1 = C 2 由初始条件得 C = 1, 1 1 2 y x + = ( C 为任意常数 ) 故所求特解为 y(0) =1 机动 目录 上页 下页 返回 结束

练习：求方程 dy= 的通解 d 解分离变量 e dy=ex dx -e=ex+C 即 (e+C)ey+1=0(C<0） HIGH EDUCATION PRESS 机动目录上页下页返回结束

练习: 解 分离变量 e e C y x − = + − 即 ( + ) +1 = 0 x y e C e ( C < 0 ) 机动 目录 上页 下页 返回 结束

例2.已知放射性元素铀的衰变速度与当时未衰变原 子的含量M成正比，已知t=0时铀的含量为Mo,求在 衰变过程中铀含量M()随时间t的变化规律 dM dt =-元M(元>0) 解：根据题意，有 M,0=M,(初始条件) 对方程分离变量，然后积分 -j(-ar 得lnM=-t+lnC,即M=Ce2t ↑M 利用初始条件，得C=M0 M 故所求铀的变化规律为M=Moe2 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例2. 子的含量 M 成正比, 求在 衰变过程中铀含量 M(t) 随时间 t 的变化规律. 解: 根据题意, 有 ( 0) d d = − M   t M M t=0 = M0 (初始条件) 对方程分离变量, 得 ln M = − t + lnC, 即 t M Ce − = 利用初始条件, 得 C = M0 故所求铀的变化规律为 . 0 t M M e − = M M0 t o 然后积分:   已知 t = 0 时铀的含量为 已知放射性元素铀的衰变速度与当时未衰变原 机动 目录 上页 下页 返回 结束

例3.设降落伞从跳伞塔下落后所受空气阻力与速度 成正比，并设降落伞离开跳伞塔时(t=0)速度为0，求 降落伞下落速度与时间的函数关系 解：根据牛顿第二定律列方程m mg-kv dt 初始条件为V=0=0 方鸡分安显然怎税盼了产、 得 -是n(mg-k)=+C(此处mg-kr>0) 利用初始条件，得C=-ln(mg) t足够大时 V≈g 代入上式后化简，得特解v= mg(1-e m HIGH EDUCATION PRESS 机动目录上页下页返回结束

例3. 成正比, 求 解: 根据牛顿第二定律列方程 = t v m d d 初始条件为 v t=0 = 0 对方程分离变量, 然后积分   : 得 (此处 mg − kv  0) 利用初始条件, 得 ln ( ) 1 mg k C = − 代入上式后化简, 得特解 并设降落伞离开跳伞塔时( t = 0 ) 速度为0, (1 ) t m k e k m g v − = − mg − kv 设降落伞从跳伞塔下落后所受空气阻力与速度 降落伞下落速度与时间的函数关系. k mg v  t 足够大时 机动 目录 上页 下页 返回 结束

例4.有高1m的半球形容器，水从它的底部小孔流出， 小孔横截面积S=1cm2开始时容器内盛满了水，求水 从小孔流出过程中，容器里水面的高度h随时间t的变 化规律 解：由水力学知，水从孔口流出的流量为 d dr-0. 100cm 流量系数 孔口截面面积 重力加速度 h+dh 即 dV =0.62,/2ghdt 设在[t,t+dt]内水面高度由h降到h+dh(dh<0) HIGH EDUCATION PRESS 0e0C①8 机动目录上页下页返回结束

100cm 例4. 有高 1m 的半球形容器, 水从它的底部小孔流出, 开始时容器内盛满了水, 从小孔流出过程中, 容器里水面的高度 h 随时间 t 的变 r 解: 由水力学知, 水从孔口流出的流量为 即 dV = 0.62 2gh d t 小孔横截面积 求水 化规律. 流量系数 孔口截面面积 重力加速度 设在 内水面高度由 h 降到h + d h (d h  0), h + d h h h o 机动 目录 上页 下页 返回 结束

对应下降体积 dW=-πr2dh r=V1002-(100-h)2=200h-h dV=-π(200h-h2)dh h 因此得微分方程定解问题： 100cm 0.62/2ghdt=-π(200h-h2)dh h+dh h=0=100 将方程分离变量： dt=- (200%-h产)ah 0.622g HIGH EDUCATION PRESS 机动目 下页返回结束

100cm r h + d h h h o 对应下降体积 dV r dh 2 = − 2 2 r = 100 − (100 − h) 2 = 200h − h dV (200h h )dh 2 = − − 因此得微分方程定解问题: 将方程分离变量: h h h g t (200 )d 0.62 2 d 2 3 2 1 = − −  机动 目录 上页 下页 返回 结束

两端积分，得 π t=- 062V2 ∫(200h-h之)dh 100cm π o h+dh 0.62、/2g 利用初始条件，得C= 元 14 =0=100 105 0.622g15 因此容器内水面高度h与时间t有下列关系 π (7×103-103h7+3h2) 4.652g HIGH EDUCATION PRESS 机动目录上页下页返回结束

g t 0.62 2  = − 两端积分, 得 0.62 2g  = − ( 200h h )dh 2 3 2 1 −  2 3 3 400 ( h ) 5 2 2 5 − h +C 利用初始条件, 得 5 10 15 14 0.62 2 =   g C  因此容器内水面高度 h 与时间 t 有下列关系: (7 10 10 3 ) 4.65 2 2 5 2 3 5 3 h h g t =  − +  h t =0 =100 100cm r h + d h h h o 机动 目录 上页 下页 返回 结束