《高等数学》课程教学资源（课件讲稿）高等数学5.1

第五章 定积分 不定积分 积分学 定积分

第五章 积分学 不定积分 定积分 定积分

第一为 第五章 定积分的桡念及性质 一、定积分问题举例 二、定积分的定义 三、定积分的性质 HIGH EDUCATION PRESS 自录 结

第一节 一、定积分问题举例 二、 定积分的定义 三、 定积分的性质 机动 目录 上页 下页 返回 结束 定积分的概念及性质 第五章

一、定积分问题举例 矩形面积=an h 梯形面积=(a+b) 1.曲边梯形的面积 设曲边梯形是由连续曲线 y=f(x)(f(x)30) 及x轴，以及两直线x=a,x=b 所围成，求其面积A: HIGH EDUCATION PRESS 结球

一、定积分问题举例 1. 曲边梯形的面积 设曲边梯形是由连续曲线 以及两直线 所围成 , 求其面积 A . 机动 目录 上页 下页 返回 结束 矩形面积 梯形面积

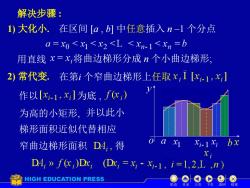
解决步骤： 1)大化小.在区间[a,b]中任意插入n-1个分点 a=x0<x1<x2<L <xn-1<xn=b 用直线x=x,将曲边梯形分成n个小曲边梯形 2)常代变，在第i个窄曲边梯形上任取x,1【x-1,x,] 1 作以[x-1,x]为底，fc,) 为高的小矩形，并以此小 梯形面积近似代替相应 窄曲边梯形面积DA,得 o a x xi-1xi bx D4,》fGc,)Dx,(Dx,=x-x-1,i=1,2,L,n） HIGH EDUCATION PRESS n 结球

解决步骤 : 1) 大化小. 在区间 [a , b] 中任意插入 n –1 个分点 用直线 将曲边梯形分成 n 个小曲边梯形; 2) 常代变. 在第i 个窄曲边梯形上任取 作以 为底 , 为高的小矩形, 并以此小 梯形面积近似代替相应 窄曲边梯形面积 得 机动 目录 上页 下页 返回 结束

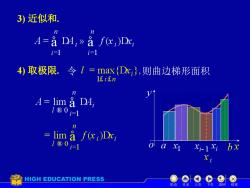
3)近似和. n n A=aDA,》afc,)Dx, i=1 i=1 4)取极限.令I=max {Dx,},则曲边梯形面积 IfiEn n A=lim a D4, 1®01 n lim a f(x)Dxi 1®01 o a x xi-1xi bx HIGH EDUCATION PRESS 结球

3) 近似和. 4) 取极限. 令 则曲边梯形面积 机动 目录 上页 下页 返回 结束

2.变速直线运动的路程 设某物体作直线运动，已知速度v=v(t)iCIT1,T2],且 v(t)30,求在运动时间内物体所经过的路程s. 解决步骤： 1)大化小.在[T,T2]中任意插入n-1个分点，将它分成 n个小段[t-1,t,0=1,2,L,n),在每个小段上物体经 过的路程为Ds,(i=1,2,L,) 2)常代变任取x,1[t-1,t,],以vc,)代替变速，得 Ds,》vc,)D,d=1,2,L,n HIGH EDUCATION PRESS 结

2. 变速直线运动的路程 设某物体作直线运动, 且 求在运动时间内物体所经过的路程 s. 解决步骤: 1) 大化小. 将它分成 在每个小段上物体经 2) 常代变. 得 已知速度 机动 目录 上页 下页 返回 结束 n 个小段 过的路程为

3)近似和. n s》avc;)Di i=1 4)取极限. n s lim a v;)Dt; (l max Dt;) 1®0 1 1E iEn 上述两个问题的共性： ·解决问题的方法步骤相同： “大化小，常代变，近似和，取极限 ·所求量极限结构式相同：特殊乘积和式的极限 HIGH EDUCATION PRESS 结球

3) 近似和. 4) 取极限 . 上述两个问题的共性: • 解决问题的方法步骤相同 : “大化小 , 常代变 , 近似和 , 取极限 ” • 所求量极限结构式相同: 特殊乘积和式的极限 机动 目录 上页 下页 返回 结束

二、定积分定义 设函数f(x)定义在[a,b]上，若对[a,b]的任一种分法 a=x0<<x2<L<xn=b,令Dx,=x,-x1,任取 x,i【x,x-il,只要1=max {Dx,}®0时afc)Dx lEiEn 1 总趋于确定的极限I,则称此极限I为函数f(x)在区间 [a,b]上的定积分，记作0f(x)dx f)dx=mf)Dv, 0x1 即 xiX bx 1®01 此时称f(x)在[a,b]上可积 HIGH EDUCATION PRESS 自录 返回 结

二、定积分定义 任一种分法 任取 总趋于确定的极限 I , 则称此极限 I 为函数 在区间 上的定积分, 即 此时称 f ( x ) 在 [ a , b ] 上可积 . 记作 机动 目录 上页 下页 返回 结束

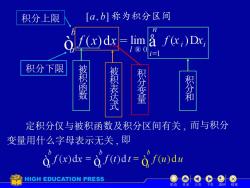
积分上限 [a,b]称为积分区间 olf(x)dx =lim a f(x,)Dx, i=l 积分下限 被积函数 被积表达式 积分变量 积分和 定积分仅与被积函数及积分区间有关，而与积分 变量用什么字母表示无关，即 d=di=fdu HIGH EDUCATION PRESS 结

积分上限 积分下限 被 积 函 数 被 积 表 达 式 积 分 变 量 积 分 和 定积分仅与被积函数及积分区间有关 , 而与积分 变量用什么字母表示无关 , 即 机动 目录 上页 下页 返回 结束

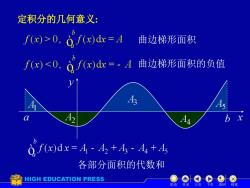
定积分的几何意义： J()>0,f(dx=A 曲边梯形面积 fx)<0,0/x)dr=-A 曲边梯形面积的负值 b 0,f(x)dx=A 42 +4s A+As 各部分面积的代数和 HIGH EDUCATION PRESS 自录 返回 结

定积分的几何意义: 曲边梯形面积 曲边梯形面积的负值 各部分面积的代数和 机动 目录 上页 下页 返回 结束