《高等数学》课程教学资源（PPT课件）高等数学1.6 极限存在准则及两个重要极限

第之节 第一章 极浪存在准则及 两个重要极限 极限存在准则 二、两个重要极限 HIGH EDUCATION PRESS 机动目录上页下页返回结束

二、 两个重要极限 一、极限存在准则 第六节 机动 目录 上页 下页 返回 结束 极限存在准则及 两个重要极限 第一章

准则 (1)yn≤xm≤2n(n=1,2,.) lim Xn a (2)lim yn lim zn a n->o0 n->o0 n→0 证：由条件(2)，V8>0,3N1,N2, 当n>N1时，yn-aN2时，2n-aV时，有 a-8c0 等HIGH EDUCATION PRESS 机动目录上页下页返回结束

y zn a n n n = = → → (2) lim lim 准则I (1) y  x  z ( n =1, 2, ) n n n xn a n = → lim 证:由条件 (2) ,   0, , N1 当 时, 当 时, 令 max , , N = N1 N2 则当 n  N 时, 有 由条件 (1) n n n a −  y  x  z  a + 即 x − a   , n 故 lim x a . n n = → , N2 机动 目录 上页 下页 返回 结束

函数极限存在的夹逼准则 准则1 当xeU(xo,6)时，g(x)≤f(x)≤hx), (x>X>0) 且 lim g(x)=lim h(x)=4 x→Xo X→X0 (x→0) (x→∞) lim f(x)=4 HIGH EDUCATION PRESS 机动目录上页下页返回结束

函数极限存在的夹逼准则 准则I′ ( , ) , 当x x0  时   g x h x A x x x x = = → → lim ( ) lim ( ) 0 0 g(x)  f (x)  h(x) , f x A x x = → lim ( ) 0 ( x  X  0) (x → ) (x → ) (x → ) 且 机动 目录 上页 下页 返回 结束

sin x 重要极限lim =1 x>0 X 证：当x∈(0，)时， △AOB的面积<圆扇形AOB的面积<△AOD的面积 即 2sinx<】x<tanx 故有 x< sinx cosx (0<x<) sinx 显然有 COS X< 1 (0<x<) X ~lim cosx=1,注 sinx lim =1 x-→0 →0 等HIGH EDUCATION PRESS 目录上页下页返回结束

1 sin cos   x x x 圆扇形AOB的面积 证: 当 即 sin x  2 1 tan x 2 1  亦即 sin tan (0 ) 2  x  x  x  x  (0, ) 2   x 时， (0 ) 2  显然有  x  △AOB 的面积＜ ＜△AOD的面积 D C B A x 1 o 故有 注 注 目录 上页 下页 返回 结束 重要极限

例1.求lim tan x x>0 解： lim tan x lim sinx 1 x→0 x-→0 x COSX nx lim- lim-=1 x→0X x-→0C0Sx 例2.求1im arcsin x x-→0 X 解：令t=arcsinx,则x=sint,因此 原式=lim t lim =1 t->0 sint t→0 sint HIGH EDUCATION PRESS 机动目录上页下页返回结束

例1. 求 解: x x x tan lim →0       = → x x x x cos sin 1 lim 0 x x x sin lim →0 = x cos x 1 lim →0  =1 例2. 求 解: 令 t = arcsin x, 则 x = sint , 因此 原式 t t t sin lim →0 = t sin t =1 机动 目录 上页 下页 返回 结束

例3.求lim 1-cosx x→0 x2 解：原式=12 x->0 -r月 说明：计算中注意利用 lim sin(x) =1 (x)-→0 (x) HIGH EDUCATION PRESS DeOC①8 机动目录上页下页返回结束

例3. 求 解: 原式 = 2 2 2 0 2sin lim x x x→ 2 1 2 1 =  说明: 计算中注意利用 2 0 sin lim       = x→ 2 x 2 x 2 1 机动 目录 上页 下页 返回 结束

2.单调有界数列必有极限（准则2） ≤x2≤.≤xn≤xn+1≤.≤M →>lim=a(≤M） n->oo X1 X2 Xnx a M 为1≥x2≥.≥Xn≥x+1≥.≥m >lim=b(≥m) n->o0 0 m h Xn+1Xn X2 X 证明略) HIGH EDUCATION PRESS 机动目录上页下页返回结束

2. 单调有界数列必有极限 ( 准则2 ) lim x a ( M ) n n =  → lim x b ( m ) n n =  → ( 证明略 ) a b 机动 目录 上页 下页 返回 结束

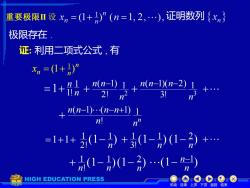
重要极限Ⅲ设xn=(1+)”(n=1,2,),证明数列{xn} 极限存在 证：利用二项式公式，有 xn=(0+” =1+易+mg+a2 21n21 3 +. 01 +nn-l):(n-n+1) 1 n! =1+1+2(1-月)+3(1-月)(1-分)+. +(1-)(1-分).(1-m） HIGH EDUCATION PRESS 机动目录上页下页返回结束

重要极限II 设 证明数列 极限存在 . 证: 利用二项式公式 , 有 n n n x (1 ) 1 = + =1+ n n 1 1! 2 1 2! ( 1) n n n− + 3 1 3! ( 1)( 2) n n n− n− + + n n n n n n n 1 ! ( −1) ( − +1) +  =1+1+ (1 ) 1 ! 1 n n + − (1 ) 2 n − (1 ) 1 n n−  − (1 ) 1 2! 1 n − (1 1 ) + 3! 1 n + − (1 ) 2 n − 机动 目录 上页 下页 返回 结束

xm=1+1+2(1-)+(1-分)(1-习)+. +(1-(1-a.(1-分） x=1+l+-+-)+. 大 大 +0-1-ma)(1-4 比较可知 x<xn+1(n=1,2,.） 又=0+”<1+1+分+++ HIGH EDUCATION PRESS 机动目录上页下页返回结束

xn =1+1+ (1 ) 1 ! 1 n n + − (1 ) 2 n − (1 ) 1 n n−  − (1 ) 1 2! 1 n − (1 1 ) + 3! 1 n + − (1 ) 2 n − xn+1 =1+1+ (1 ) 1 1 2! 1 + − n (1 )(1 ) 1 2 1 1 3! 1 + + + − − n n + (1 )(1 ) (1 ) 1 1 2 1 1 ( 1)! 1 + + + + + − − − n n n n n  大 大 正 ( 1, 2, ) xn  xn+1 n =  = (1+ ) 1+1+ 1 n n n 又 x 比较可知 机动 目录 上页 下页 返回 结束

又 xn=0+月)”oo e为无理数，其值为 e=2.718281828459045. HIGH EDUCATION PRESS 原题目录上页下页返回结束

根据准则 2 可知数列 xn 记此极限为 e , e n n n + = → lim(1 ) 1 e 为无理数 , 其值为 e = 2.718281828459045 即 有极限 . 原题 目录 上页 下页 返回 结束 = (1+ ) 1+1+ 1 n n n x 1+1+ 又  3 1 2 1 3 − = − n