《概率论与数理统计》课程教学课件（PPT讲稿，48学时）第二章 随机变量及其分布 第五节 随机变量的函数的分布

概率论与数理统外「 第五节随机变量的函数的分布 一、离散型随机变量的函数的分布 二、连续型随机变量的函数的分布

一、离散型随机变量的函数的分布 二、连续型随机变量的函数的分布 第五节 随机变量的函数的分布

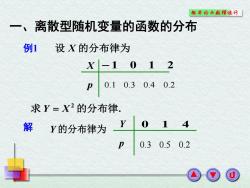
概率论与敖理统计】 一、离散型随机变量的函数的分布 例1设X的分布律为 X-1012 0.10.30.402 求Y=X2的分布律 解 Y的分布律为 Y 014 0.30.50.2

解 . 求 2 的分布律 设 的分布律为 Y X X  X p  1 0 1 2 0.1 0.3 0.4 0.2 例1 Y 的分布律为 Y p 0.3 0.5 0.2 0 1 4 一、离散型随机变量的函数的分布

概率论与散理统外「 离散型随机变量的函数的分布 如果X是离散型随机变量，其函数Y=g(X) 也是离散型随机变量若X的分布律为 X x x2 Xk Pe P P2 Pe 则Y=g(X)的分布律为 Y=g(X) 8(x1)8(x2) .8(xk) Pk P P2 Pk 若g(x)中有值相同的，应将相应的P合并

离散型随机变量的函数的分布 也是离散型随机变量 若 的分布律为 如果 是离散型随机变量 其函数 X X Y g X . ,  ( ) X pk x1 x2  xk  p1 p2  pk  则Y  g(X)的分布律为 pk Y  g(X) p1 p2  pk  g(x1 ) g(x2 )  g(xk )  若 ( )中有值相同的,应将相应的 合并. g xk pk

概率论与敖理统计】 二、连续型随机变量的函数的分布 例2 设随机变量X的概率密度为 x fx(x)= 0<x<4, 0,其他. 求随机变量Y=2X+8的概率密度

二、连续型随机变量的函数的分布 2 8 . 0, . , 0 4, ( ) 8 求随机变量 的概率密度 其他 设随机变量 的概率密度为          Y X x x f x X X 例2

概率论与散理统外」 例3设随机变量X的概率密度为fx(x),求随机变量 Y=X2的概率密度！ 解 先求随机变量Y=X2分布函数， 当y≤0时F(y)=0 当y>0时 F(Oy)=PY≤y}=P{X2≤y} =P{-y≤X≤V}=Fx(V)-Fx(-Vy)

F ( y) P{Y y} Y   { } 2  P X  y  P{ y  X  y} F ( y) F ( y)  X  X  2 ( ), . X f x X Y X  设随机变量 的概率密度为 求随机变量 的概率密度 解 , 先求随机变量 Y  X 2 分布函数 例3 当 y  0 时 当 y  0 时 FY ( y)  0

概率论与散理统外 再由分布函数求概率密度 Fx(Vy)-Fx(-) fy(y)=F(y) fx(W)(VPy'-f(-√少-√少)y,y>0 0, y≤0 6ni y≤0

f ( y) F ( y) Y Y   再由分布函数求概率密度. ( )( ) ( )( ) , 0 0, 0 X X f y y f y y y y            1 [ ( ) ( )] , 0 2 0, 0 X X f y f y y y y           F ( y ) F ( y ) X  X 

概率论与数理统外「 定理 设随机变量X具有概率密度fx(x), 其中-∞0(或恒有g'(x)<0),则称Y=g(X)是连续型 随机变量，其概率密度为 fx[h()h'(y),a<y<B, 0 其他 a=min(g(-oo),g(+oo)),B=max(g(-co),g(+o)), h(y)是g(x)的反函数

( ) ( ) . min( ( ), ( )), max( ( ), ( )), 是 的反函数 其中 h y g x α  g  g  β  g  g                    0, . [ ( )] ( ), , ( ) , ( ) 0( ( ) 0), ( ) , ( ) , ( ), 其他 随机变量 其概率密度为 或恒有 则称 是连续型 其中 又设函数 处处可导 且恒有 定理 设随机变量 具有概率密度 f h y h y α y β f y g x g x Y g X x g x X f x X Y X

概率论与散理统计 例4设随机变量X~N(4,o2),试证明X的线 性函数Y=X+b(a≠0)也服从正态分布. 证明X的概率密度为 x- fx(x)-J2no e 26,00<x<t. 设y=g(x)=x+b, 得x=)=’气，知)=+0

证明 X 的概率密度为 e , . 2π 1 ( ) 2 2 2 ( )        x σ f x σ x μ X 设 y  g(x)  ax  b, ( ) , a y b x h y  得   0. 1 ( )   a 知 h y ( 0) . ~ ( , ), 2 性函数 也服从正态分布 设随机变量 试证明 的线 Y  aX  b a  例4 X N μ σ X