《概率论与数理统计》课程教学课件（PPT讲稿，48学时）第五章 第二节 中心极限定理

概率纶与散理统针 §5.2中心极限定理 设{X,}为独立随机变量序列，记其和为 > 讨论独立随机变量和的极限分布 >指出极限分布为正态分布

§5.2 中心极限定理  讨论独立随机变量和的极限分布  指出极限分布为正态分布 设 {Xn} 为独立随机变量序列，记其和为 1 n k k X  

概率论与数理统外「 一、基本定理 定理四（独立同分布的中心极限定理) 设随机变量X1,X2,.,Xm,.相互独立，服从 同一分布，且具有数学期望和方差：E(X)=4, D(X)=o2>0(k=1,2,则随机变量之和的 2x-A2x x:-na 标准化变量Y,= k x Nno

一、基本定理 定理四（独立同分布的中心极限定理） 则随机变量之和的 同一分布 且具有数学期望和方差： 设随机变量 相互独立 服从 ( ) 0 ( 1,2, ), , ( ) , , , , , , 2 1 2        D X k E X X X X k k n                       n k k n k k n k k n D X X E X Y 1 标准化变量 1 1   n X n n k k   1

概率论与敖理统计「 的分布函数F,(x)对于任意x满足 ∑X-w lim F (x)=lim PK ≤X n→o no 定理四表明： 当n→o,随机变量序列Y,的分布函数收敛于 标准正态分布的分布函数

                    x n X n F x P F x x n k k n n n n   1 lim ( ) lim 的分布函数 ( ) 对于任意 满足 定理四表明: . , 标准正态分布的分布函数 当 n   随机变量序列 Yn 的分布函数收敛于     x t e dt (x). 2π 1 2 2 

概率论与散理统外「 例1一加法器同时收到20个噪声电压' (k=1,2,.20),设它们是相互独立的随机变量， 且都在K间Q10上服从均刻分布记业三% 20 求PV>105}的近似值

{ 105} . (0,1 0) , , ( 1,2, 2 0), , 2 0 20 1 求 的近似值 且都在区间 上服从均匀分布 记 设它们是相互独立的随机变量 一加法器同时收到 个噪声电压     P V V V k V k k k  例1

概率论与散理统计 定理五（李雅普诺夫中心极限定理） 设随机变量X1,X2,.,Xm,.相互独立，它 们具有数学期望和方差： E(Xk)=4k,D(Xk)=o2≠0(k=1,2, 记 B:-i, k=1 若存在正数6，使得当n→o时， 交4-

{| | } 0, 1 , , , ( ) , ( ) 0 ( 1,2, ), , , , , , 1 2 2 1 2 2 2 1 2                n k k k n n k n k k k k k n E X B n B E X D X k X X X        若存在正数 使得当 时 记 们具有数学期望和方差： 设随机变量 相互独立 它    定理五(李雅普诺夫中心极限定理)

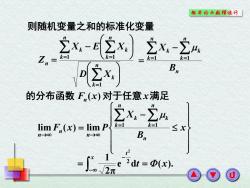
概率论与散理统外「 则随机变量之和的标准化变量 x-2x】x,2“ k=1 k=1 x B 的分布函数F(x)对于任意x满足 ∑X-4 lim F (x)=lim P k= ≤X n-→o B e2dt=Φ(x)

则随机变量之和的标准化变量                     n k k n k k n k k n D X X E X Z 1 1 1 n n k k n k k B X      1 1  的分布函数 Fn (x) 对于任意 x满足                        x B X F x P n n k k n k k n n n 1 1 lim ( ) lim      x t e dt (x). 2π 1 2 2 

概率论与敖理统计 定理五表明： 无论各个随机变量X1,X2,.,Xm,.服从什么 分布，只要满足定理的条件，那么它们的和∑X。 k 当n很大时，近似地服从正态分布

定理五表明: , . , , , , , , 1 1 2 当 很大时 近似地服从正态分布 分布 只要满足定理的条件 那么它们的和 无论各个随机变量 服从什么 n X X X X n k k n   

概率论与数理统外 定理六（德莫佛一拉普拉斯定理） 设随机变量nn(n=1,2,)服从参数为n,p (0<p<1)的二项分布，则对于任意x,恒有 P{-小2w=om 定理六表明： 正态分布是二项分布的极限分布，当n充分大 时，可以利用该定理来计算二项分布的概率

                 x t n n n x t x np p np P p x n n p e d ( ). 2π 1 (1 ) lim (0 1) , , ( 1,2, ) , 2 2    的二项分布 则 对于任意 恒有 设随机变量  服从参数为 定理六(德莫佛－拉普拉斯定理) 定理六表明: 正态分布是二项分布的极限分布, 当n充分大 时, 可以利用该定理来计算二项分布的概率

概率论与散理统计 例2一船舶在某海区航行，已知每遭受一次海浪 的冲击，纵摇角大于3°的概率为13，若船舶遭受 了90000次波浪冲击，问其中有29500~30500次 角大于3°的概率是多少？

一船舶在某海区航行, 已知每遭受一次海浪 的冲击, 纵摇角大于 3º的概率为1/3, 若船舶遭受 了90 000次波浪冲击, 问其中有29 500～30 500次 角大于 3º的概率是多少？ 例2

概率轮与数理统计 例3参加家长会的人数是一个随机变量X, 且一个学生无家长，1名家长，2名家长参会的情况 分别占0.05,0.8,0.15. 共有学生400人，各家长参会情况相互独立，且服 从同一分布. 1、参会家长数超过450人的概率； 2、有一名家长来参会的学生数不多于340的概率

例3 参加家长会的人数是一个随机变量X， 且一个学生无家长，1名家长，2名家长参会的情况 分别占0.05, 0.8, 0.15. 共有学生400人，各家长参会情况相互独立，且服 从同一分布. 1、参会家长数超过450人的概率； 2、有一名家长来参会的学生数不多于340的概率