《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第四章 随机变量的数字特征 第三节 协方差及相关系数

概率论与散理统计 第三节 协方差及相关系数 一、协方差的概念及性质 二、相关系数的概念及意义
一、协方差的概念及性质 二、相关系数的概念及意义 第三节 协方差及相关系数

概率论与散理统外「 一、协方差的概念及性质 1.问题的提出 D(X+Y)=D(X)+D(Y)+2E[X-E(X)]Y-E(Y) 若随机变量X和Y相互独立,那么 D(X+Y)=D(X)+D(Y)
1. 问题的提出 若随机变量 X 和Y 相互独立,那么 D(X Y ) D(X) D(Y ). D X Y D X D Y E X E X Y E Y ( ) ( ) ( ) 2 {[ ( )][ ( )]}. 一、协方差的概念及性质

概率论与敖理统计 2.协方差(Covariance)的定义 量E{[X-E(X)IY-E(Y)}称为随机变量 X与Y的协方差.记为Cov(X,Y),即 Cov(X,Y)=EX-E(X)]Y-E(Y)] 3.协方差的计算公式 Cov(X,Y)=E(XY)-E(X)E(Y)
Cov( , ) {[ ( )][ ( )]}. . Cov( , ), {[ ( )][ ( )]} X Y E X E X Y E Y X Y X Y E X E X Y E Y 与 的协方差 记为 即 量 称为随机变量 2. 协方差( Covariance )的定义 3. 协方差的计算公式 Cov( X,Y) E(XY) E(X )E(Y)

概率伦与散理统针」 4.性质 Cov(X,Y)=E(XY)-E(X)E(Y) (1)Cov(X,Y)=Cov(Y,X); (2)Cov(X,bY)=bCov(X,Y),a,b为常数; (3)Cov(Xi+X2,Y)=Cov(X1,Y)+Cov(X2,Y)
4. 性质 (1) Cov(X,Y ) Cov(Y, X); (2) Cov(aX,bY ) abCov(X,Y ), a, b 为常数; (3) Cov( , ) Cov( , ) Cov( , ). X1 X2 Y X1 Y X2 Y Cov( X ,Y ) E( X Y ) E( X )E(Y )
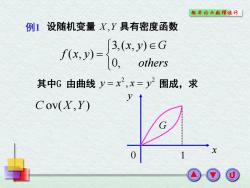
概率论与敖理统外 例1设随机变量X,Y具有密度函数 .)-(EG 0, others 其中G由曲线y=x2,x=y2围成,求 y Cov(X,Y)
例1 设随机变量 X Y, 具有密度函数 3,( , ) ( , ) 0, x y G f x y others 其中G 由曲线 2 2 y x x y , 围成,求 C X Y ov( , ) y x 0 1 G

概率论与散理统外 说明 ()若随机变量X和Y相互独立,则 Cov(X,Y)=0 (2)一般地, D(X±Y)=D(X)+D(Y) ±2CoV(X,Y)
Cov( X ,Y) 0 (1) 若随机变量 X 和Y 相互独立,则 说明 (2) 一般地, D X Y ( ) ( ) ( ) 2 ov( , ) D X D Y C X Y

概率论与敖理统计 二、相关系数的概念及意义 1、定义 Cov(Y,Y) Pw=VDX·DT (D(X)>0,DY)>0) 称为随机变量X与Y的相关系数 2、计算公式 E(XY)-E(X)E(Y) Px灯= VD(X)·VD(Y)
二、 相关系数的概念及意义 . ( ( ) 0 ( ) 0) ( ) ( ) Cov( , ) 称为随机变量 X 与Y 的相关系数 D X ,D Y D X D Y X Y ρXY 1、定义 2、计算公式 ( ) ( ) ( ) ( ) ( ) D X D Y E XY E X E Y ρXY

概率论与散理统外「 3、相关系数的意义 问a,b应如何选择,可使a+bX最接近Y? 接近的程度又应如何来衡量? 设e=E(Y-(a+bX)2] 均方误差 则e可用来衡量a+bX近似表达Y的好坏程度. 当e的值越小,表示a+bX与Y的近似程度越好. 确定a,b的值,使e达到最小
3、相关系数的意义 ? , , ? 接近的程度又应如何来衡量 问a b 应如何选择 可使 a bX 最接近 Y [( ( )) ] 2 设 e E Y a bX 则 e 可用来衡量 a bX 近似表达 Y 的好坏程度. 当 e的值越小,表示 a bX 与Y 的近似程度越好. 确定 a,b的值,使 e 达到最小. 均方误差

概率论与散理统计 e=E[(Y-(a+bX)2] =E(Y2)+b2E(X2)+a2-2bE(XY)+2abE(X) -2aE(Y). 将e分别关于a,b求偏导数,并令它们等于零,得 e=2a+2bE(X)-2EY)=0, O be =2bE(X2)-2E(XY)+2aE(X)=0. 解得A=X,”a=E)-E(X),” D(X) D(X)
2 ( ). ( ) ( ) 2 ( ) 2 ( ) 2 2 2 2 aE Y E Y b E X a bE XY abE X 将 e 分别关于 a,b 求偏导数,并令它们等于零,得 2 ( ) 2 ( ) 2 ( ) 0. 2 2 ( ) 2 ( ) 0, 2 bE X E XY aE X b e a bE X E Y a e 解得 , ( ) Cov( , ) 0 D X X Y b . ( ) Cov( , ) ( ) ( ) 0 D X X Y a E Y E X [( ( )) ] 2 e E Y a bX

概率论与数理统外」 将a,b代入e=E[(Y-(a+bX)2]中,得 mine E[(Y-(a+bx))2] a,b E[(Y-(ao+bX))2] =(1-py)D(Y):
将 a0 ,b0 代入 e E[(Y (a bX))2 ]中,得 min [( ( )) ] 2 , e E Y a bX a b (1 ) ( ). 2 ρXY D Y [( ( )) ] 2 E Y a0 b0X
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第四章 随机变量的数字特征 第四节 矩、协方差矩阵.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第三章 多维随机变量及其分布 第一节 二维随机变量.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第三章 多维随机变量及其分布 第二节 边缘分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第三章 多维随机变量及其分布 第三节 条件分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第三章 多维随机变量及其分布 第四节 相互独立的随机变量.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第三章 多维随机变量及其分布 第五节 两个随机变量的函数的分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第二章 随机变量及其分布 第一节.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第二章 随机变量及其分布 第二节 离散型随机变量及其分布律.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第二章 随机变量及其分布 第三节 随机变量的分布函数.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第二章 随机变量及其分布 第四节 连续型随机变量及其概率密度.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第二章 随机变量及其分布 第五节 随机变量的函数的分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第一章 概率论的基本概念 第一节 随机试验.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第一章 概率论的基本概念 第二节 样本空间、随机事件.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第一章 概率论的基本概念 第三节 频率与概率.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第一章 概率论的基本概念 第四节 等可能概型(古典概型).pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第一章 概率论的基本概念 第五节 条件概率.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第一章 概率论的基本概念 第六节 独立性.pdf
- 《高等数学》课程教学资源(PPT课件)高等数学1.1 函数与极限.ppt
- 《高等数学》课程教学资源(PPT课件)高等数学1.2 数列的极限.ppt
- 《高等数学》课程教学资源(课件讲稿)高等数学1.3.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第四章 随机变量的数字特征 第二节 方差.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第四章 随机变量的数字特征 第一节 数学期望.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第五章 第二节 中心极限定理.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第五章 第一节 大数定律.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第六章 样本及抽样分布(第二部分).pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第六章 样本及抽样分布(第一部分).pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第七章 参数估计 第七节 单侧置信区间.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第七章 参数估计 第五节 正态总体均值与方差的区间估计.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第七章 参数估计 第四节 区间估计.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第七章 参数估计 第三节 估计量的评选标准.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第七章 参数估计 第一节 点估计.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第八章 假设检验 第三节 正态总体方差的假设检验.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第八章 假设检验 第二节 正态总体均值的假设检验.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第八章 假设检验 第一节 假设检验.pdf
- 《概率论与数理统计》课程教学资源(PPT课件讲稿)第八章 假设检验.ppt
- 《概率论与数理统计》课程教学资源(PPT课件讲稿)第七章 参数估计.ppt
- 《概率论与数理统计》课程教学资源(PPT课件讲稿)第六章 样本及抽样分布.pdf
- 《概率论与数理统计》课程教学资源(PPT课件讲稿)第五章 大数定律和中心极限定理.pdf
- 《概率论与数理统计》课程教学资源(PPT课件讲稿)第四章 随机变量的数字特征.pdf
- 《概率论与数理统计》课程教学资源(PPT课件讲稿)第三章 多维随机变量及其分布.ppt
