《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第二章 随机变量及其分布 第四节 连续型随机变量及其概率密度

概率论与数理统外「 第四节连续型随机变量 及其概率密度 一、概率密度的概念与性质 二、常见连续型随机变量
一、概率密度的概念与性质 二、常见连续型随机变量 第四节 连续型随机变量 及其概率密度

概率论与敖理统外 一、概率密度的概念与性质 1.定义 对于随机变量X的分布函数 F(x), 如果存在非负函数∫(x),对于任意实数x有 F(x)=」广nf)dt, 则称X为连续型随机变量, ∫(x)为X的概率密度函数,简称概率密度
一、概率密度的概念与性质 ( ) ( ) d , x F x f t t X f x( ), 1.定义 对于随机变量 的分布函数 如果存在非负函数 F x( ), 对于任意实数 x 有 则称 X 为连续型随机变量, f x( ) 为 X 的概率密度函数,简称概率密度
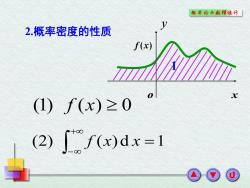
概率论与散理统外「 2.概率密度的性质 f(x) (1)f(x)≥0 (2)f(x)dx=1
2.概率密度的性质 o x f (x) 1 (1) f (x) 0 (2) ( )d 1 f x x y

概率论与敖理统计 f(x)1 X x2 (3)P{x<X≤2}=F(x2)-F(x) =J"f(x)dx
o x f (x) 1 S1 x1 x2 1 2 2 1 3 { } ( ) ( ) P x X x F x F x 2 1 ( )d x x f x x

概率论与数理统针「 注1 I)PX≤=F四=∫fx)dx, (2)P{X>a=1-P{X≤=1-F(a) =∫f(x)dx. (3)在)的连续点处F'(x)=∫(x)
P{X a} F(a) f (x)d x, a P{X a} 1 P{X a} 1 F(a) f (x)d x. a 注1 (1) (2) (3)在 f(x) 的连续点处 F x f x ( ) ( )

概率论与散理统计 注2 对于任意实数值α,连续型随机变量取α的概 率等于零.即P{X=}=0. P{a≤X≤b}=P{a<X≤b=P{a≤X<b} =P{a<X<b}. PX=a}=0,{X=a}并非不可能事件
对于任意实数值 a ,连续型随机变量取 a 的概 率等于零.即 P{X a} 0. P{a X b} P{a X b} P{a X b} P{a X b}. 注2 P X a { } 0, { X= a }并非不可能事件

概率论与散理统外「 例1设随机变量X具有概率密度 kx, 0≤x<3, f(x)=2- 2 3≤x≤4, 0, 其它 (1)确定常数k; (2)求X的分布函数; 3)求P1<X≤2》
}. 2 7 (3) {1 (1) ; (2) ; 0, . , 3 4, 2 2 , 0 3, ( ) P X k X x x kx x f x X 求 确定常数 求 的分布函数 其它 例1 设随机变量 具有概率密度

概率论与敖理统计 例2 设连续型随机变量X的分布函数为 0, x≤-0, F(x)=A+Barcsin,-a. 求:(I)系数A,B的值; 2)P-a<X<: (3)随机变量X的概率密度
(3) . }; 2 (2) { : (1) , ; 1, . arcsin , , 0, , ( ) 随机变量 的概率密度 求 系数 的值 设连续型随机变量 的分布函数为 X a P a X A B x a a x a a x A B x a F x X 例2

概率论与散理统外「 0, x≤-a, 11 所以F(x)= 2+元arcsin -aa
1, . arcsin , , 1 2 1 0, , ( ) x a a x a a x x a 所以 F x

概率论与散理统计 二、常见连续型随机变量的分布 1.均匀分布 定义设连续型随机变量X具有概率密度 a<x<b, 0,其它 则称X在区间(4,b)上服从均匀分布 f(x) 记作X~U(4,b) a o b
二、常见连续型随机变量的分布 1. 均匀分布 x o f (x) a b 定义 设连续型随机变量X 具有概率密度 则称 X 在区间(a, b)上服从均匀分布 1 , , ( ) 0, , a x b f x b a 其它 记作 X~ U(a, b)
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第二章 随机变量及其分布 第五节 随机变量的函数的分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第一章 概率论的基本概念 第一节 随机试验.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第一章 概率论的基本概念 第二节 样本空间、随机事件.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第一章 概率论的基本概念 第三节 频率与概率.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第一章 概率论的基本概念 第四节 等可能概型(古典概型).pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第一章 概率论的基本概念 第五节 条件概率.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第一章 概率论的基本概念 第六节 独立性.pdf
- 《高等数学》课程教学资源(PPT课件)高等数学1.1 函数与极限.ppt
- 《高等数学》课程教学资源(PPT课件)高等数学1.2 数列的极限.ppt
- 《高等数学》课程教学资源(课件讲稿)高等数学1.3.pdf
- 《高等数学》课程教学资源(PPT课件)高等数学1.4 无穷小与无穷大.ppt
- 《高等数学》课程教学资源(PPT课件)高等数学1.5 极限运算法则.ppt
- 《高等数学》课程教学资源(PPT课件)高等数学1.6 极限存在准则及两个重要极限.ppt
- 《高等数学》课程教学资源(课件讲稿)高等数学1.7.pdf
- 《高等数学》课程教学资源(课件讲稿)高等数学1.8.pdf
- 《高等数学》课程教学资源(课件讲稿)高等数学1.9.pdf
- 《高等数学》课程教学资源(PPT课件)高等数学1.10 闭区间上连续函数的性质.ppt
- 《高等数学》课程教学资源(课件讲稿)高等数学2.1.pdf
- 《高等数学》课程教学资源(PPT课件)高等数学2.2 函数的求导法则.ppt
- 《高等数学》课程教学资源(PPT课件)高等数学2.3 高阶导数.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第二章 随机变量及其分布 第三节 随机变量的分布函数.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第二章 随机变量及其分布 第二节 离散型随机变量及其分布律.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第二章 随机变量及其分布 第一节.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第三章 多维随机变量及其分布 第五节 两个随机变量的函数的分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第三章 多维随机变量及其分布 第四节 相互独立的随机变量.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第三章 多维随机变量及其分布 第三节 条件分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第三章 多维随机变量及其分布 第二节 边缘分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第三章 多维随机变量及其分布 第一节 二维随机变量.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第四章 随机变量的数字特征 第四节 矩、协方差矩阵.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第四章 随机变量的数字特征 第三节 协方差及相关系数.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第四章 随机变量的数字特征 第二节 方差.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第四章 随机变量的数字特征 第一节 数学期望.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第五章 第二节 中心极限定理.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第五章 第一节 大数定律.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第六章 样本及抽样分布(第二部分).pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第六章 样本及抽样分布(第一部分).pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第七章 参数估计 第七节 单侧置信区间.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第七章 参数估计 第五节 正态总体均值与方差的区间估计.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第七章 参数估计 第四节 区间估计.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿,48学时)第七章 参数估计 第三节 估计量的评选标准.pdf
