《高等数学》课程教学资源（PPT课件）高等数学4.1 不定积分

第四章 不定积分 微分法：F'(x)=(?) 互逆运算 积分法：(？)=f(x)

第四章 微分法: F(x) = ( ? ) 积分法: ( ? ) = f (x) 互逆运算 不定积分

第一节 第四章 不定积分的概念与性质 一、 原函数与不定积分的概念 二、 基本积分表 三、不定积分的性质 HIGH EDUCATION PRESS 机动目录上页下页返回结束

二、 基本积分表 三、不定积分的性质 一、 原函数与不定积分的概念 第一节 机动 目录 上页 下页 返回 结束 不定积分的概念与性质 第四章

一、原函数与不定积分的概念 引例：一个质量为m的质点，在变力F=Asint的作 下沿直线运动，试求质点的运动速度v(t) 、FA 根据牛顿第二定律，加速度a(d)= =-sint mm 因此问题转化为已知0=1sn1,求0=？ m 定义1.若在区间I上定义的两个函数F(x)及f(x) 满足F'(x)=f(x)或dF(x)=f(x)d,则称F(x)为f(x) 在区间1上的一个原函数 HIGH EDUCATION PRESS 机动目录上页下页返回结束

一、 原函数与不定积分的概念 引例: 一个质量为 m 的质点, 下沿直线运动 , 因此问题转化为: 已知 ( ) sin t , m A v  t = 求 v(t) = ? 在变力 试求质点的运动速度 机动 目录 上页 下页 返回 结束 根据牛顿第二定律, 加速度 定义 1 . 若在区间 I 上定义的两个函数 F (x) 及 f (x) 满足 在区间 I 上的一个原函数 . 则称 F (x) 为f (x)

问题： 1.在什么条件下，一个函数的原函数存在？ 2.若原函数存在，它如何表示？ 定理1.若函数f(x)在区间1上连续，则f(x)在I上 存在原函数 初等函数在定义区间上连续 初等函数在定义区间上有原函数 HIGH EDUCATION PRESS 机动目录上页下页返回结束

问题: 1. 在什么条件下, 一个函数的原函数存在 ? 2. 若原函数存在, 它如何表示 ? 定理1. 存在原函数 . 初等函数在定义区间上连续 初等函数在定义区间上有原函数 机动 目录 上页 下页 返回 结束

说明：若F(x)是f(x)的一个原函数，则f(x)的所有 原函数都在函数族F(x)+C(C为任意常数)内 证：1)(F(x)+C)'=F'(x)=f(x) ∴F(x)+C是f(x)的原函数 2)设Φ(x)是f(x)的任一原函数，即 Φ'(x)=f(x) 又知 F'(x)=f(x) .[Φ(x)-F(x)]=Φ'(x)-F'(x)=f(x)-f(x)=0 故 D(x)=F(x)+C。(Co为某个常数) 即①(x)=F(x)+C,属于函数族F(x)+C. HIGH EDUCATION PRESS 0◆0C08 机动目录上页下页返回结束

说明： 原函数都在函数族 ( C 为任意常数 ) 内 . 证: 1) 又知  [(x) − F(x)] = (x) − F(x) = f (x) − f (x) = 0 故 0 (x) = F(x) +C ( ) C0为某个常数 即 0 (x) = F(x) +C 属于函数族 F(x) +C . 机动 目录 上页 下页 返回 结束 即

定义2.f(x)在区间I上的原函数全体称为f(x)在 上的不定积分，记作f(x)dx,其中 ∫- 积分号； f(x)一被积函数； 积分变量；f(x)dx一被积表达式. 若F'(x)=f(x),则 「f(x)dr=F(x)+C(C为任意常数) 例如， [e"dx=ex+C C称为积分常数 「x2dx=x3+C 不可丢！ sin xdx -cos x+C HIGH EDUCATION PRESS 动目录上页下页返回结束

定义 2. 在区间 I 上的原函数全体称为 上的不定积分, 其中 — 积分号; — 被积函数; — 积分变量; — 被积表达式. 若 则 ( C 为任意常数 ) C 称为积分常数 不可丢 ! 例如, =  e x x d e C x + =  x dx 2 x +C 3 3 1 =  sin xdx − cos x +C 记作 机动 目录 上页 下页 返回 结束

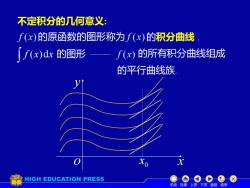
不定积分的几何意义： ∫(x)的原函数的图形称为f(x)的积分曲线 ∫x)d的图形 一f(x)的所有积分曲线组成 的平行曲线族 Xo HIGH EDUCATION PRESS e0C8 机动目录上页下页返回结束

不定积分的几何意义: 的原函数的图形称为 f (x)dx  的图形 的所有积分曲线组成 的平行曲线族. y o x0 x 机动 目录 上页 下页 返回 结束 的积分曲线

例3.设曲线通过点(1,2)，且其上任一点处的切线 斜率等于该点横坐标的两倍，求此曲线的方程 解：y=2x y=∫2xdr=x2+C 所求曲线过点(1,2)，故有 1,2) 2=12+C .C=1 因此所求曲线为y=x2+1 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例3. 设曲线通过点( 1 , 2 ) , 且其上任一点处的切线 斜率等于该点横坐标的两倍, 求此曲线的方程. 解: 所求曲线过点 ( 1 , 2 ) , 故有 因此所求曲线为 1 2 y = x + 机动 目录 上页 下页 返回 结束 y o x (1, 2)

从不定积分定义可知 Ij/r]-f)或djrd]=fd (2) jFx)d=F)+C或∫aF)=FC 二、 基本积分表P188) 利用逆向思维 () 「kdx=Kx+C (k为常数) (2) ∫xdx=4x+C (4≠-1) )=nx+C x<0时 (lnx)y'=[ln(-x)]'= HIGH EDUCATION PRESS 机动目录上页下页返回结束

 d x d (1)  f (x)d x  = f (x) 二、 基本积分表 (P188) 从不定积分定义可知: d   或 f (x)dx  = f (x)dx x = +C  (2) F(x) d F(x) 或 = +C  d F(x) F(x) 利用逆向思维 =  (1) kdx kx +C ( k 为常数) =  (2) x dx  x +C + + 1 1 1   =  x d x (3) ln x +C x  0时 机动 目录 上页 下页 返回 结束 (  −1) (ln x ) = [ln(−x)] x 1 =

4) arctan x+C 或 -arccot x+C I+x dx (⑤) arcsinx+C或 ;arccos x+C 1-x (6) cos xdx sinx+C (7) sin xdx =-cosx+C (8) 9) HIGH EDUCATION PRESS 机动目录上页下页返回结束

= +  2 1 d (4) x x arctan x +C =  (6) cos xdx sin x +C =  x x 2 cos d (8) =  sec xdx 2 tan x +C 或 − arccot x +C = −  2 1 d (5) x x arcsin x +C 或 − arccos x +C =  (7) sin xdx − cos x +C =  x x 2 sin d (9) =  csc xdx 2 − cot x +C 机动 目录 上页 下页 返回 结束