《高等数学》课程教学资源（PPT课件）高等数学6.2 定积分在几何学上的应用

第二节 第六章 定积分在儿何学上的立用 平面图形的面积 二、平面曲线的弧长 三、 已知平行截面面积函数的 立体体积 HIGH EDUCATION PRESS 机动目录上页下页返回结束

三、已知平行截面面积函数的 立体体积 第二节 一、 平面图形的面积 二、 平面曲线的弧长 机动 目录 上页 下页 返回 结束 定积分在几何学上的应用 第六章

一、平面图形的面积 1.直角坐标情形 y↑y=f(x 设曲线y=f(x)(20)与直线 x=a,x=b(a<b)及x轴所围曲 边梯形面积为A,则 o a x\,b x+dx dA=f(x)dx 4-G)dx y=(x)y=f2(x) 右下图所示图形面积为 4=[F(x)-S(x)dx axx+dx HIGH EDUCATION PRESS 机动目录上页下页返回结束

一、平面图形的面积 1. 直角坐标情形 设曲线 与直线 及 x 轴所围曲 则 dA = f (x)dx o a b x y y = f (x) x x + dx A f x x b a ( )d  = 机动 目录 上页 下页 返回 结束 边梯形面积为 A , 右下图所示图形面积为 y o a b x ( ) 2 ( ) y = f x 1 y = f x A f x f x x b a ( ) ( ) d =  1 − 2 x x + d x

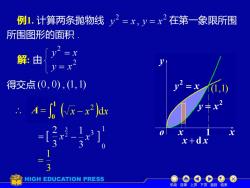
例1.计算两条抛物线y2=x,y=x2在第一象限所围 所围图形的面积 解：由 y-=x y=x 得交点(0,0)，1,1) A=0(x-x2 -5- x+dx HIGH EDUCATION PRESS 机动目录上页下页返回结束

例1. 计算两条抛物线 在第一象限所围 所围图形的面积 . x y = x 2 o y 2 y = x x x + d x 解: 由 得交点 (0, 0) , (1,1) (1,1) 1 d A ( x x )dx 2 = − 3 1 =   = 1 0 A 机动 目录 上页 下页 返回 结束

例2.计算抛物线y2=2x与直线y=x-4所围图形 的面积 解：由 y2=2x 得交点 y=x-4 1y2=2x 7(8,4) V+d (2,-2),(8,4) 为简便计算，选取y作积分变量， 则有 A=2(y+4-2)d =[2y2+4y-y3]12=18 HIGH EDUCATION PRESS 机动目录上页下页返回结束

x y 2x 2 = o y y = x − 4 例2. 计算抛物线 y 2x 2 = 与直线 的面积 . 解: 由 得交点 (2, − 2) , (8, 4) (8,4) d A ( y 4 y )dy 2 2 1 = + − =18 y = x − 4 所围图形 (2,− 2) 为简便计算, 选取 y 作积分变量, 则有 y y + d y −  = 4 2 A 机动 目录 上页 下页 返回 结束

例3.求椭圆 =1所围图形的面积 62 解：利用对称性，有dA=ydx =4a 利用椭圆的参数方程 oxx+dxa x x =acost y=bsint (0≤t≤2π) 应用定积分换元法得 1=4 bsint.(-asint)dt 4ab sin2tdt -4ab =πab 当a=b时得圆面积公式 HIGH EDUCATION PRESS 色0C⊙8 机动目录上页下页返回结束

a b o x y x 例3. 求椭圆 解: 利用对称性 , d A = y dx 所围图形的面积 . 有  = a A y x 0 4 d 利用椭圆的参数方程 (0 2 ) sin cos       = = t y b t x a t 应用定积分换元法得  = 2 0 2 4 sin d  ab t t = 4ab 2 1  2   =  ab 当 a = b 时得圆面积公式 机动 目录 上页 下页 返回 结束 x + d x

2.极坐标情形 设p(0)eC[a,B],p(0)≥0，求由曲线r=p(0)及 射线0=α，0=B围成的曲边扇形的面积 在区间a,B]上任取小区间[0,0+d0] 则对应该小区间上曲边扇形面积的近似值为 d4=ooj产a0 所求曲边扇形的面积为 A-)d0 HIGH EDUCATION PRESS 机动目录上页下页返回结束

2. 极坐标情形 求由曲线 及 围成的曲边扇形的面积 . r =( )  x  d 在区间 上任取小区间 则对应该小区间上曲边扇形面积的近似值为 ( ) d 2 1 d 2 A = 所求曲边扇形的面积为      ( )d 2 1 2  A = 机动 目录 上页 下页 返回 结束 

例4.计算阿基米德螺线r=a0(a>0)对应0从0变 到2π所围图形面积 24 点击图片任意处 播放开始或暂停 HIGH EDUCATION PRESS ©-◆OC①8 机动目录上页下页返回结束

例4. 计算阿基米德螺线 对应  从 0 变 解: x 2 a o  d (  ) d 2 1 2 a  = 2 0 A 2 2 a =       3 3 1  0 2 3 2 3 4 =  a 点击图片任意处 播放开始或暂停 机动 目录 上页 下页 返回 结束 到 2 所围图形面积

例5.计算心形线r=a1+cos0)(a>0)所围图形的 面积 解4=2心a+eoa论 (利用对称性) 、d8 令1=g -8a2cos*rdr =8a23.1.z3 4222 HIGH EDUCATION PRESS 心形线目录上页下页返回结束

8a cos t dt 2 0 2 4  =  例5. 计算心形线 所围图形的 面积 . 解: o 2a x  d (1 cos ) d 2 1 2 2 a +  =  0 2 a   d 2 4cos4 (利用对称性) 2  令t = =  2 8a  4 3  2 1 2  2 2 3 =  a 心形线 目录 上页 下页 返回 结束

二、已知平行截面面积函数的立体体积 设所给立体垂直于x轴的截面面积为4A(x),A(x)在[a,b] 上连续，则对应于小区间[x,x+dx]的体积元素为 dV=A(x)dx 因此所求立体体积为 V=f(x)dx A(x) xx+dx HIGH EDUCATION PRESS 机动目录上页下页返回结束

二、已知平行截面面积函数的立体体积 设所给立体垂直于x 轴的截面面积为A(x), 则对应于小区间 的体积元素为 dV = A(x)d x 因此所求立体体积为 V A x x b a ( )d  = 机动 目录 上页 下页 返回 结束 a x b x A(x) 上连续

特别，当考虑连续曲线段y=f(x)(a≤x≤b)绕x轴 轴旋转一周围成的立体体积时，有 1 y=f(x) V-[f(Pdx 当考虑连续曲线段 x=p()(c≤y≤d) 绕y轴旋转一周围成的立体体积时， 有 X三 e(r) V=∫πlovd HIGH EDUCATION PRESS 机动目录上页下页返回结束

x y o a b x y o a b y = f (x) 特别 , 当考虑连续曲线段 2  [ f (x)] 轴旋转一周围成的立体体积时, 有 dx  = b a V 当考虑连续曲线段 绕 y 轴旋转一周围成的立体体积时, 有 2  [( y)] dy  = d c V x o x y x =( y) c d y 机动 目录 上页 下页 返回 结束