《电磁场与电磁能》课程PPT教学课件（马冰然版）复习题题

例：求标量场= ln(x2++z2）通过点M（1，2，3）的等值面方程。解：函数在点M（1，2，3）处的值为Φ = ln(x? + y2 +z2) = ln(1? +22 +33) = ln 14故通过点M（1，2，3）的等值面方程In(x2 + y2 +z2)= ln 14即x? + j? +2?=14

例：求标量场 通过 点M（1，2，3）的等值面方程。 ln( ) 2 2 2  = x + y + z 解：函数在点M（1，2，3）处的值为 ln( ) ln(1 2 3 ) ln14 2 2 2 2 2 2  = x + y + z = + + = 故通过点M（1，2，3）的等值面方程 ln( ) ln14 2 2 2 x + y + z = 14 2 2 2 即 x + y + z =

例1-4:求函数u=/x2+2+z2 在点 M(1,0,1)处沿7=a,+2a,+2a方向的方向导数解：au1Oux2axax+2+z2auyu=0M(1,0,1)ayVay1ouauZ-2OzOz

例1-4： 求函数 u = x 2 + y 2 + z 2 在点 M(1,0,1) 处沿 l a 2a 2a 方向的方向导数. x y z     = + + 解： 2 2 2 x y z x x u + + =    2 2 2 x y z y y u + + =   2 2 2 x y z z z u + + =   M(1,0,1) 2 1 =   x u = 0   y u 2 1 =   z u 2 2 2 x y z y y u + + =   2 1 =   x u = 0   y u 2 2 2 x y z y y u + + =   2 1 =   x u 2 1 =   z u = 0   y u 2 2 2 x y z y y u + + =   2 1 =   x u

=a+27-2a而7的方向余弦为Al =aAx+a,Ay+a.Az11COSX32VP+2+2cosB3V12+ 22+ 2222cOS:3/12 + 22 + 22函数u在M点沿7方向的方向导数为：211121Ou+0xV223323al

而 l 的方向余弦为  3 1 1 2 2 1 cos 2 2 2 = + +  = 3 2 1 2 2 2 cos 2 2 2 = + +  = 3 2 1 2 2 2 cos 2 2 2 = + +  = 2 1 3 2 2 1 3 2 0 3 1 2 1 =  +  +  =   l M u 点沿 l 方向的方向导数为：  函数 u 在 M ax ay az l     = + 2 + 2 l a x a y a z  = x  + y  + z      3 1 1 2 2 1 cos 2 2 2 = + +  = 3 2 1 2 2 2 cos 2 2 2 = + +  =

例： 求标量场 u= xy2 +yz3 在点M(2,-1,1)处的梯度,以及在矢量i=2a,+2a,-a.方向的方向导数解:OuOuOugradiOzOxOya,y? +a,(2xy+z3) +a,3yz2M(2,-1,1)VuM=ax-3a,-3a而7的方向余弦为

例： 求标量场 u = x y 2 + yz 3 在点 M(2,−1,1)处 的梯度,以及在矢量 l 2 a 2 a a 方向的方向导数. x y z     = + − 解： zu a yu a xu gradu a x y z  +   +   =     2 3 2 a y a ( 2x y z ) a 3yz x y z    = + + + M ( 2 , − 1 , 1 ) M x y z u a a a     = − 3 − 3 而 l 的方向余弦为 

I = 2a +2a,-a.2-2cosα =3/22 +22 +(-1)222cosB=3/22 +22 +(-1)21--1cOSy3V22 +2? +(-1)2函数u在M点沿1方向的方向导数为2Ou27=1x-3)al lm33

3 2 2 2 ( 1) 2 cos 2 2 2 = + + −  = 3 2 2 2 ( 1) 2 cos 2 2 2 = + + −  = 3 1 2 2 ( 1) 1 cos 2 2 2 = − + + − −  = 点沿 l 方向的方向导数为：  函数 u 在 M 3 1 ) 3 1 ( 3) ( 3 2 ( 3) 3 2 =1 + −  + −  − = −   l M u l 2a 2a a . x y z      = + −

例1-6:： R= 1(x-x')2 +(y-y)? +(z - z)?试证明O其中R=r-r'ZM(x, y,2)M(x,y',z)矢径场点源点!rVx

例1-6： ( ) ( ) ( ) , 2 2 2 R = x − x  + y − y  + z − z  试证明 ) 1 ) ( 1 ( R R  = − z a y a x ax y z    +    +     = 其中    y x o z M (x, y,z) M (x  , y  ,z ) r   r  R = r − r     矢径 源点 场点

V[(x-x)2 +(-y) +(z-z)3j 2证：[(x-x)? +(-y)2 +(z-z)]2P[(x-x) +(-y)2 +(z-z)]2+a[(x-x')2 +(-)2 +(z-z)]2+a静电场5a,(x-x)+a,(y-y)+a.(z-z)[(x-x)2 +(y-y')2 +(z-z)?jRr-rR3<Rr-r

证： 2 1 2 2 2 ) [( ) ( ) ( ) ] 1 ( −  =  x − x  + y − y  + z − z  R 2 1 2 2 2 [( ) ( ) ( ) ] − −  + −  + −    = x x y y z z x ax  2 1 2 2 2 [( ) ( ) ( ) ] − −  + −  + −    + x x y y z z y ay  2 1 2 2 2 [( ) ( ) ( ) ] − −  + −  + −    + x x y y z z z az  2 3 2 2 2 [( ) ( ) ( ) ] ( ) ( ) ( ) x x y y z z a x x a y y a z z x y z −  + −  + −  −  + −  + −  = −    3 3 ) 1 ( r r r r R R R −  −    = − = −      静电场5

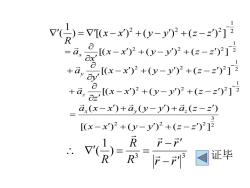
= V[(x-x)? +(y-y')2 +(z-z)j 2R0[(x-x)? +(-y)2 +(z-z)2]2ago[(x-x)? +(-y')2 +(z-z)]2-aX.0[(x-x')2 +(y-y)2 +(z-z)2j2+aaa,(x-x)+a,(y-y)+a,(z-z)[(x-x)? +(y-y')2 +(z-z)j2R-r证毕R3R-

2 1 2 2 2 ) [( ) ( ) ( ) ] 1 ( −  =  x − x  + y − y  + z − z  R 2 1 2 2 2 [( ) ( ) ( ) ] − −  + −  + −     = x x y y z z x ax  2 1 2 2 2 [( ) ( ) ( ) ] − −  + −  + −     + x x y y z z y ay  2 1 2 2 2 [( ) ( ) ( ) ] − −  + −  + −     + x x y y z z z az  2 3 2 2 2 [( ) ( ) ( ) ] ( ) ( ) ( ) x x y y z z a x x a y y a z z x y z −  + −  + −  −  + −  + −  =    3 3 ) 1 ( r r r r R R R −  −    = =      证毕

例1-10:沿着在xo面上的一个闭合路径0@求A=ax?+ay?+a2的线积分。此闭合路径由在（0，0）和（2,V2）之间的一段抛物线y2=两段平行于坐标轴的直线段组成，如图yD所示。②计算A的旋度。解：@A.di=(a,x?+a,y+a.2).(a,dx+a,dy+a.d2)=(a,x? +a,y? +a.z).(adx+a,dy)44= xdx+ y2dyfAdi -f'A.di +f'A.di + ,A.di-(x'dx+ydy)+ (x'dx+yd)+ (x'dx+y'dy)

y 例1-10： ①求 2 2 2 A a x a y a z x y z     = + + 沿着在 面上的一个闭合路径C 的线积分。此闭合路径由在（0，0）和（2， 2 ）之间的一 段抛物线 y = x 2 和两段平行于坐标轴的直线段组成，如图 所示。②计算 A 的旋度。  xoy 解：① ( ) ( ) 2 2 2 A dl a x a y a z a dx a dy a dz x y z x y z          = + +  + + x dx y dy a x a y a z a dx a dy x y z x y 2 2 2 2 2 ( ) ( ) = + = + +  +           =  +  +  O D D B B O C A dl A dl A dl A dl            = + + + + + O D D B B O (x dx y dy) (x dx y dy) (x dx y dy) 2 2 2 2 2 2

在路径O>B上，有 y=0,dy=0,x由0→2;在路径 B→>D上，有 x=2,dx=0,y由0→2:在路径 D→0上，有 x由2→0,y由V2→0;:. $ A.di = [(x’dx+ y'dy)+ [' (x’dx+ y'dy)+ [(x?dx+ y'dy)y?dydy0A的环量等于零

y 在路径 O→B 上，有 y = 0,dy = 0; x由0→2; 在路径 B → D 上，有 x = 2,dx = 0, y由0 → 2; 在路径 D →O 上，有 x由2 → 0, y由 2 → 0;       = + + + + + O D D B B O C A dl (x dx y dy) (x dx y dy) (x dx y dy) 2 2 2 2 2 2       = + + + 0 2 2 0 2 2 2 0 2 2 0 2 x dx y dy x dx y dy 0 3 3 3 3 3 3 3 3 0 2 0 2 2 0 2 0 = + + + = x y x y A 的环量等于零。 