《电磁场与电磁能》课程PPT教学课件（杨儒贵版）第六章 电磁感应

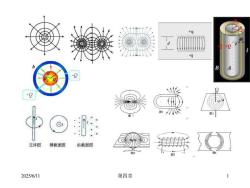
e立体图横截面飘截面图第四章2025/6/11

2025/6/11 第四章 1

第六章电磁感应主要内容电磁感应定律，自感与互感，能量与力。电磁感应定律由物理学知，穿过闭合线圈中的磁通发生变化时，线圈中产生的感应电动势e为d@Φe=dt式中电动势e的正方向规定为与磁通方向构成右旋关系。因此，当磁通增加时，感应电动势的实际方向与磁通方向构成左旋关系；反之，当磁通减少时，电动势的实际方向与磁通方向构成右旋关系

第六章 电磁感应 主 要 内 容 电磁感应定律，自感与互感，能量与力。 1. 电磁感应定律 由物理学知，穿过闭合线圈中的磁 通发生变化时，线圈中产生的感应电 动势 e 为 t e d d = − 式中电动势 e 的正方向规定为与磁通方向构成右旋关系。 因此，当磁通增加时，感应电动势的实际方向与磁通 方向构成左旋关系；反之，当磁通减少时，电动势的实 际方向与磁通方向构成右旋关系

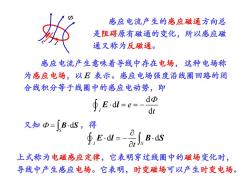
感应电流产生的感应磁通方向总是阻碍原有磁通的变化，所以感应磁通又称为反磁通。感应电流产生意味着导线中存在电场，这种电场称为感应电场，以E表示。感应电场强度沿线圈回路的闭合线积分等于线圈中的感应电动势，即ddd.E.dl=e:dt又知Φ=[B·dS，得df,E.dl =-B.dsOt Js上式称为电磁感应定律，它表明穿过线圈中的磁场变化时，导线中产生感应电场。它表明，时变磁场可以产生时变电场

感应电流产生的感应磁通方向总 是阻碍原有磁通的变化，所以感应磁 通又称为反磁通。 感应电流产生意味着导线中存在电场，这种电场称 为感应电场，以E 表示。感应电场强度沿线圈回路的闭 合线积分等于线圈中的感应电动势，即 d d l d e t   = = −  E l 又知 =   ，得 S  B dS d d l S t   = −     E l B S 上式称为电磁感应定律，它表明穿过线圈中的磁场变化时， 导线中产生感应电场。它表明，时变磁场可以产生时变电场

根据旋度定理，由上式得aBds=0at由于该式对于任一回路面积S均成立，因此，其被积函数一定为零，即aBVxE=at此式为电磁感应定律的微分形式。它表明某点磁通密度时间变化率的负值等于该点时变电场强度的旋度。电磁感应定律是时变电磁场的基本定律之一，也是下一章将要介绍的描述时变电磁场著名的麦克斯韦方程组中方程之一

根据旋度定理，由上式得 ( ) d = 0          +  S B E S t 由于该式对于任一回路面积 S 均成立，因此，其被 积函数一定为零，即 t    = − B E 此式为电磁感应定律的微分形式。它表明某点磁通密度 时间变化率的负值等于该点时变电场强度的旋度。 电磁感应定律是时变电磁场的基本定律之一，也是 下一章将要介绍的描述时变电磁场著名的麦克斯韦方程 组中方程之一

6-2自感与互感在线性介质中，单个闭合回路电流产生的磁通密度与回路电流I成正比，因此穿过回路的磁通也与回路电流I成正比。与回路电流I交链的磁通称为回路电流的磁通链以表示，令与I的比值为L，即y1式中L称为回路的电感，单位为H（亨利）。由该定义可见，电感又可理解为与单位电流交链的磁通链。单个回路的电感仅与回路的形状及尺寸有关，与回路中电流无关。磁通链与磁通不同，磁通链是指与某电流交链的磁通

6-2 自感与互感 在线性介质中， 单个闭合回路电流产生的磁通密度 与回路电流I 成正比，因此穿过回路的磁通也与回路电流 I 成正比。 I L  = 式中L 称为回路的电感，单位为H（亨利）。由该定义可 见，电感又可理解为与单位电流交链的磁通链。 单个回路的电感仅与回路的形状及尺寸有关，与回路 中电流无关。 与回路电流 I 交链的磁通称为回路电流 I 的磁通链， 以 表示，令 与 I 的比值为L，即 磁通链与磁通不同，磁通链是指与某电流交链的磁通

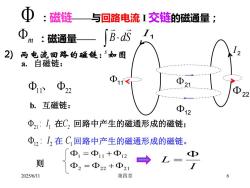
d：磁链与回路电流I交链的磁通量；ΦB.dsm：磁通量2）两电流回路的磁链：“如图a.自磁链：Φ1Φ.Φ.Φud22b.互磁链：Φ12Φ2：I，在C，回路中产生的磁通形成的磁链；Φ，：I,在C回路中产生的磁通形成的磁链Φ, =Φ11 +Φ12则Φ, = Φ22 + Φ211第四章2025/6/11

2025/6/11 第四章 6 2 I 1 I 2) 两电流回路的磁链：如图 a. 自磁链： b. 互磁链： 11 22 12 21 11 22 、 12 : I 2 在 C1 回路中产生的磁通形成的磁链。 21 : I 1 在 C2 回路中产生的磁通形成的磁链； 则 2 22 21 1 11 12  =  +   =  +  I L  =  ：磁链——与回路电流 I 交链的磁通量； m ：磁通量——   s B dS  

若交链N次，则磁通链增加N倍；若部分交链，则必须给予适当的折扣。因此，与N匝回路电流I交链的磁通链为Y=NΦ。那么，由N匝回路组成的线圈的电感为YN@L11Z112I112与回路电流I交链的磁通链dl-rdl是由两部分磁通形成的，其一是F2I本身产生的磁通形成的磁通链，另一是电流I在回路l中产生的磁通形成的磁通链Y12。甲=+f12那么，与电流l交链的磁通链出为

若交链 N 次，则磁通链增加N 倍；若部分交链，则必 须给予适当的折扣。因此，与N 匝回路电流 I 交链的磁通 链为  = N 。那么，由N 匝回路组成的线圈的电感为 I N I L   = = 与回路电流I 1交链的磁通链 是由两部分磁通形成的，其一是 I 1本身产生的磁通形成的磁通链 11 ，另一是电流 I 2 在回路 l 1 中产生的磁通形成的磁通链 12 。 dl1 O z y x dl2 l2 l1 I2 I1 r2 - r1 r2 r1 那么，与电流 l 1 交链的磁通链1为 1 =11 +12

同理，与回路电流I，交链的磁通链为Y, = 421 + Y22Y12.Yi.2及"2均为常数。在线性介质中，比值1’1’I12Y1l12M/I112式中L，称为回路l的自感，1M称为回路l,对l的互感。422P21M.L22同理定义I2I式中L称为回路l,的自感，M称为回路l对l的互感

同理，与回路电流I 2 交链的磁通链为 2 =21 +22 在线性介质中，比值 ， ， 及 均为常数。 1 11 I  2 12 I  2 22 I  1 21 I  式中L11称为回路 l 1的自感，M12称为回路 l 2对 l 1的互感。 同理定义 2 22 22 I L  = 1 21 21 I M  = 式中L22 称为回路 l 2的自感，M21称为回路 l 1对 l 2的互感。 1 11 11 I L  = 2 12 12 I M  令 =

Y = Y1 +412Y, = Y21 +Y22将L1，L22，Mi2及M21代入上两式，得Y= Li/I + M12/2Y, = M21l, + L2212可以证明，在线性均匀介质中M12 = M21因为可以导出任意两个回路之间的互感公式为dl, ·dl,dl, dl,μ6.$$M,M,4元92912-rl4元12-2考虑到dl,·dl,=dl, dl，[z-n=i-r，所以由上两式可见，M12 = M21

将L11，L22，M12 及 M21 代入上两式，得 1 11 1 12 2  = L I + M I 2 21 1 22 2  = M I + L I 可以证明，在线性均匀介质中 M12 = M21 因为可以导出任意两个回路之间的互感公式为 2 1 1 2 21 2 1 d d 4π l l M   = −   l l r r 1 2 2 1 12 1 2 d d 4π l l M   = −   l l r r 考虑到 ，所以由上两式 可见， 1 2 2 1 2 1 1 2 dl dl = dl dl , r −r = r −r M12 = M21 1 =11 +12 2 =21 +22

dl, -dl.dl, -dlM,== duM,24元921-4元J1r-r若dl与dl,处处保持垂直，则互感Mz=M2,=0。若处处保持平行，则互感M值达到最大。因此，在电子电路中，若要增强两个线圈之间的耦合，应彼此平行放置；若要避免两个线圈相互耦合，则应相互垂直。互感可正可负，其值正负取决于两个线圈的电流方向，但电感始终应为正值。若互磁通与原磁通方向相同时，则使磁通链增加，互感应为正值；反之，若互磁通与原磁通方向相反时，则使磁通链减少，互感为负值

2 1 1 2 21 2 1 d d 4π l l M   = −   l l r r 1 2 2 1 12 1 2 d d 4π l l M   = −   l l r r 若 dl1与 dl2 处处保持垂直，则互感 M12 = M21 = 0 。 因此，在电子电路中，若要增强两个线圈之间的耦合， 应彼此平行放置；若要避免两个线圈相互耦合，则应相互 垂直。 互感可正可负，其值正负取决于两个线圈的电流方向， 但电感始终应为正值。 若处处保持平行，则互感M 值达到最大。 若互磁通与原磁通方向相同时，则使磁通链增加，互 感应为正值；反之，若互磁通与原磁通方向相反时，则使 磁通链减少，互感为负值