《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第二章 静电场

AAaA-矢量1.场标量场矢量场静态场时变场AAA-aA+aA,+a.A柱坐标球dl r = drdl = drdl。= rdodl。= rd β长度元dl =rsifdpdl= dz面积元为:dS, = dl,dl, =rdpdz( ds, = dledl。= r? sirdedpdS , = dydzdS。= dl,dl,= r sirodrdp dS. =dldl, =drdz2dS , = dxdzI dS, =dl,dl。 =rdrdoLdS =d,dl, =rdrdbdS, = dxdy体积元dV= dl,dl,dl, =r? sindrddpdv=dxdydz dv=dl,dl,dl,=rdrdpdz
1.场 标量场 矢量场 静态场 时变场 矢量 A A A A A a 面积元为: dS dxdy z dS dydz x dS dxdz y 体积元 dV dxdydz dS dl dl rd dz r z dS dldl drdz r z dSz dl rdl rdrd dV dl dl dl rdrd dz r z dS dl rdl rdrd dS r dl dl r sindd 2 dS dl rdl r sindrd dV dl rdldl r sindrdd 2 dl rsind dl dr r dl rd 球 dl dz z dl dr r dl rd 柱坐标 长度元 x x y y zAz A a A a A a
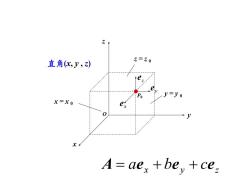
Z=ZO直角(x,y,z)Vx=xoA= aex+be, +ce
直角(x, y , z) z x y z = z 0 x = x 0 P0 y = y 0 z e x e y e O x y z A ae be ce
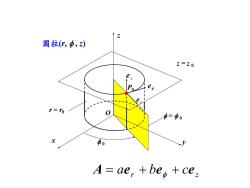
7圆柱(r, Φ,z)Z=Z0e.P10ddoA= aer +be +ce
圆柱(r, , z) y z x P0 0 = 0 r = r0 z = z 0 r e z e e O r z A ae be ce
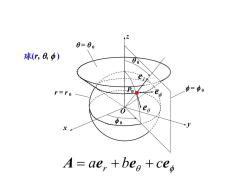
0= 00球(r, e, Φ)=ΦoPr=roeoΦoA=aer +bee +ceg
x z y = 0 0 0 球(r, , ) r = r 0 = 0 e r e e P0 O A ae be ce r

1.矢量加法和减法:A+B=a(A +B,)+a,(A,+B,)+a.(A, +B.)A·B=A|Bcos(A,B)2.点积(或标量积)A· B-AxBx+AyBy+AzBz3.叉积(或矢量积)AxB=ABsin(A,B)axayaAxB=AxAy A.BxByB.=(A,B, -A,B,)ax +(A,Bx-A,B,)a+(A,B,-A,B)a
1.矢量加法和减法: A B ax(Ax Bx ) ay(Ay By ) az(Az Bz ) 2.点积(或标量积) AB A B cos(A,B) A·B=AxBx+AyBy+AzBz 3.叉积(或矢量积) AB A B sin(A,B) y z z y x z x x z y x y y x z x y z x y z x y z A B A B a A B A B a A B A B a B B B A A A a a a ( ) ( ) ( ) AB

Ouu(M)-u(Mo)lim1.方向导数的定义:△1ailMoN/->0QuQuQuOucosβcos αcOS alaxyOzQuQuQu2.梯度的定义:gradu = G= ax.ata-axryayOzuG.△Ilim=G·a/ =|G|cos(G,al)alN△/>0aaaV=aa梯度也可记作a+VuayOzOx
1.方向导数的定义: 0 ( ) ( ) lim 0 0 M l l u l u M u M cos cos cos z u y u x u l u 2.梯度的定义: z u y u x u u x y z grad G a a a lim cos( , ) 0 l l l l l u G a G G a G l x y z a a a x y z 梯度也可记作 u

aaa矢量微分算子Vu=aaa2+axzayQuQuQugraduaaOoxayOzauQuu1柱坐标系中故gradu =u=a-aa一Orrapz11 QuOuOugradu= Vu=a,+a球坐标系aer0Orrsimp
矢量微分算子 ( ) x y z x y z u a a a u x y z u u u a a a gradu x y z z u a u r a r u gradu u a r z 1 柱坐标系中 故 u r a u r a r u gradu u ar sin 1 1 球坐标系

1.矢量场的矢量线Φ= d=[Ads= [A.ndS= [AcosodS2.矢量的通量SSSbA.dsdivA3.散度的定义1imAVAV-→O0AQA0A.divAaxayzdivA-V.A4.高斯散度定理:[V.Adv = A.dsS
4.高斯散度定理: V S A dV A d S 1.矢量场的矢量线 2.矢量的通量 3.散度的定义 di A v V A d S S V 0 lim z A y A x A di A x y z v di A A v S S S S d A dS A ndS AcosdS

bA.di=bA cosθ dl1.矢量的环量 「=bA.di2.环量密度limASAS03.旋度的定义矢量A的环流密度的最大值。bA.di10a,a,ClimaacurlA= ×AAs△S→0ofayazAxA,Az$A.di - (V×A.ds4.旋度定理CS5.矢量分析中的两个重要恒等式V.(V× A)= 0V.B=0 =B=VxAE=-VdV×E=0 =V×VΦ=0VxVu=0
1.矢量的环量 C C A d l A cos dl 2.环量密度 S A d l C S 0 lim 3.旋度的定义 x y z x y z A A A x y z a a a curl A A 5.矢量分析中的两个重要恒等式 ( A) 0 B B A 0 u 0 E0 0 E 4.旋度定理 C S A dl A dS S A d l C S 0 lim 矢量 A 的环流密度的最大值。

p:√拉普拉斯算符V.VΦ= X8拉普拉斯算符在各坐标系中的表示式:a?da?da?d直角坐标系:V220x?Oy?oz柱坐标系:101dadQz2Qp?球坐标系:Orr Or1aad1a1Cadv?d(sinr2OrOrr? sin 00a0r? sin? 0p矢量:V?A = (V?A)e, +(V?A )e + (A,)e2025-6-1110
2025-6-11 10 v 拉普拉斯算符在各坐标系中的表示式: 直角坐标系: 2 2 2 2 2 2 2 x y z 柱坐标系: 2 2 2 2 2 2 1 ( ) 1 r r z r r r 球坐标系: 2 2 2 2 2 2 2 2 1 1 1 ( ) (sin ) sin sin r r r r r r v 拉普拉斯算符 : 2 A ( Ax)ex ( Ay )ey ( Az)ez 2 2 2 2 矢量:
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第一章 矢量分析.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第一章 矢量分析.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.1 库仑定律与电场强度 2.2 电位.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.3 静电 场中的导体与电介质.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.4 高斯通量定理.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.5 泊松方程和拉普拉斯方程.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.8 镜像法.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.6 分界面上的边界条件.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第四章 恒定磁场.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.7 唯一性定理.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.9 导体系统的电容.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.10 静电场能量、静电力.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第三章 恒定电场.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第五章 静态场的边值问题.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)复习题题.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第七章 平面电磁波.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)总结复习.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第六章 时变电磁场.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第一章 静电场.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第二章 恒定电场.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第三章 静电场的边值问题.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第四章 恒定电流场.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第五章 恒定磁场.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第六章 电磁感应.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第七章 时变电磁场.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第八章 平面电磁波.pptx
- 《大学物理实验》课程教学大纲 Physics Experiment.pdf
- 《大学物理实验》课程教案讲义(上)物理实验绪论.pdf
- 《大学物理实验》课程教案讲义(上)第一章 测量与误差的基本知识.pdf
- 《大学物理实验》课程教案讲义(上)第二章 常用实验仪器简介.pdf
- 《大学物理实验》课程教案讲义(上)第三章 力学实验.pdf
- 《大学物理实验》课程教案讲义(上)第四章 光学实验.pdf
- 《大学物理实验》课程教案讲义(上)第五章 电学实验.pdf
- 《大学物理实验》课程教案讲义(下)第一章 力、热学实验.pdf
- 《大学物理实验》课程教案讲义(下)第三章 电磁学实验.pdf
- 《大学物理实验》课程教案讲义(下)第二章 光学实验.pdf
- 《大学物理实验》课程教案讲义(下)第五章 设计性实验.pdf
- 《大学物理实验》课程教案讲义(下)第四章 综合实验.pdf
- 《大学物理实验》课程教学课件(PPT讲稿)误差理论.ppt
- 《大学物理实验》课程教学课件(PPT讲稿)热学——导热系数测定.ppt
