西安交通大学：《电磁场与电磁能》课程教学资源（PPT课件）第二章 恒定电场

第二章 恒定电场 + A 序 E E C B 导电媒质中的电流 电源电动势与局外场强 恒定电场基本方程·分界面上的衔接条件 导电媒质中的恒定电场与静电场的比拟 电导和接地电阻

第二章 恒定电场

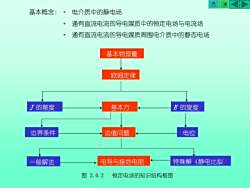
合D基本概念：·电介质中的静电场，通有直流电流的导电媒质中的恒定电场与电流场通有直流电流的导电媒质周围电介质中的静态电场基本物理量欧姆定律E 的旋度J的散度基本方边界条件边值问题电位电导与接地电阻特殊解（静电比拟般解法图2.0.2恒定电场的知识结构框图

基本物理量 J 欧姆定律 J 的散度 基本方 E 的旋度 程 边界条件 边值问题 电位 一般解法 特殊解（静电比拟 ） 电导与接地电阻 图 2.0.2 恒定电场的知识结构框图 基本概念： • 电介质中的静电场 • 通有直流电流的导电媒质中的恒定电场与电流场 • 通有直流电流的导电媒质周围电介质中的静态电场

AKKD2.1导电媒质中的电流2.1.1电流强度单位时间内通过某一横截面的电量，简称为电流。I =dqAdtI是通量，并不反映电流在每一点的流动情况。2.1.2恒定电场的基本物理量电流密度图2.1.1电流面密度失量电流密度是一个失量，在各向同性线性导电媒质中，它与电场强度方向一致。1.电流面密度P分布的体电荷以速度v作匀速运动形成的电流。J=pVA/m?亦称电流密度I=JsJ.ds电流图2.1.2电流面密度

I 是通量,并不反映电流在每一点的流动情况。 1.电流面密度 2.1.2 恒定电场的基本物理量——电流密度 电流密度是一个矢量，在各向同性线性导电媒 质中，它与电场强度方向一致。  电流 I = S J dS 2.1.1电流强度 2.1 导电媒质中的电流 图2.1.1 电流面密度矢量 图2.1.2 电流面密度 A dt dq I = 单位时间内通过某一横截面的电量，简称为电流。  分布的体电荷以速度v作匀速运动形成的电流。 J = v 2 A m 亦称电流密度

合KD2.电流线密度Q分布的面电荷在曲面上以速度<运动形成的电流。K=ovA/m电流线电流(Ken)dl=e是垂直于dl，且通过dl与曲面相切的单位失量工程意义：图2.1.3电流线密度及其通量·同轴电缆的外导体视为电流线密度分布；·媒质的磁化，其表面产生磁化电流可用电流线密度表示，如图示；·交变电场的集肤效应，即高频情况下，电流趋於表面分布，可用电流线密度表示。3、线电流图2.1.4媒质的磁化电流T分布的线电荷沿着导线以速度运动形成的电流I=TV0

• 同轴电缆的外导体视为电流线密度分布； • 交变电场的集肤效应，即高频情况下，电流 趋於表面分布，可用电流线密度表示。 • 媒质的磁化，其表面产生磁化电流可用电 流线密度表示,如图示； 图2.1.3 电流线密度及其通量 工程意义： 图2.1.4 媒质的磁化电流 2. 电流线密度 K =v A m  分布的面电荷在曲面上以速度v运动形成的电流。 I dl l n ( )  电流 = K e e n 是垂直于dl，且通过dl与曲面相切的单位矢量 分布的线电荷沿着导线以速度 v 运动形成的电流I = v 。 3、线电流

AKKD4.元电流的概念元电流是指沿电流方向上一个微元段上的电流，vdvpdy, tds,tdl即Jdy,Kds,Idl。2.1.3欧姆定律的微分形式电场是维持恒定电流的必要条件。可以证明图2.1.6J与E之关系欧姆定律的微分形式。JE式中为电导率，单位s/m（西门子/米）。恒定电流场与恒定电场相互依存。电流J与电场E方向一致。电路理论中的欧姆定律由它积分而得，即U=RI韵思考在各向同性导电媒质中，电位移失量D线与电流密度线方向是否一致？电流线密度K=E是否成立？

2.1.3 欧姆定律的微分形式 • 恒定电流场与恒定电场相互依存。电流J与电场E方向一致。 • 电路理论中的欧姆定律由它积分而得，即 U=RI 欧姆定律的微分形式。 式中  为电导率，单位s/m（ 西门子/米）。 J =E 电场是维持恒定电流的必要条件。可以证明 图2.1.6 J与E之关系 4. 元电流的概念： 元电流是指沿电流方向上一个微元段上的电流， 即 Jdv, Kds, Idl 。 vdq → vdv, vds, vdl • 在各向同性导电媒质中，电位移矢量D 线与电流密度J 线方向是否一致？ • 电流线密度K =  E 是否成立？

合KD2.1.4焦尔定律的微分形式导电媒质中有电流时，必伴随功率损耗。可以证明其功率的体密度为P=J.E(W/m3)一焦耳定律的微分形式电路中的焦耳定律，可由它的积分而得，即(W)焦耳定律的积分形式P-UI-I'R2.2电源电势与局外场强T+2.2.1电源要想在导线中维持恒定电流，必须依靠非静电力将B极板的正电荷抵抗电场力搬到A极板XC。这种提供非静电力将其它形式的能量转为电能装置称为电源。图2.2.2恒定电流的形成

2.1.4 焦尔定律的微分形式 导电媒质中有电流时，必伴随功率损耗。可以证明其功率的体密度为 p = J E （W/m 3 ） ——焦耳定律的微分形式 P UI I R 2 = = 电路中的焦耳定律，可由它的积分而得，即 （W） —— 焦耳定律的积分形式 2.2 电源电势与局外场强 要想在导线中维持恒定电流，必须依靠非 静电力将B极板的正电荷抵抗电场力搬到A极板 。这种提供非静电力将其它形式的能量转为电 能装置称为电源。 2.2.1 电源 图2.2.2 恒定电流的形成

AKKD2.2.2电源电动势与局外场强设局外场强为 E=(V)，则电源电动势为=[Edlq电源电动势与有无外电路无关，它是表示电源本身的特征量。考虑局外场强E7J=Y(E+E)f(E+E).dl=fE·dl+fEdl因此=0+8=8局外场E。是非保守场。图2.2.3电源电动势与局外场强2.3恒定电场的基本方程·分界面上的衔接条件·边值问题2.3.1恒定电场的基本方程

因此 = + =  +  =  +     0 d d d l e l e l (E E ) l E l E l 局外场 Ee 是非保守场。 考虑局外场强 ( ) J = E + Ee  Ee 2.2.2 电源电动势与局外场强 设局外场强为 ，则电源电动势为 d (V) l e = E  l   q e e f E = 电源电动势与有无外电路无关，它是表示电源本身的特征量。 图2.2.3 电源电动势与局外场 强 2.3.1 恒定电场的基本方程 2.3 恒定电场的基本方程 • 分界面上的衔接条件 • 边值问题

AKKD1．J的散度d电荷守恒定律r.ds=Ota在恒定电场中=0散度定理V.JdV=0J.ds=0atJo故V.J=0恒定电场是一个无源场，电流线是连续的。2.E的旋度斯托克斯定理所取积分路径不经过电源，，则E·dl=0[(V×E).dS=0得△XE=0恒定电场是无旋场。3.恒定电场（电源外）的基本方程f,J.ds=0V.J=0J=yEE.dl=0VxE=0·恒定电场是无源无旋场

在恒定电场中 0 t =    = 0  = 0   d dV S V J S J 散度定理 故 J = 0 恒定电场是一个无源场，电流线是连续的。 t q d S    = −  电荷守恒定律 J S • 恒定电场是无源无旋场。 2. E的旋度 恒定电场是无旋场。 所取积分路径不经过电源，则  = 0 ( ) = 0   E dl E dS s l 斯托克斯定理 E = 0 得 3. 恒定电场（电源外）的基本方程  d = 0 s J S  e E dl = 0 J = 0 J =  E E = 0 1. J的散度

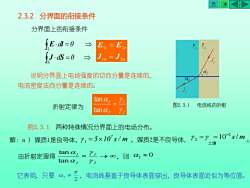
AKKD2.3.2分界面的衔接条件分界面上的衔接条件E·dl=0LE,=E2rYJin=J2nJds=0U说明分界面上电场强度的切向分量是连续的，a电流密度法向分量是连续的。tani=图2.3.1电流线的折射折射定律为tanα,Y2例2.3.1两种特殊情况分界面上的电场分布。解：a）媒质1是良导体，,=5×10’s/m，媒质2是不良导体，Y2==10~s/m土壤tanαYi★8，则α~0由折射定理得tanα2X2要元它表明，只要电流线垂直于良导体表面穿出，良导体表面近似为等位面2

2.3.2 分界面的衔接条件 说明分界面上电场强度的切向分量是连续的， 电流密度法向分量是连续的。 折射定律为 2 1 2 1     = tan tan 图2.3.1 电流线的折射 分界面上的衔接条件 n n t t 1 2 1 2 J J E E =  d = 0  = L E l  d = 0  S J S 例2.3.1 两种特殊情况分界面上的电场分布。 由折射定理得 = →  2 1 2 1     tan tan ，则 2  0 解：a ) 媒质1是良导体， 5 10 s / m 7  1 =  ，媒质2是不良导体, 10 s/ m 。 2 2 −  = = 土壤 它表明，只要 ，电流线垂直于良导体表面穿出，良导体表面近似为等位面。 2 1   

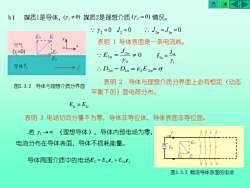
AKKDb)媒质1是导体，（%￥0）媒质2是理想介质（y2=0）情况。:Y2=0 J,=0: J2n=Jn=0EinEi47表明1导体表面是一条电流线。空气(%=0)EitJ2n±0E,=ln:E2n =EY2Yi导体丫..D2n-Din, =&,E2n=0表明2导体与理想介质分界面上必有恒定（动态图2.3.2导体与理想介质分界面平衡下的）面电荷分布。E,=E2表明3电场切向分量不为零，导体非等位体，导体表面非等位面。若Y→0（理想导体），导体内部电场为零本本车电流分布在导体表面，导体不损耗能量。导体周围介质中的电场E,=Eze,+E2ne++++图2.3.3载流导体表面的电场

b） 媒质1是导体， ( 1  0) 媒质2是理想介质 ( 2 = 0) 情况。 0 0 0   2 = J2 =  J2n = J1n = 表明 1 导体表面是一条电流线。 E1t = E2t 表明 2 导体与理想介质分界面上必有恒定（动态 平衡下的）面电荷分布。 表明 3 电场切向分量不为零，导体非等位体，导体表面非等位面。     − = = =  n n n n n D D E J E 2 1 2 2 2 2  2 0 1 1 1  n n J E = 若 （理想导体），导体内部电场为零， 电流分布在导体表面，导体不损耗能量。  1 → E t x E n y E e e 导体周围介质中的电场 2 = 2 + 2 图2.3.2 导体与理想介质分界面 图2.3.3 载流导体表面的电场