《电磁场与电磁能》课程教学课件（MIT，[美]H·A·豪斯J·R·梅尔彻，中译本）第1章 自由空间中的麦克斯韦积分定律

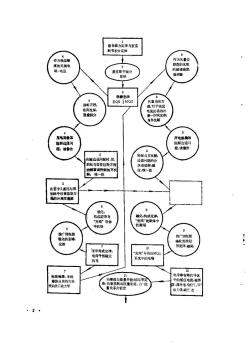
第1章自由空间中的麦克斯韦积分定律1.0引言实践的、智力的和文化的原因促进电学和磁学的研究。用来执行某些工程任务的电系统的工作取决于,至少部分地取决于电的，机电的或电化学的现象。这些应用的电的状况是用麦克斯韦方程组描述的。作为在三维空间里描述电磁场的时间演变，这些相同的方程构成了较在任何其他学科所能找到的更为广泛的现象的简明总结。麦克斯韦方程组是智力的成就，每一个学习物理现象的学生都应熟悉。作为包括连续媒质力学、量子力学、热传导和质量传递，以及许多其他学科的场论的一部分,我们的主题阐述数学的语言和方法,它们是这些其他领域的基础。对于那些对机电能量转换，工频或无线电频率下的传输系统，微波或光频的波导，天线或等离子体有兴趣的人来说，不需要去论证成为处理电磁场问题的专家的必要性。另有一些人可能需要鼓励。例如，电路设计者也许满足于电路理论，它的定律用电压和电流，以及电路元件对电压和电流的约束关系来阐明。然而，这些定律在高频时失效，因而不用电磁场理论就不能理解这点。当频率增加到这样高，使电磁场的传播时间变得可与一个周期相比附，电路模型的局限性开始起作用，结果是“电感器”表现为“电容器”或反之。其他的局限性与损耗现象有关。随着频率的增加,电阻器与晶体管被“电容”效应所限制,而变流器与变压器被“涡”流所限制。任何一个与提出物理系统的电路模型有关的人都需要有场论的基础，以证明近似是正确的并得出电路参数的值。因此，与心电图学或神经生理学有关的生物工程师在建立物理现实与模型之间有意义的联系，并把这些模型用电路元件表示时，必须借助于场论。类似地，即使控制理论家利用集总参数模型，它的正确性也依赖于连续媒质理论，不论性质上是电磁的，机械的或热的。计算机硬件似乎是不依赖于电磁场理论的另一个应用。我们往往通过软件接口才注意到计算机，使得我们认为计算机似乎与我们的主题无关。虽然硬件通常用电路来实现，但用来完成逻辑运算的计算机的实际实现是被电磁定律所限制的。例如，起源于计算机中某一处的信号不可能在小于一个以光速传播的信号通过连接导线所需要的时间内到达另一处。随着计算速度的增加，电路模型仍保持有用对固体技术是个贡献，从而使基本电路元件的尺寸减小成为可能。由电磁场施加的基本限制终究会确定计算机技术的计算速度极限，不论它是由电磁波延迟或是由电功率损耗所引起的。内容概述如图1.0.1中的图解说明所示，我们从积分形式的麦克斯韦方程组开始。本章从用力和源所表示的场的定义开始，继之以各个积分定律的回顾。与论述紧密结合的是一些例题，这些例题1

洛仑兹力定律与麦克节积分定作为电信梯度的无炭电欢磁通场：电压常克违静态EOS/MQ拍热为;我好学给定商异性屏异性明电满叠加用电流强无：镜像页，蟑费法尚题自松亏拉普拉斯方程相齐肉舒在信卡红翻技与方家卡儿的分离交墨解路1E的传导构成定律“完纯“导体的MQS电徒守恒稳定系统中的电场传导电导率有限的导电荷苑线的品能产的感应电选：带洗的依分岛的：特导电片的/系大段学：磁2

太片漫的动态用铭您求边2从边值观点看动态场玄尔姆医益方程TEM,TM与TE波导模式；金属与介质波导修数模型给线新力学磁场图1.0.1内容略图。所示三栏分别是关干准静态电学，准静态磁学与电动力学，表明论述尽相对应的。用来阐明在陈述积分定律时要用的面积分和体积分方法。例题也企图使每一个定律至少与一种物理情况相联系。在以后儿章中我们的目的是使这些定律有用，不仅是在模拟工程系统，而目也在以定性的方式处理实际系统时(如伺发明者经常做的那样)。在以下三种情况下：(a)以这种定性的方式处理场时，b)为对称的简单图形求场时，（c)把场与它们的源相联系时，积分定律是直接可用的。第2辜从积分定律导出微分的描述。然后通过与每一节相联系的例题和·些家庭作业，润述了数学定理和算子的最低限度的基础知识。微分算子以及相关的积分定理在需要时引人。因此，散度和旋度算子，与高斯定理和斯托克斯定理一起在第2章中提出，而梯度算子和积分定理自然是在第4章中导出。在深入理解由麦克斯韦方程组所顾见的现象时，静态场往往是第一个题目。场是不可测量的，更不用说实际关心了，除非它们是动态的。象这里所论述的，场决不是真证静态的，任第3章开如的准静态学的题，对于我们理解麦克斯韦方程组的含意所用的方法是重要的。当我们学会忽略无关紫要的混杂时，才能达到对这些方程的完全理解，如果时问变化率足够慢（顿3

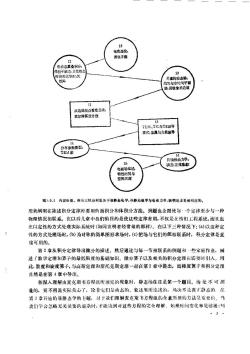
率足够低)，以致由于电磁波的传播引起的时间延迟成为不重要时，电准静态的(EQS)和磁准静态的(MQS)近似法证明是正确的。第3章所考案的一些例子，可使人们大溉地知道，对于一种给定的情况,这两类近似法中的哪-一类是合适的。当在第 11至 15章中把 EQS 和 MQS移到一起加以论述时，对准静态近似法的全面评价将提到面前。虽然电容器和电感器分别是电准静态和磁准静态范畴的例子，但准静态系统通常能用与频率无关的电路元件来模拟的说法是不正确的。品体管的高频模型正确地以EQS近似为基础。晶体管中的电磁波延迟是不重要的。但是，动态效应是重要的,而 EQS 近似能包括电荷移动的有限时间。涡流屏蔽或加热器的模型正确地以MQS近似为基础。电磁波的延迟时间仍然是不重要的，而最重要的磁场的渗透时间用MQS定律描述。作用于电子束的空间电荷波或饱和磁化材料中的自旋波，即使所考的频率在吉赫范围内，也往往分别用EQS和MQS定律描述。EQS系统（第 4-7章）和MQS系统（第8—10章）的对应的论述通过图 1.1. 0. 1 的第-一页可明显地看出。对于左边EQS栏中的每一个题目，在MQS栏中相同的位置处有一个类似的题目。虽然场的概念以及在处理EQS和MQS 系统中所用的数学方法常常是相似的，但是比较研究展现出与直接类比同样多的差异。在电的与磁的研究之问，有双向的相互作用。不仅论述EQS系统得到的结果可应用于描述MQS系统，而且对MOS情况的检验导致对EQS定律的更多了解。在图1.0.1的第一页，EQS和MQS两栏的顶端，给出了电场和磁场的一般（对比的)特性。然后论述从场源是规定的情况转到场源是待定的情况，因此，从给定的电荷分布首先求得EQS电场，而MQS磁场是由给定的电流确定的。EQS场解答的推导过程为以后的MQS的推导直接作了准备，在许多实际情况中，认为这些源是在材料中感生出的，因而必须作为场的解答的一部分求出。这些情况中的第一个是，感生的源是在具有足够高电导率的导体边界上，这种导体可以用“完纯”导体作为模型。对于EQS系统，这些源是表面电荷；而对干MQS系统，它们是表面电流。在任何一种情况下，场必须满足边界条件，并且EQS的研究不仅提供数学方法，而且甚至提供可直接应用于MQS问题中的偏微分方程。极化与磁化说明能被确定的场源（驻极体与永久磁铁）或由场本身所感生的场源的原因。在此处所用的朱氏表示法中，极化与磁化的阐述方式之间有完全的类比。因而，从第6章到第9章有概念的直接转移。平行的准静态的研究以在第7和10章中对损耗现象的检验而告终结。此处我们知道对一方面是 EQS，而另一方而是 MQS 所提出的“导体什么时候是完纯的！"问题，必须给出很不同的答案。在第11章中，以前提出的许多概念通过研究功率流，能量储存和电磁力的产生而得到应用。由此章开始，不再近似地应用麦克斯韦方程组。从而注意到在 EQS 和 MQS 近似所表示的系统中，分别是电能量储存或是磁能量储存占支配地位。在第12至14章中，焦点集中于电磁波。其发展过程是EQS和MQS两栏中包含的方法的自然扩展。它用图1.0.1第二页上的略图来突出地表示。第12和13章的题目对应于前页EQS和MQS两栏的题目。用来表示电动力学场的电位是EQS和MQS系统中所用电位的白然推4

广。如同在准静态场中那释，首先考虑给定源的场。闪此紧接的实际应用是天线的辐射场的描述。在第5章中对EQS系统以及在第8章中对MQS系统引人的边值观点，是第13幸的基本主题。实际例子包括简单的传输线与波导。对第14章的内容即传输线动力学的理解，在处理用来模拟大多数高频率系统的“传统”理想传输线时是必需的。对于表示准静态动力学过程，它们也显示出能提供有用的模型。要实际应用麦克斯书方程纽，必须掌撑取近似的技巧。根据系统的电磁特性和数，以及重要的时问尺度（频率），一→个物理系统如何能被分成电磁子系统，每一个子系统如何用它的要的物理过程来描述考虑纠这个目的，在第3章中引人了EQS和MQS近似法，并且为此第15章给出了电磁场的综述。1.1自由空间中的洛仑兹定律阐述电动力学理论有两种观点。较老的一种观点认为，两个电荷或电流之间的吸力或斥力是超距作用的结果。静电学的库仑定律以及静磁学的对应的定律就是首先以这种方式叙述的。法拉第1"提山一个新方法，他想象在相互作用着的电荷之间的空间中充满场，由于场的存在，在某种意义上空间被激活；按照法拉第的观点，两个相互作用着的电荷之间的力在相互作用着的物体之间的空间中从一个体积元到一个体积元地被传递，直到最终它们从一个电荷被传递到另一一个电荷。法拉第方法的优点将当时已充分发展的连续媒质力学理论应用于电磁问题。这一观点的确立是麦克斯书对以他的名字命名的方程组的系统地阐述[2]根据法拉第的观点，在「处电场与磁场是确定的，即使当该处不存在电荷时。根据作用在试验电荷9上的力可以确定场，如果是在所关心的时间以速度运动被引人到r处。用实验方一部分与无关，而另一部分与成正比且垂直于它。力由洛法求得这样的力由两部分组成，仑兹力定律用电场强度E和磁通密度*uoH表示。（用作失量运算的复习，见附录1。）f=q(E+xμH)(1)组成式(1）的电力与磁力的叠加用图1.1.1加以说明，图中包括用来决定和μ.H的叉积方间的右手定则的提示。一般说来，E和H不是均勾的，而是位置r和时间t的函数：E：E(r,t)和μH=μH(r,t).除了与力学有关的长度、质量和时间的单位之外，按照电动力学需要电葡的单位。这个单位足库仑(C)。于是洛仑兹力定律式(1),可用来确定E和μsH的单位。要（）-工克*/梦（kgm/）(2) E的单位一库会()库仑（C顺（N)l 的性位一原色素增(Cm)一原香糖(%(3)我国有时也采用术语磁感应强度，译者注:5

gvxunUX图 1.11.1 仑蒸力F 与电场强度E,磁场强度H 和电脊速度的几何关系。 (a)电力,(b)磁力和(e)总力。根据力定律，我们只能建立磁通密度 μH的单位，直到1.4节才能论证H的导出单位为安培/米(A/m),从而μo的单位为亨利/米(H/m)。在大部分电动力学中，根据自身的理由，主要关心的不是力学而是电场和磁场。因此在核对一些量的单位时使用质量的单位是不方便的。对电场强度的单位引人一→个新的名称一一伏特/来(V/m)证明是有用的。在本章最后表1.8.2中给出的变量小结中，基本单位都是SI(国际单位制），而导出单位利用这一事实，使质量的单位千克=伏特一库仑一秒*/来*(kg=V.C.s/m")，并且库仑/秒=安培(C/s=A)。如果采用基本单位,方程量纲的核对是保证的，但在使用导出单位时也往往能达到目的。 后者联系了变量的物理性质与电的和磁的变量的固有对称性。例1,11。电子在有均匀静电场的真空中的运动在真空中，带电粒子的运动仅受到它本身惯性的限制。在图1.1.2所示的均勺电场中，不存在磁场，一个电子从0平面以初速出发外施”电场易为E=，式中为“方向的单位失量而。为一已知常数。这里要确定轨迹，并用来作为例1.2.1中电荷与电流密度的例证。如定义㎡为电子质量，牛顿定律结合洛仑兹定律来描述运动有图1,1.2承受均勺电场强度 E,的电子，对于正电场和负电场具有所示的作为时间函(4)数的位置电子的位置示于图1.1.2。电子电荷照例用e(e=1.6×10-9C)表示，式中是正的，因此式(4)中需要加上负号。通过两次积分，我们得5,=-$E,+0t+0式中e:与 o为积分常数。假定当时，电子是在5.-0处并有速度，由此得出这些常数为e=DI+量B+i0--t-2mBt于是，电子的位置与速度可以时间的函数形式表示为(7).=B(-t)"+u(-t)

--元8.(6) +0,(6)如规定为向上的，且B.>0，电子在电场中的运动类似于物体在重力场中的自由降落，如图1.1.2所示。“F<0，且初速也是正的时，速度是单调地增加的时间函数，也示于图1.1.例1.1.2.电子在有均匀静磁场的真空中的运动洛仑兹力中磁的贡献，既垂直于粒于速度，又垂直于外施场。我们通过考察由沿？轴的初速产生的轨道来说明这一事实。当均句恒定的磁通密度 uH 洛轴存在时，力为-e(UXuH)(9)量因子，所以由磁场引起的电子的加速度总是垂直于它的速度。因此，仅有磁两个失量的叉场不能改变电子速度的量值(因面也不能改变电予的动能），面仪能改变速度的方向。因为磁场是均幻的，又因为速度和速度的变化率位于垂直于磁场的平面内，最后，还因为的量值并不改变，我们得出加速度有恒定的量值，并且与速度和磁场都正交。电子在圆周上运动，以致离心力与磁力相平衡。图1.1.3a说明此运动。圆周的半径可通过使离心力与径向洛仑慈力相等来确定eμ:[o| H,-mo?(10)上述问题可加以修正以计及速度与磁场之间的任意初始角。矢量运动方程（实际是三个未知量、5、多，的三个方程）图1.1.3a）在均匀磁遵密度H，以方专：没有初速时，电子有匾形轨道。（b）在%-X)(12)方向有初速时，轨道是螺旋形的就5而言是线性的，所以解答可以查加以满足初始条件，它不仅包括速度，而且也包括方向的速度#。磁场同方向的运动不产生附加的力。因此，式(12)右边的9分量为零。积分则表明3方向的速度保持为它的初始值 9不变。这一均匀运动可以加到已经得到的结果上，从而看出电子沿着螺旋形的路径运动，如图1.1.3b所示得注意的是电子围绕着场旋转的角频率与电子的速度无关，而仅与磁通密度。H。有关。确实，从式（11)我们求得(13)HH磁通密度为1V-s/m或1 特斯拉(T)]时,回旋显率为f=0/2元=28GHz。 (对于个电子，8=1.602×10-18C和m=9.106×10-31kg，）当z方向的初为3×107m/s时，在磁通密度uH=1T的情况下，回施半径r0j2/0。=1.7×10-* m,1.2电荷密度与电流密度在发克斯韦时代并不知道电荷不是无限可分的，而以1.6×10-18C即电子电荷为基本单位出现，因此，麦克斯韦的宏观理论涉及连续电荷分布。对于由大量的基本电荷的聚集所产生的工程意义的场，这是恰当的描述。这些紧集产生的电荷分布，可以方便地用单位体积的电荷，即电荷密度p来描述。.79

取一增量体积并确定其内部的净电荷。则p(r, t)=AV 中的净电荷(1)是时间为t时在位置r处的电荷密度。p的单位为库仑/来(C/m)。体积AV要选得比所考虑的系统的尺寸小很多，但又要大到足以包含许多基本电荷。把电荷密度β作为位置的连续函数来处理。在这样的“宏观”处理中，忽略了电荷分布的“颗粒性”从根本上说，电流是电荷的迁移，并包含电荷的时间变化率的意义。电流密度是有向的每单位面积的电流,因i而用(库仑/秒) / 米[(C/s) /m门来度量。 电荷密度 p以速 度 运动意味若每单位面积的电荷迁移率，即电流密度J，可由下式给出(2)=pu设想这一关系的一种方法示于图1.2.1,图中具有速度的电荷密度p通过微分面积8a。面元有单位法线n，因此微分面积矢量可以定义为oα=noa。在微分时间dt内通过的电荷等于在体积&adt内包含的电荷。于是d(8g) pv.Sadt(3)除以dt,我们预料到式(3)会取 J.oa 的形式,从而得到由式(2)所表示的电流密度与电荷密度的关系速度是电荷的速度。电荷究竞怎样开始运动与物理情况有关。电荷可能悬浮在绝缘物质中或在它的上面，而绝缘物质本身在运动中。在这种情况下，此速度也就是物质的速度。很可能，这是将电场施加于导体的结果，如第7章中所要考虑的。对于在真空中运动的带电粒子，它可能起因于用牛顿定律和洛仑兹定律表示的运动,如 1. 1 节中的例子所述。下例就是这种情况。T」通过具有法向a的表面。图1.2.2电荷在下边界注人并归电场加速向上。(a)91.2.1电流密度电场预度，（b)速度和！c)电荷密度的垂直分布。例1.2.1.真空二极管中的电荷密度与电流密度考虑由r-0平面内的阴极“以初速发射的电子的电荷密度与电流密度，如图1.2.2a所示。电子是选续地注入的。如同在例1.1. ！中，所考虑的是个别电子的运动,且假定电场是均匀的。在下一节中,将认识到电荷是电场的源。这里假定用来施加均勾场的电荷，比起与电子有关的空问电荷”要多得多。在低电子电流的限度内这被认为是合理的。任一电子具有由式(1.1.7)和(1.1.8）给出的位置和速度。若每一个电子以相同的初速射人，则可预期在任一给定的=常数平面内电荷密度和电流密度将与时间无关。此外，通过任何平面的电流应与通过任何其他这种平面的电流相园。这就是说，在稳态，电流密度不仅与时间无关，而且也与无关，因此，可以写成①这里我们设想场变母，和p好象都是正的。对于电子，00，必须有E，0，.8

(4)p(a)(a) J式中J。是络定的电流密度。以下的步骤说明这一电流连续性条件如何能够使得用时间作为自变量来描述粒子运动的叙述转变到用垒标(s, ,2)(或缩写为r)为自变量的叙成为可能。由式(1,1.7）所指述的电子的射间与位置间的关系取(1-)二次方的形式=B(-)(-)+-0此方程可以求解以得出粒子到达位置。所消逝的时间。注意在式(5)的两个可能的解答中，选择满足当1=1时,，=0 的那个解答01-0-2%8.5(6)t-tSR.利用此式，由式（1.1.8)给出的速度可以写成deo--2Ens.(7)现在我们转变观点。在式(7)的左边是在位置。一处粒了的速度。置换变量则得(8) -0-22E1因此成为用来表示因变量0。的自变盘。由上式与式(4)得到电荷密度(9) V好一华E也是表示成的函数。图1.2.2中所示的曲线是假定E，<0，因此电子具有的速度随单调增长。如所预期的，电荷密度随2的增大而减少，因为当它们加速时，电子变得稀少以保持电流密度不变。1.3电场强度的高斯积分定律1.1节的洛仑兹力定律表达了电磁场对运动电荷的作用。本章中剩余的几节与运动电荷对电磁场的反作用有关。要考虑的麦克斯书方程组的第一式即高斯定律，它描述电场强度如何与它的源相关。出表面S包围的任意体积V内的净电荷与穿过该表面的净电通量的关系为(1)f,oE.da-,pde图1.3.1中所示体积，其表面的法线规定为向外指。式中自由空间的介电常数e=8.854x10-12法拉/米(F/m)，它是用SI单位表示麦克斯韦方程组时所需要的一个实验常数。在式(1）的右边是被表面S包围的净电荷。在左边是遍及这同一闭合表面的通量.E·da的微分贡献的总和。图1.3.1包国体积Y的一般表面8。量eE称为电位移通注密度，并E出式(1)）单位为库仑/米(C/m)。在任何包含净电荷的风域外面，一定有净电位移通量

下面的例了说期进行体分和积分的技巧。例1. . 1.。 球对称电萄分布引起的电场给定「电背与电流分布后，积分定律就可究全地确定电场与磁场。然而，它们并不是直接有用的，除非是很一个例子是图1.3.2的球坐标系统中电荷密度分布为对称的情况。fPR<R(2)图1.3.2球对称电荷分布，表示电荷密度以及和关的径向电场强度与半径的关系。(b) 用来说明 E的恢截经向坐标的分量为零的旋转轴。这里P，和R是已知常数。根据球对称性的论证表明唯一可能的E的分量是径向的。E=i,E,(n)(3)确实,假定除了这个↑分量之外,场还有一个与分蛋。 则在一给定点，E 的分量就表现为如图 1. 3. 2b 所示。 所示的系统绕轴旋转导致在某一垂直于，的新方向形成E的分量。然而，旋转使该场的源，即电荷分布不变。可见 E。必须为零。类似的论证表明 E。也为零。增量体积元为(dr) (rdo) (rsintdg)(4)出此可得山具有任意半径“的球体租Jj[]sind)(rdodr(5)l(r' sind) (r'do)drp,R; R<rJ.J,J.Po'R计算（1)式的左边，注意到i,(rd) (rBinode)(6)这样，在任意半径+处的球表面$rE.da-fTE,(rsindb) (rd) -B,4mr!(m借助予(5)和(7)两式中求得的作积分和面积分，高斯定律式(1)表明,4a-R-E,=PARr<R(8a)tE.4rxp.RsE,-Pir<r(8b)在球形带电区域内，径向电场强度随平轻的平方而增加，因为即使相关的衣面象卡径的平方那样增长，它所包围:10