《电磁场与电磁能》课程PPT教学课件（马冰然版）第二章 静电场 2.5 泊松方程和拉普拉斯方程

第二章2.52.5泊松方程和拉普拉斯方程牛 静电巧的基本方程：线性、均匀、各向同性电介质fE.di -0无旋：积C分fD.ds =q有散V×E=0微分V.D=p本构关系D==,=+P2025/6/11

2025/6/11 第二章 2.5 1 2.5 泊松方程和拉普拉斯方程 静电场的基本方程: 线性、均匀、各向同性 电介质     =  = s c D ds q E dl     0 积 分 无旋： 有散  =   = D E   0 微 分 本构关系： D E r E E P      =  =  0  =  0 +

第二章2.5泊松方程和拉普拉斯方程：正泊松方程：X：静电场为无旋场，故可引入Φ标量电位来描述之。而V.D=p将D= 及 E=-VΦ 代入上式中V.sE=pV.E-P即8d泊松方程V.Ve=-P8(2-5-1)P822025/6/11

2025/6/11 第二章 2.5 2 泊松方程和拉普拉斯方程： ❖ 泊松方程： ∵ 静电场为无旋场，故可引入一标量电位  来描述之。 而  D =   将 D = E 及 E = − 代入上式中    即            = −  = −  =  = 2 E E   （2-5-1）  的泊松方程

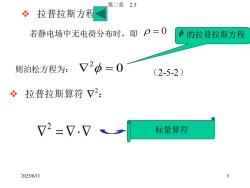
第二章2.5拉普拉斯方程X若静电场中无电荷分布时，即β=0D的拉普拉斯方程2Φ=0V2则泊松方程为：(2-5-2)拉普拉斯算符√2：XV?=V.V标量算符32025/6/11

2025/6/11 第二章 2.5 3 ❖ 拉普拉斯方程： 若静电场中无电荷分布时，即  = 0 则泊松方程为： 0 2   = （2-5-2）  的拉普拉斯方程 ❖ 拉普拉斯算符  2 ：  =  2 标量算符

第二章25拉普拉斯算符在各坐标系中的表示式：a?aa?p直角坐标系：Oy2Qz2Ox?柱坐标系：1 aaa~dOrQz2aor OrF球坐标系：1a1adadadCsinaOrOra0sin?0 p4sin00042025/6/11

2025/6/11 第二章 2.5 4 ❖ 拉普拉斯算符在各坐标系中的表示式： 直角坐标系： 2 2 2 2 2 2 2 x y z  +   +    =     柱坐标系： 2 2 2 2 2 2 1 ( ) 1 r r z r r r   +   +      =      球坐标系： 2 2 2 2 2 2 2 2 1 1 1 ( ) (sin ) sin sin r r r r r r                 = + +     

第二章2.5求解泊松方程（或拉普拉X斯方程）：Φ=E给定电荷分布，求解其方程得(:E=-VΦ)若已知E、D→ p2025/6/11

2025/6/11 第二章 2.5 5 ❖ 求解泊松方程（或拉普拉 斯方程）： 给定电荷分布，求解其方程得 E    若已知 E D 、   （ ） E = −

第二章2.5例：若半径为a的导体球面的电位为U。，球外无电荷，求空间的电位。解：显然，导体球的电荷分布在球面上，且呈球对称,故空间的电位也呈球对称,仅是r的函数。 取球生标系。因球外无电荷，则空间电位满足拉普拉斯方程0= 0球坐标系中drQdp即drdr2025/6/11

2025/6/11 第二章 2.5 6 例：若半径为 a 的导体球面的电位 为 U0 ，球外无电荷，求空间的电位。 解：显然，导体球的电荷分布在球面上， 且呈球对称，故空间的电位也呈球对称， 仅是r 的函数。取球坐标系。 因球外无电荷，则空间电位满足拉 普拉斯方程 0 2   = 球坐标系中 ( ) 0 1 2 2 = dr d r dr d r  即 2 1 1 2 r C dr d C dr d r =  =  

第二章2.5CdpdoCIdrdrC+C,DrCi +C,而 r=a时，β=U。=-ar=8时,=0=C2 C,=-aUaU.故0=72025/6/11

2025/6/11 第二章 2.5 7 C2 r C 1   = − + 2 1 1 2 r C dr d C dr d r =  =   2 1 , C a C r = a时  =U0 = − + 0 2 r = 时,  = =C 而 0 C1 = −aU r aU 0 故  =

草例：两无限大平行板电极，板间距离为d，电压为U。，并充满密度为Po 的体电荷。求板间电场强度和极板面上的申荷面密度。如图！(d)E(x)解：两平行板电极无限大，若其间无电荷分布，则板间电场强度均匀;PoxxPoxdd的而实际上板间充满密度为d11体电荷，由于体电荷只是x的U.0函数,故申场强度也只是X的函数。应用高斯通量定理求解。>作一柱形闭合面为S，底面积为 △S，下底在左极板内，上底在X处，侧柱面与a.平行。2025760

2025/6/11 第二章 2.5 8 ➢ 两平行板电极无限大，若其 间无电荷分布，则板间电场强度 均匀; 而实际上板间充满密度为 的 体电荷，由于体电荷只是 的 函数， 故电场强度也只是 的函数。 d x  0 x x 例：两无限大平行板电极，板间距离为 ，电压为 ，并充满 密度为 的体电荷。求板间电场强度和极板面上的电荷面密 度。如图。 d U0 d x0  解：  应用高斯通量定理求解。 ➢ 作一柱形闭合面为S，底面积为 ，下底在 左极板内，上底在 处，侧柱面与 平行。 S x x a  x d E(x) d x  0 (d) s  0 U0

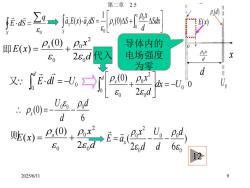
第二章　2.5(d)Zq[aE(x)d(0)+fE.ds-OC&0SPox?导体内的即E(x)= P,(0) Por代入电场强度x26.d&od为零1d1p,(0)Pox又"E.diEU.dx280d&oUcoPod: p.(0)6dP,(0)PoxU.Podx则E(28.d%d66091292025/6/11

2025/6/11 第二章 2.5 9 (0) s  0     = q E dS S          =  +    x x s S x Sdx d x a E x a dS S 0 0 0 (0) 1 ( )      即 d x E x s 0 2 0 0 2 (0) ( )     = + 又  0 0 E dl U d  = −    代入 0 0 0 2 0 0 2 (0) dx U d d x s = −       +      6 (0) 0 0 0 d d U s     = − − 则 d x E x s 0 2 0 0 2 (0) ( )     = + ) 2 6 ( 0 0 0 0 2 0     d d U d x E ax = − −   12 导体内的 电场强度 为零 x d E(x) d x  0 (d) s  0 U0

第二章2.5>作一柱形闭合面为S，底面积为AS下底在左极板内，上底在x>d极板内p.(d)侧柱面与 a平行。fE.ds-Zq60S闭合面上、下底处PorIlx的电场强度为零，d/侧面的法向与电场.g=011故dU.强度的方向垂直 Po-ASdx + p,(d)AS = 0P. (0)AS +JodU.cPodp,(d)则d3102025/6/11

2025/6/11 第二章 2.5 10 ➢ 作一柱形闭合面为S，底面积为 ， 下底在左极板内，上底在 极板内， 侧柱面与 平行。 S x a  x > d 0 0  = =    q E dS S   闭合面上、下底处 的电场强度为零， 侧面的法向与电场 强度的方向垂直。 故 q = 0 (0) ( ) 0 0 0  +  +  =  Sdx d S d x S s d s    则 3 ( ) 0 0 0 d d U d s    = − x d d x  0 (0) s  (d) s  0 U0