《电磁场与电磁能》课程PPT教学课件（杨儒贵版）第八章 平面电磁波

麦克斯韦方程静态场中的高斯定理及磁通连续性原理对于时变电磁场仍然成立。那么，对于时变电磁场，麦克斯韦归纳为四个方程，其积分形式和微分形式分别如下：积分形式微分形式aDaD全电流定律H.dL-.dsVxH=J+atataBaB电磁感应定律E.dl:.dsVxE=atat磁通连续性原理Φ. B.ds=0V.B=0厂高斯定律, D.dS=qV.D=papV.J=D=&EB=μHJ=oE+J'at

麦克斯韦方程 静态场中的高斯定理及磁通连续性原理对于时变电磁 场仍然成立。那么，对于时变电磁场，麦克斯韦归纳为 四个方程，其积分形式和微分形式分别如下： d ( ) d l S t   = +     D H l J S d d l S t   = −     B E l S d 0 S  =  B S d S  = q  D S 积分形式 t   = + D H J t    = − B E B = 0   D =  微分形式 全电流定律 电磁感应定律 磁通连续性原理 高斯定律 t    = −  J D =  E B =  H J = E + J

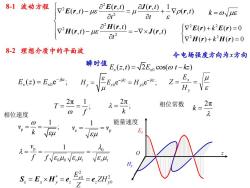
8-1 波动方程αE(r,t)aJ(r,t)1?E(r,t)--Vp(r,t)k=のyueL18at?at8o°H(r,t)?E(r)+k?E(r)= 0V"H(r,t)-μeVxJ(r,t)at?V?H(r)+kH(r) = 08-2理想介质中的平面波令电场强度方向为x方向瞬时值 E,(z,t)= /2Exo cos(α t-ke)DEμ0E(z) = Exoe-jks;H.E.H,N8u2元2元12元相位常数T :1=k0元相位速度1能量速度10VpVe2RExkJeuVsu12V.20fcoeuVeH,E2oe.ZH?S =E xHvoZ

8-2 理想介质中的平面波 8-1 波动方程        = −    − +    =    − ( , ) ( , ) ( , ) ( , ) ( , ) ( , ) 1 ( , ) 2 2 2 2 2 2 t t t t t t t t t t J r H r H r r E r J r E r           + =  + = ( ) ( ) 0 ( ) ( ) 0 2 2 2 2 H r H r E r E r k k 令电场强度方向为x方向 瞬时值 0 ( , ) 2 cos( ) E z t E t kz x x = −  j 0 ( ) e ; kz E z E x x − = 2π 1 T ;  f = = 2π ; k  =  2π k = p 1 v ; k   = = r r 0 0 0 r r p 1         = = = f f v   = = y x H E Z 2 0 2 * 0 c z y x x y z ZH Z E S = E  H = e = e e p 1 v = = v  j j 0 0 e e ; kz kz H E H y x y   − − = = O z Hy Ex 相位常数 能量速度 相位速度 k = 

E,(z,t)= ~2Ero cos(o t-kz)均匀平面波k=のuskz时间相位：のt空间相位：波面空间相位相等的点组成的曲面称为2元_1T:时间相位のt变化2元所经历的时间。周期（T）)f0一秒内相位变化2元的次数。频率 ()元=2元空间相位kz变化2元所经过的距离。波长 ()k相位常数k表示单位长度内的相位变化。又称为波数2元k=dz_0元相位速度VVpdtk根据相位不变点的轨迹变化可以计算电磁波的相位变化速度，Eu这种相位速度以v表示@ t-kz = const7波阻抗电场强度与磁场强度之，以Z表示H,V&横电磁波，TEM波对于传播方向而言，电场及磁场仅具有横向分量Sav1能量速度2=VpV.WavVeu

均匀平面波 0 ( , ) 2 cos( ) E z t E t kz x x = −  时间相位:  t 空间相位: kz 波面 空间相位相等的点组成的曲面称为 周期（T ） 时间相位 t 变化 2 所经历的时间。 f T 2π 1 = =  频率（f ） 一秒内相位变化2 的次数。 波长（ ） 空间相位kz 变化 2 所经过的距离。 k 2π  = 相位常数 k 表示单位长度内的相位变化。又称为波数  2π k = 相位速度vp t k z v  = = d d p 波阻抗 电场强度与磁场强度之，以Z 表示   = = y x H E Z 横电磁波，TEM波 对于传播方向而言，电场及磁场仅具有横向分量 能量速度 av av e w S v = e p 1 v = = v  k =  根据相位不变点的轨迹变化可以计算电磁波的相位变化速度， 这种相位速度以 vp 表示  const t kz − =

缩波效应已知平面波的频率是由波源决定的，但是平面波的相速与介质特性有关。因此，平面波的波长与介质特性有关。1由上求得2=p+fcooVerurVou01式中MokfJeoo孔o是频率为f的平面波在真空中传播时的波长。可见，几<几。。这种现象称为波长缩短效应或缩波效应。折射率：光在真空中的速度与光在该材料中的速度之比率

已知平面波的频率是由波源决定的，但是平面波的相速与介质 特性有关。因此，平面波的波长与介质特性有关。 r r 0 0 0 r r p 1         = = = f f 由上求得 v 式中 0 0 0 1    f = 0 是频率为f 的平面波在真空中传播时的波长。 可见， 。这种现象称为波长缩短效应或缩波效应。   0 缩波效应 p 1 v ; k   = = 折射率：光在真空中的速度与光在该材料中的速度之比率

色散(()+)'=08-3.导电介质中的平面波电场强度可写为k=0/[/()-1E,=Eroe-jk==Ere-k"e-jks式中第一个指数表示电场强度的振幅随2增加不断衰减，第二个指数表示相位变化。因此，k称为相位常数，单位为rad/m；k"称为衰减常数，单位为Np/m，而k.称为传播常数。0导电介质中的相速为k可见，相速不仅与介质参数有关，还与频率有关各个频率分量的电磁波以不同的相速传播，经过一段距离后各个频率分量之间的相位关系将发生变化，导致信号失真，这种现象称为色散。所以导电质又称为色散媒质

k z k z x k z Ex Ex E − −  −  = = j 0 j 0 e e e c 电场强度可写为 式中第一个指数表示电场强度的振幅随z 增加不断衰减，第二个指 数表示相位变化。因此，k 称为相位常数，单位为rad/m；k 称为 衰减常数，单位为Np/m，而kc 称为传播常数。 导电介质中的相速为          +      + =   = 1 1 2 1 2 p     k v 可见，相速不仅与介质参数有关，还与频率有关。 各个频率分量的电磁波以不同的相速传播，经过一段距离后， 各个频率分量之间的相位关系将发生变化，导致信号失真，这种 现象称为色散。所以导电质又称为色散媒质。 8-3. 导电介质中的平面波 色散 1 1 2 2          +       = +    k  1 1 2 2          −       = +    k 

集肤效应8-3.导电介质中的平面波具有低电导率的介质第一AAk"_ok'=o/ue7.0>08R电场强度与磁场强度不同相，且因。较大，两者振幅发生急剧衰减，以致于电磁波无法进入良导体深处，仅可存在其表面附近这种现象称为集肤效应场强振幅衰减到表面处振幅的深度称为集肤深度，以表1示，则由e-hs=e-1S=k"元fuo可见，集肤深度与频率f及电导率成反比

8-3. 导电介质中的平面波 集肤效应   第一 电场强度与磁场强度同相 k =     2 k = c   Z = 第二   具有低电导率的介质 良导体 π 2   k = k = = f     f Z π (1 j) j c =  + 场强振幅衰减到表面处振幅 的深度称为集肤深度，以 表 示，则由 e 1 1 e e −  − = k    k πf 1 1 =  = 可见，集肤深度与频率f 及电导率  成反比。 电场强度与磁场强度不同相，且因 较大，两者振幅发生急剧 衰减，以致于电磁波无法进入良导体深处，仅可存在其表面附近， 这种现象称为集肤效应

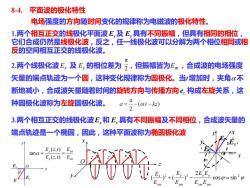
8-4.平面波的极化特性电场强度的方向随时间变化的规律称为电磁波的极化特性1.两个相互正交的线极化平面波E，及E，具有不同振幅，但具有相同的相位它们合成仍然是线极化波，反之，任一线极化波可以分解为两个相位相同或相反的空间相互正交的线极化波。2.两个线极化波E，及E，的相位差为，但振幅皆为Em，合成波的电场强度矢量的端点轨迹为一个圆，这种变化规律称为圆极化。当增加时，夹角α不断地减小，合成波失量随着时间的旋转方向与传播方向e.构成左旋关系，这元种圆极化波称为左旋圆极化波。-(wt-kz)a=23.两个相互正交的线极化波E，和E，具有不同振幅及不同相位，合成波失量的端点轨迹是一个椭圆，因此，这种平面波称为椭圆极化波4VEKEE,(=,t)_Emtana:[E(,)EbWUWE2E,E,cos@= sin?@EmEmEE

8-4. 平面波的极化特性 电场强度的方向随时间变化的规律称为电磁波的极化特性。 1.两个相互正交的线极化平面波Ex 及 Ey具有不同振幅，但具有相同的相位， 它们合成仍然是线极化波，反之，任一线极化波可以分解为两个相位相同或相 反的空间相互正交的线极化波。 2.两个线极化波Ex 及 Ey 的相位差为 ，但振幅皆为Em，合成波的电场强度 矢量的端点轨迹为一个圆，这种变化规律称为圆极化。当t 增加时，夹角不 断地减小，合成波矢量随着时间的旋转方向与传播方向ez 构成左旋关系，这 种圆极化波称为左旋圆极化波。 3.两个相互正交的线极化波Ex和 Ey 具有不同振幅及不同相位，合成波矢量的 端点轨迹是一个椭圆，因此，这种平面波称为椭圆极化波 2 π m m ( , ) ( , ) tan x y x y E E E z t E z t  = = z y x O  y x E x y ' ' Ey m Ex m   2 m m 2 m 2 m cos sin 2 ( ) + ( ) − = x y x y y y x x E E E E E E E E

在微波设备中，有些器件的功能就是利用了电磁波的极化特性获得的，例如，铁氧体环行器及隔离器等。众所周知，光波也是电磁波。但是光波不具有固定的极化特性，或者说，其极化特性是随机的。光学中将光波的极化称为偏振，因此，光波通常是无偏振的。为了获得偏振光必须采取特殊方法立体电影是利用两个相互垂直的偏振镜头从不同的角度拍摄的。因此，观众必须佩带一副左右相互垂直的偏振镜片，才能看到立体效果

众所周知，光波也是电磁波。但是光波不具有固定的极化特 性，或者说，其极化特性是随机的。光学中将光波的极化称为 偏振，因此，光波通常是无偏振的。 为了获得偏振光必须采取特殊方法。 立体电影是利用两个相互垂直的偏振镜头从不同的角度拍摄 的。因此，观众必须佩带一副左右相互垂直的偏振镜片，才能 看到立体效果。 在微波设备中，有些器件的功能就是利用了电磁波的极化特 性获得的，例如，铁氧体环行器及隔离器等

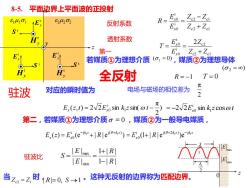
8-5.平面边界上平面波的正投射Ero1e2-ZR=o621202E反射系数EoZ, +ZelSr透射系数HExo2Zc2T=第EoZ +Z.E'tE:若媒质①为理想介质（1=0），媒质②为理想导体S..(α2 =8)HH全反射T=0R=-1元电场与磁场的相位差为对应的瞬时值为驻波2E,(z,t)=2V2E/o sin kizsin(0t-") =-2/2Exo sin kizcOS0t第二，若媒质①为理想介质。=0，媒质②为一般导电媒质E(2)=El0(e-ik=+|R[ej(0+k=) = Ero(I+|Rlej(+2ki=)e-k:[EImex1+|R]011S驻波比|Enin1-[R当Z=Z,时1R=0,S→1。这种无反射的边界称为匹配边界

8-5. 平面边界上平面波的正投射  111  222 z x y S t t Ex t Hy S r r Ex r Hy S i i Ex i Hy 反射系数 透射系数 c2 c1 c2 c1 i 0 r 0 Z Z Z Z E E R x x + − = = c2 c1 c2 i 0 t 0 2 Z Z Z E E T x x + = = 全反射 若媒质①为理想介质 ( 1 = 0) ，媒质②为理想导体 ( )  2 =  R = −1 T = 0 驻波 对应的瞬时值为 ) 2 π ( , ) 2 2 sin sin( 1 i Ex z t = Ex0 k z  t − E k z t x 2 2 sin cos 1 i = − 0  电场与磁场的相位差为 2 π 第一 第二，若媒质①为理想介质 = 0 ，媒质②为一般导电媒质， ( ) (e | | e ) i j j( ) 0 1 1 k z k z Ex z Ex R − + = +  k z k z Ex R 1 1 i j( 2 ) j 0 (1 | | e )e + − = +  驻波比 1 | | 1 | | | | | | min max R R E E S − + = = 0  1 z 2 1 max E min E 当 时， 。这种无反射的边界称为匹配边界。 Zc2 = Z1 | R |= 0, S →1

多层边界上平面波的正投射6Zin(-I)-ZlR=-ZelZaZe3总反射系数Z.n(-l)+ZelE①②3Ze3 + jZ2 tan kezl输入波阻抗Zm(-1)=Zo2 2a+jzg tankal4EEt2Ex3天线罩消除边界反射，可在两种理想介质中间插入厚度为四分之一波长，输入波阻抗的方法是一种阻抗变换方法。利用四分之一波长夹层的阻抗变换作用消除了边界反射，达到匹配此外，如果该例中夹层媒质的相对介电常数等于相对磁导率即,=μ，那么，夹层媒质的波阻抗等于真空的波阻抗当这种夹层置于空气中，平面波向其表面正投射时，无论夹层的厚度如何，反射现象均不可能发生。换言之，这种媒质对于电磁波似平是完全“透明”的

6. 多层边界上平面波的正投射 Zc1 Zc2 Zc3 -l 0 z ① ② ③ + Ex1 + Ex3 − Ex2 + Ex2 − Ex1 总反射系数 in c1 in c1 ( ) ( ) Z l Z Z l Z R − + − − = Z Z k l Z Z k l Z l Z c2 c3 c2 c3 c2 c2 i n c2 j tan j tan ( ) + + 输入波阻抗 − = 消除边界反射，可在两种理想介质中间插入厚度为四分之一波长，输 入波阻抗的方法是一种阻抗变换方法。利用四分之一波长夹层的阻抗 变换作用消除了边界反射，达到匹配。 此外，如果该例中夹层媒质的相对介电常数等于相对磁导率， 即  r =  r ，那么，夹层媒质的波阻抗等于真空的波阻抗。 当这种夹层置于空气中，平面波向其表面正投射时，无论夹 层的厚度如何，反射现象均不可能发生。换言之，这种媒质对于 电磁波似乎是完全“透明”的。 天线罩