《大学物理实验》课程教案讲义（上）第一章 测量与误差的基本知识

第一章测量与误差的基本知识测量与误差是一门专门的科学，深入研究它需要丰富的实验经验和厚实的数学基础。本章只介绍测量与误差、误差处理、有效数字、测量结果的不确定度评定等基本知识。这些知识不仅在每一个物理实验中都要用到，而且是今后从事科学实验工作所必须了解和掌握的。第一节测量与误差1.1测量及其分类物理实验离不开对物理量进行测量，测量可归纳为直接测量和间接测量两类。直接测量：凡使用仪器和量具直接测得（读出）被测量的数值，这类测量为直接测量，如用电流表测电流，用温度计测温度等。间接测量：有些物理量常常需要根据一些理论公式，用直接测量的数据计算出被测物理量，这样的测量为间接测量。如对一段导线上的电阻可以采用直接测出流过它的电流1和其两端的电压U，根据欧姆定律R=，计算出电阻R，R的/测量即为间接测量。测量有时根据需要可分为单次测量和多次测量，不同的测量，误差的估算不一样。对一个物理量的测量过程就是寻找这个量的客观实际值的过程，理论证明待测量的客观实际值（真值）需经过无穷次测量后取平均值方可找到。考虑到实验仪器、测量方法、环境和测量者等因素的限制，单纯追求增加测量次数去寻找真值是没有意义的，所以使用任何仪器的任何一次测量，其结果都与真值有差异，这种差异就叫误差。实验总是根据所要求的精确度来制定方案、选用仪器的。在一定的要求下，还1

第一章 测 与误 识 量 差的基本知 测量与误差是一门专门的科学，深入研究它需要丰富的实验经验和厚实的数学 基础。本章只介绍测量与误差、误差处理、有效数字、测量结果的不确定度评定等 基本知识。这些知识不仅在每一个物理实验中都要用到，而且是今后从事科学实验 工作所必须了解和掌握的。 第一节 测量与误差 1.1 测量及其分类 物理实验离不开对物理量进行测量，测量可归纳为直接测量和间接测量两类。 直接测量：凡使用仪器和量具直接测得(读出)被测量的数值，这类测量为直接 测量，如用电流表测电流，用温度计测温度等。 间接测量：有些物理量常常需要根据一些理论公式，用直接测量的数据计算出 被测物理量，这样的测量为间接测量。如对一段导线上的电阻可以采用直接测出流 过它的电流 I 和其 两端的电压U ，根据欧姆定律 I U R = ，计算出电阻 R ，R 的 测量即为间接测量。 测量有时根据需要可分为单次测量和多次测量，不同的测量，误差的估算不一 样。 对一个物理量的测量过程就是寻找这个量的客观实际值的过程，理论证明待测 量的客观实际值(真值)需经过无穷次测量后取平均值方可找到。考虑到实验仪器、 测量方法、环境和测量者等因素的限制，单纯追求增加测量次数去寻找真值是没有 意义的，所以使用任何仪器的任何一次测量，其结果都与真值有差异，这种差异就 叫误差。 实验总是根据所要求的精确度来制定方案、选用仪器的。在一定的要求下，还 1

要以最小的代价来取得最好的结果，不能要求仪器越高级越好，环境条件（如恒温、恒湿）越稳定越好，测量次数越多越好等等，这样要求是不切实际或是浪费的。测量结果的误差是各个因素所引起的误差的总和。减少某些因素所引起的误差，可能代价较小；而减小另一些因素所引起的误差，所需的代价可能很大。为了提高测量的精确程度，往往是着力于减小某一两项主要的误差，于是，就要根据要求和误差的考虑进行合理的设计以及选择实验方案和仪器。实验的精华就在于此。1.2误差的基本知识前已讲述，在任何测量中，由于各种原因，测量值与客观实际值（称为真值）之间总是存在着差异。我们把测量值x与真值x。之差就称为测量值的绝对误差（简称误差）。记为4x(1-1-1)Ax'= x-x误差存在于一切测量之中，而且贯穿测量过程始终。使用任何一种仪器，进行任何一次测量，都会引起误差。测量所根据的方法和理论越繁多，所用的仪器装置越复杂经历的时间越长，引进误差的机会可能性就越大。误差根据其性质分为两类：系统误差和偶然误差。1.2.1系统误差定义及分类系统误差是在同一被测量的多次测量过程中保持恒定或以可以预知变化的测量误差的分量.例如总是使测量结果向一个方向偏离，偏离数值是一定的或按一定规律变化的。它的来源有几个方面。①仪器误差：这是由于仪器本身的缺陷或没有按规定条件使用仪器而造成的。如仪器零点不准，放大器非线性，照相底板的收缩，在20℃标定的标准电阻在30℃下使用等。②理论（方法）误差：这是由于测量所依据的理论公式本身的近似性或实验条件不能达到理论公式所规定的要求及测量方法所带来的。如理论公式没有把散热考虑在内：1T=2元,Vg上的成立条件是没有把接线电阻和接触电阻考虑在内：单摆的周期公式摆角趋于零，这在实际是达不到的；还有用伏安法测电阻时电表内阻的影响是否考2

要以最小的代价来取得最好的结果，不能要求仪器越高级越好，环境条件(如恒温、 恒湿)越稳定越好，测量次数越多越好等等，这样要求是不切实际或是浪费的。测量 结果的误差是各个因素所引起的误差的总和。减少某些因素所引起的误差，可能代 价较小；而减小另一些因素所引起的误差，所需的代价可能很大。为了提高测量的 精确程度，往往是着力于减小某一两项主要的误差，于是，就要根据要求和误差的 考虑进行合理的设计以及选择实验方案和仪器。实验的精华就在于此。 1.2 误差的基本知识 前已讲述，在任何测量中，由于各种原因，测量值与客观实际值(称为真值)之 间总是存在着差异。我们把测量值 x 与真值 之差就称为测量值的绝对误差(简称误 差)。记为 0 x Δx′ 0 Δ ′ = − xxx (1-1-1) 误差存在于一切测量之中，而且贯穿测量过程始终。使用任何一种仪器，进行 任何一次 测量，都会引起误差。测量所根据的方法和理论越繁多，所用的仪器装置越复杂， 经历的时间越长，引进误差的机会可能性就越大。 误差根据其性质分为两类：系统误差和偶然误差。 1.2.1 系统误差定义及分类 系统误差是在同一被测量的多次测量过程中保持恒定或以可以预知变化的测量 误差的分量.例如总是使测量结果向一个方向偏离，偏离数值是一定的或按一定规律 变化的。它的来源有几个方面。 ①仪器误差：这是由于仪器本身的缺陷或没有按规定条件使用仪器而造成的。如仪 器零点不准，放大器非线性，照相底板的收缩，在 20℃标定的标准电阻在 30℃下使 用等。 ②理论(方法)误差：这是由于测量所依据的理论公式本身的近似性或实验条件不能 达到理论公式所规定的要求及测量方法所带来的。如理论公式没有把散热考虑在内； 没有把接线电阻和接触电阻考虑在内；单摆的周期公式 g l = 2T π 上的成立条件是 摆角趋于零，这在实际是达不到的；还有用伏安法测电阻时电表内阻的影响是否考 2

虑在内等都属此类。③个人误差：这是由于观测者本人的心理特点及习惯偏向造成的。如使用停表计时，有人停表过长，有人停表过短，并非态度不认真所至。系统误差是有定值的，如游标尺的零点不准；有些是积累性的，用受热膨胀的钢质米尺进行测量，其指示值就小于真实长度，误差值随着测量长度成比例增加；还有些呈周期性变化，如仪器的转动中心与刻度盘的几何中心不重合造成的偏心差就是一种周期性变化的系统误差。系统误差总是使测量结果偏大或者偏小，其特征是带有确定性。因此，多次测量求平均值并不能消除系统误差。解决的方案是只有找到系统误差产生的原因，才可以采取一定的方法去消除它的影响或对测量结果进行修正。在某些重要的精密实验中，对系统误差的分析处理基至对整个工作的科学意义和水平起决定作用。表1列出了常用仪器的技术条件和仪器误差限，供在测量不确定度时对系统误差作综合考虑。表1-1-1常用仪器的技术条件和仪器误差限量具（仪器）最小分度值仪器误差限米尺1mm4 =0. 5mm游标卡尺50分度0.02mm4夜=0.02mm20分度0.05mm4枚=0. 05mm螺旋测微计0.01mm4夜=0.005mm（千分尺）物理天平0.01g（天平感量）4=0.01g（取天平感量）1℃普通温度计4枚=0.5℃指针式电表4=准确度等级%X满量程（准确度等级）数字表4夜=a%×读数+ND注：a-误差相对项系数，如1、2数字。D-最后一单位读数。N-最后一单位读数的N倍。数字式仪表的仪器误差可简单地取所显示的稳定不变的数字最小显示量。4夜=最小显示量。1.2.2随机误差（偶然误差）及其分布规律①随机误差随机误差：相同条件下重复测量同一量，由于各种偶然因素的影响，使得测量值随机变化，这种因随机变化而引起的误差称为随机误差（偶然误差）。如读数的上下3

虑在内等都属此类。 ③个人误差：这是由于观测者本人的心理特点及习惯偏向造成的。如使用停表计时， 有人停表过长，有人停表过短，并非态度不认真所至。 系统误差是有定值的，如游标尺的零点不准；有些是积累性的，用受热膨胀的 钢质米尺进行测量，其指示值就小于真实长度，误差值随着测量长度成比例增加； 还有些呈周期性变化，如仪器的转动中心与刻度盘的几何中心不重合造成的偏心差 就是一种周期性变化的系统误差。 系统误差总是使测量结果偏大或者偏小，其特征是带有确定性。因此，多次测 量求平均值并不能消除系统误差。解决的方案是只有找到系统误差产生的原因，才 可以采取一定的方法去消除它的影响或对测量结果进行修正。在某些重要的精密实 验中，对系统误差的分析处理甚至对整个工作的科学意义和水平起决定作用。表 1 列出了常用仪器的技术条件和仪器误差限，供在测量不确定度时对系统误差作综合 考虑。 表 1-1-1 常用仪器的技术条件和仪器误差限 量具（仪器） 最小分度值 仪器误差限 米尺 1mm Δ仪 =0.5mm 游标卡尺 50 分度 20 分度 0.02mm 0.05mm Δ仪 =0.02mm Δ仪 =0.05mm 螺旋测微计 （千分尺） 0.01mm Δ仪 =0.005mm 物理天平 0.01g（天平感量） Δ仪 =0.01g（取天平感量） 普通温度计 1℃ Δ仪 =0.5℃ 指针式电表 （准确度等级） Δ仪 =准确度等级%×满量程 数字表 Δ仪 =a%×读数+ND 注：a-误差相对项系数，如 1、2. 数字。D-最后一单位读数。N-最后一单位读数的 N 倍。 数字式仪表的仪器误差可简单．．地取所显示的稳定不变的数字最小显示量。 Δ仪 =最小显示量。 1.2.2 随机误差(偶然误差)及其分布规律 ①随机误差 随机误差:相同条件下重复测量同一量，由于各种偶然因素的影响，使得测量值 随机变化，这种因随机变化而引起的误差称为随机误差(偶然误差)。如读数的上下 3

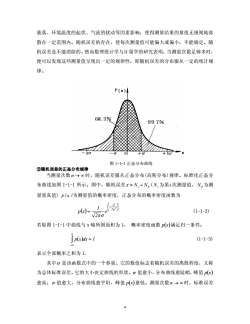
涨落、环境温度的起伏、气流的扰动等因素影响，使得测量结果的量值无规则地弥散在一定范围内。随机误差的存在，使每次测量值可能偏大或偏小，不能确定。随机误差是不能消除的。然而数理统计学与计量学的研究表明，当测量次数足够多时，便可以发现这些测量值呈现出一定的规律性，即随机误差的分布服从一定的统计规律。P(x)68.3%99.7%30olN-0+a+3g图1-1-1正态分布曲线②随机误差的正态分布规律当测量次数n8时，随机误差服从正态分布（高斯分布）规律。标准化正态分布曲线如图1-1-1所示。图中，随机误差x=N-N。（N为第i次测量值，N。为测量量真值）p（x）为测量值的概率密度，正态分布的概率密度函数为p(a)=一(-)(1-1-2)2元若取图1-1-1中曲线与x轴所围面积为1，概率密度函数p(x)满足归一条件：[ p(r)dx= 1(1-1-3)表示全部概率之和为1.其中。是该函数式中的一个参量。它的数值标志着随机误差的离散程度，又称为总体标准误差。它的大小决定曲线的形状。α值愈小，分布曲线愈陡，峰值p(x)愈高；α值愈大，分布曲线愈平坦，峰值p(x)愈低。测量次数n→时，标准误差4

涨落、环境温度的起伏、气流的扰动等因素影响，使得测量结果的量值无规则地弥 散在一定范围内。随机误差的存在，使每次测量值可能偏大或偏小，不能确定。随 机误差是不能消除的。然而数理统计学与计量学的研究表明，当测量次数足够多时， 便可以发现这些测量值呈现出一定的规律性，即随机误差的分布服从一定的统计规 律。 图 1-1-1 正态分布曲线 ②随机误差的正态分布规律 当测量次数 时，随机误差服从正态分布(高斯分布)规律。标准化正态分 布曲线如图 1-1-1 所示。图中，随机误差 n ∞→ = − NNx 0i ( 为第i 次测量值， 为测 量量真值) p( Ni N0 x )为测量值的概率密度，正态分布的概率密度函数为 ( ) ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = 2 2 2 x e 2 1 xp σ σπ (1-1-2) 若取图 1-1-1 中曲线与 x 轴所围面积为 1， 概率密度函数 (xp )满足归一条件： ( ) = 1dxxp ∫ ∞ ∞− (1-1-3) 表示全部概率之和为 1． 其中σ 是该函数式中的一个参量。它的数值标志着随机误差的离散程度，又称 为总体标准误差。它的大小决定曲线的形状。σ 值愈小，分布曲线愈陡峭，峰值 (xp ) 愈高；σ 值愈大，分布曲线愈平坦，峰值 (xp )愈低。测量次数n ∞→ 时，标准误差 4

定义为12xo(x)= lim,(1-1-4)n-→n从正态分布曲线可看出：测量值在随机误差x=0处出现的概率密度最大：误差较小的数据比误差较大的数据出现的概率大：绝对误差很大的数据出现的概率几乎等于零。③置信区间与置信概率如图1-1-1中阴影部分可算出P=p(x)x=68.3%，随机误差在（-α，+)区间概率为68.3%。P=zp(x)x=95.4%，随机误差在（-20，+20)区间概率为95.4%。P=p()dx=99.7%，随机误差在（-3g，+3α）区间概率为99.7%。在测量次数相当多的情况下，如果出现测量值误差的绝对值大于土3c的数据可以认为这是由于过失引起的异常数据，应加以剔除。但是，对于测量次数较少的情况，这种方法就不可靠，而需要采用另外的判别准则。说明：物理实验中常将3s（贝赛尔公式计算s，下面介绍）代替3c作为剔除实验数据中坏值的标准，称为误差极值。可以认为在测量次数n有限的情况下，对物理量的任一次测量值，其偏差大于3s，的可能性几乎不存在。如果某测量值N有N，-N≥3s，时，则需要考虑测量过程是否存在异常，并将该数据从实验结果中剔除。服从正态分布的随机误差有如下特征：单峰性：绝对值小的误差比绝对值大的误差出现的概率大。：对称性：绝对值相等的正误差和负误差出现的概率相等。。有界性：绝对值很大的误差出现的概率近于零。：抵偿性：随机误差的算术平均值随着测量次数的增加而趋近于零。当测量次数n→时，测量值的平均值可作为被测量真值的最佳估计，平均值趋近于真值。增加测量次数，可以减小偶然误差，这就是我们在实际工作中常常采取重复多次5

定义为 ( ) ∑= ∞→ = n 1i 2 i n x n 1 σ limx (1-1-4) 从正态分布曲线可看出：测量值在随机误差 = 0x 处出现的概率密度最大；误差 较小的数据比误差较大的数据出现的概率大；绝对误差很大的数据出现的概率几乎 等于零。 ③置信区间与置信概率 如图 1-1-1 中阴影部分可算出 = ( ) = %3.68dxxpP ∫ + − σ σ ，随机误差在( −σ ，+σ )区间概率为 68.3％。 ( ) %4.95dxxpP 2 2 = = ∫ + − σ σ ,随机误差在( − 2σ ，+ 2σ )区间概率为 95.4％。 ( ) %7.99dxxpP 3 3 = = ∫ + − σ σ ，随机误差在( − 3σ ，+ 3σ )区间概率为 99.7％。 在测量次数相当多的情况下，如果出现测量值误差的绝对值大于± 3σ 的数据可 以认为这是由于过失引起的异常数据，应加以剔除。但是，对于测量次数较少的情 况，这种方法就不可靠，而需要采用另外的判别准则。 说明:物理实验中常将 s3 x (贝赛尔公式计算 s x 下面介绍)代替3σ 作为剔除实 验数据中坏值的标准，称为误差极值。可以认为在测量次数 n 有限的情况下，对物 理量的任一次测量值，其偏差大于 s3 x 的可能性几乎不存在。如果某测量值 Ni 有 i x ≥− s3NN 时，则需要考虑测量过程是否存在异常，并将该数据从实验结果中剔 除。 ④服从正态分布的随机误差有如下特征 ．单峰性：绝对值小的误差比绝对值大的误差出现的概率大。 ．对称性：绝对值相等的正误差和负误差出现的概率相等。 ．有界性：绝对值很大的误差出现的概率近于零。 ．抵偿性：随机误差的算术平均值随着测量次数的增加而趋近于零。当测量次数 n ∞→ 时,测量值的平均值可作为被测量真值的最佳估计，平均值趋近于真值。 增加测量次数，可以减小偶然误差，这就是我们在实际工作中常常采取重复多次 5

测量的依据，但是，偶然误差是不能消除的。1.2.3标准偏差及其估算在实际测量中，测量次数Ⅱ总是有限的而且真值也不可知。因此标准误差只有理论上的价值。对标准误差的实际处理只能用标准偏差s.近似代替标准误差。进行估算。某一测量列的测量值分别为x，x2，x，实际测量估算时采用算数平均值示代替真值，常用贝赛尔公式计算s值，S，的表达式一之(,-对)st=n-i台(1-1-5)而n次测量的平均值的标准偏差为(1-1-6)r-xSI=Nn(n-11即一系列测量量的平均值标准偏差S是单次测量标准偏差s，的，/n总之：从以上分析误差的来源表明：测量结果的总误差是系统误差和偶然误差的总和。测量中应当限制或消除系统误差；正确地计算随机误差，并估算其范围；对测量结果给出正确、合适的评价

测量的依据，但是，偶然误差是不能消除的。 1.2.3 标准偏差及其估算 在实际测量中，测量次数 n 总是有限的而且真值也不可知。因此标准误差只有 理论上的价值。对标准误差σ 的实际处理只能用标准偏差 近似代替标准误差 x s σ 进 行估算。 某一测量列的测量值分别为 ， ，. ,实际测量估算时采用算数平均值 1 x 2 x n x x 代 替真值,常用贝赛尔公式计算 值， 的表达式 x s x s ∑( ) = − − = n 1i 2 x i xx 1n 1 s (1-1-5) 而 次测量的平均值的标准偏差为 n ( )∑( ) = − − = n 1i 2 x i xx 1nn 1 s （ 1-1-6 ） 即一系列测量量的平均值标准偏差 x s 是单次测量标准偏差 的x s n 1 。 总之：从以上分析误差的来源表明：测量结果的总误差是系统误差和偶然误差 的总和。测量中应当限制或消除系统误差；正确地计算随机误差，并估算其范围； 对测量结果给出正确、合适的评价。 6

第二节测量结果的不确定度评定20世纪80年代以来，不确定度表示体系经历了建立、完善和不断推广的过程。关于实验不确定度的表示的建议书（（RecommendationINC_1（198o）》发表后，冲击了以往的误差理论表示体系。1992年《测量不确定度表示法指南》的发表，使不确定度表示体系进人了一个日臻完善、全面推广的新阶段。1993年国际理论与应用物理联合会参与颁布了《指南》和《国际通用计量学基本术语》（第2版），说明推广不确定度表示是物理学研究和教学中的必然趋势2.1不确定度的概念不确定度是说明测量结果的一个参数，表征合理赋予被测量值的分散性。它表示由于测量误差的存在而对被测量值不能确定的程度。不确定度反映了可能存在的误差分布范围，即随机误差分量和未定系统误差分量的联合分布范围。它可近似理解为一定概率的误差限值，不确定度是在误差理论的基础上发展起来的。2.1.1误差与不确定度是两个不同的概念误差是一个理想的概念，根据传统的误差定义，由于真值一般是未知的，则测量误差一般也是未知的，是不能准确得知的。因此，一般无法表示测量结果的误差。不确定度则是表示由于测量误差的存在而对被测量值不能确定的程度，反映了可能存在的误差分布范围，表征被测量的真值所处的量值范围的评定，所以不确定度能更准确地用于测量结果的表示。一定置信概率的不确定度是可以计算出来（或评定）的，其值永远为正值。而误差可能为正，可能为负，也可能十分接近于零，而且一般是无法计算的。因此，可以看出误差和不确定度是两个不同的概念。2.1.2误差和不确定度是互相联系的误差和不确定度都是由测量过程的不完善引起的，而且不确定度概念和体系是在现代误差理论的基础上建立和发展起来的。在估算不确定度时，用到了描述误差分布的一些特征参量，因此两者不是割裂的，也不是对立的。普通物理实验中完整的测量结7

第二节 测量结果的不确定度评定 20 世纪 80 年代以来，不确定度表示体系经历了建立、完善和不断推广的过程。 关于实验不确定度的表示的建议书((Recommendation INC_1(1980)》发表后，冲击 了以往的误差理论表示体系。1992 年《测量不确定度表示法指南》的发表，使不确 定度表示体系进人了一个日臻完善、全面推广的新阶段。1993 年国际理论与应用物 理联合会参与颁布了《指南》和《国际通用计量学基本术语》(第 2 版)，说明推广 不确定度表示是物理学研究和教学中的必然趋势。 2.1 不确定度的概念 不确定度是说明测量结果的一个参数，表征合理赋予被测量值的分散性。它表 示由于测量误差的存在而对被测量值不能确定的程度。不确定度反映了可能存在的 误差分布范围，即随机误差分量和未定系统误差分量的联合分布范围。它可近似理 解为一定概率的误差限值，不确定度是在误差理论的基础上发展起来的。 2.1.1 误差与不确定度是两个不同的概念 误差是一个理想的概念，根据传统的误差定义，由于真值一般是未知的，则测 量误差一般也是未知的，是不能准确得知的。因此，一般无法表示测量结果的误差。 不确定度则是表示由于测量误差的存在而对被测量值不能确定的程度，反映了 可能存在的误差分布范围，表征被测量的真值所处的量值范围的评定，所以不确定 度能更准确地用于测量结果的表示。一定置信概率的不确定度是可以计算出来(或评 定)的，其值永远为正值。而误差可能为正，可能为负，也可能十分接近于零，而且 一般是无法计算的。因此，可以看出误差和不确定度是两个不同的概念。 2.1.2 误差和不确定度是互相联系的 误差和不确定度都是由测量过程的不完善引起的，而且不确定度概念和体系 是在现 代误差理论的基础上建立和发展起来的。在估算不确定度时，用到了描述误差分布 的一 些特征参量，因此两者不是割裂的，也不是对立的。普通物理实验中完整的测量结 7

果应给出被测量的量值x，同时还要标出测量的不确定度4，将实验结果写成x土△形式，这表示被测量量的真值在（x-4，x+）的范围以外的可能性很小。不确定度是指由于测量误差的存在而对被测量量值所处的量值范围的评定。2.2总不确定度4的估算方法测量结果的误差可能来自几个方面，其不确定度通常包含几个分量，我们可将这些分量分成A，B两类：A类分量指多次重复测量用统计方法估算的误差分量4.；B类分量指的是用其他方法估算的误差分量4它们可用“方和根”法合成，即测量结果的总不确定度为(1-2-1)A=1/42 +422.3直接测量的不确定度4的估算方法①不确定度A类分量4,的估算实际测量，只可能是有限次，此时测量误差不完全服从正态分布规律，而是服从所谓的t分布。此时A类分量不确定度4,由实验标准偏差s乘以因子(。/Vn)来求得(1-22)s为贝塞尔公式算出的标准偏差，t，是与测量次数n及置信概率p有关的量（称t，分布因子)。当概率P以及测量次数n确定后，t,也就确定了。当置信概率p=0.95时，（t，/Vn）的部分数据可以从表1-2-1查出。(a.s / n)分布值与测量次数关系表 1-2-1>测量次数n23456.89101520008.982. 481. 591.241. 050.930. 840. 720. 550. 470.1.96/-/(aos / Nn)物理实验中测量次数n一般不大于10，从表1看出，当5<n≤10时，（/n）近似值可取1(,//n~1),这时式(1-2-2)简化成(1-2-3)8

果应给出被测量的量值 x，同时还要标出测量的不确定度Δ，将实验结果写成 x±Δ 形式，这表示被测量量的真值在(x-Δ，x+ Δ)的范围以外的可能性很小。不确定度 是指由于测量误差的存在而对被测量量值所处的量值范围的评定。 2.2 总不确定度Δ的估算方法 测量结果的误差可能来自几个方面，其不确定度通常包含几个分量，我们可将 这些分量分成 A，B 两类： A 类分量指多次重复测量用统计方法估算的误差分量ΔA ； B 类分量指的是用其他方法估算的误差分量ΔB ； 它们可用“方和根”法合成，即测量结果的总不确定度为 (1-2-1) 2.3 直接测量的不确定度Δ的估算方法 2 2 Δ= Δ A B + Δ ①不确定度 A 类分量ΔA 的估算 实际测量，只可能是有限次，此时测量误差不完全服从正态分布规律，而是服 从所谓 的 t 分布。此时 A 类分量不确定度ΔA 由实验标准偏差 乘以因子 s ( nt ) p 来求得 s n t p A ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ Δ = (1-2-2) s为贝塞尔公式算出的标准偏差，p t 是与测量次数 n及置信概率 p有关的量（称 分布因子）。当概率 P 以及测量次数 确定后， 也就确定了。当置信概率 p=0.95 时， p t n p t ( nt ) p 的部分数据可以从表 1-2-1 查出。 表 1-2-1 ( nt ) 95.0 分布值与测量次数关系 测量次数 n 2 3 4 5 6 7 8 9 10 15 20 ∞ ( nt ) 95.0 8.98 2.48 1.59 1.24 1.05 0.93 0.84 O．77 0.72 0.55 0.47 96.1 ∞ 物理实验中测量次数 n 一般不大于 10，从表 1 看出，当 5< ≤10 时， n ( nt ) p 近似 值可取 1 ( 1nt ) p ≈ ,这时式(1-2-2)简化成 ss n t p A ≈ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ Δ = (1-2-3) 8

②测量的不确定度B类分量的估算B类分量的评定，有的依据仪器说明书，有的依据仪器的确定度等级，有的则粗略依据仪器分度值。普物实验中通常可取仪器的误差限值4作为B类分量，即(1-2-4)4g = 4仪③不确定度的合成4=4+4=/s+4袋(1-2-5)④相对不确定度的估算为了更全面地评定测量结果的优劣，还需考虑不确定度对测量值本身大小产生的相对的影响，为此，引入相对不确定度概念直观地评价测量结果的准确性，，其定义是4U，==×100%（百分数的形式）（1--2-6）x其中，△为合成不确定度，又为多次测量的平均值，U，为两者的比值称为测量的结果的相对不确定度。U.越小表示测量的准确性度逾高，测量结果准确：U.越大表示测量的准确性度逾低，则测量结果不准确。③测量结果完整表示正确地完成上述各步骤的计算，给出测量结果的完整表达式。完整的测量结果应给出被测量的最佳估计值，同时还要给出测量的合成不确定度，测量结果应写成如下标准形式：X=x±U,=α×100%X上述结果表示被测量量的真值落在区间反-4,x+△范围内的概率应在0.95以上，也就是说真值落在上述区间范围以外的概率极小。2.3.1单次测量不确定度的估算当实验中被测量量只测一次，此时4,分量不存在，可取总不确定度4=4：=4仪作

②测量的不确定度 B 类分量的估算 B 类分量的评定，有的依据仪器说明书，有的依据仪器的确定度等级，有的则 粗略依 据仪器分度值。普物实验中通常可取仪器的误差限值Δ仪 作为 B 类分量，即 ΔB = Δ仪 (1-2-4) ③不确定度的合成 2 22 B 2 A ΔΔΔ s +≈+= Δ仪 (1-2-5) ④相对不确定度的估算 为了更全面地评定测量结果的优劣，还需考虑不确定度对测量值本身大小产生 的相对的影响，为此，引入相对不确定度概念直观地评价测量结果的准确性，,其定 义是 %100 x Ur ×= Δ （百分数的形式）(1-2-6) 其中，Δ为合成不确定度，x 为多次测量的平均值， 为两者的比值称为测量 的结果的相对不确定度。 越小表示测量的准确性度逾高,测量结果准确; 越大表 示测量的准确性度逾低，则测量结果不准确。 Ur Ur Ur ⑤测量结果完整表示 正确地完成上述各步骤的计算，给出测量结果的完整表达式。完整的测量结果应 给出被测量的最佳估计值，同时还要给出测量的合成不确定度，测量结果应写成如 下标准形式： x x = ± Δ Ur 100% x Δ = × 上述结果表示被测量量的真值落在区间[ − Δ x,x + Δ]范围内的概率应在 0.95 以 上，也就是说真值落在上述区间范围以外的概率极小。 2.3.1 单次测量不确定度的估算 当实验中被测量量只测一次，此时ΔA 分量不存在，可取总不确定度Δ = ΔB = Δ仪 作 9

为单次测量不确定度的评定。仪器基本误差可以由仪器技术指标或有关手册查出也可以取最小刻度的一半作为仪器误差。（一般由实验室直接给出4值）。2.3.2直接测量量不确定度估算举例例：用螺旋测微计测某一钢丝的直径，6次测量值y分别为：0.249，0.250,0.247，0.251，0.253，0.250；同时读得螺旋测微计的零位y。为：0.004，单位mm，已知螺旋测微计的仪器误差为4=0.005mm，请给出完整的测量结果。解：测得值的最佳估计值为y= y- yo = 0.250 - 0.004 = 0.246(mm)贝塞尔公式计算标准偏差[E(-)（代入数据）=0.002mmS-n-1测量次数n=6，可近似有4=42+4=/s2+4双2=V0.002*+0.005*0.005mm则：测量结果为y=0.246±0.005mm3 U, =2.0%2.4间接测量木确定度的估算2.4.1间接测量不确定度的估算间接测量结果由直接测量数据依一定的数学公式计算出来。显然直接测量结果的不确定必然影响到间接测量结果，这种影响也可以由数学公式计算出来，设间接测量数学公式N=f(x,y,z,.)，其中x，y，z，是直接测量结果，它们之间相互独立。它们各自不确定度为4，4,，4.，便可得间接测量的不确定度计算式(1-2-7)4 = (%4) +(%4) (%4 +.或(1-28)和、差函数应用式（1-2-7)计算方便；积、商形式函数应用式(1-2-8)计算方便。10

为单次测量不确定度的评定。仪器基本误差可以由仪器技术指标或有关手册查出， 也可以取最小刻度的一半作为仪器误差。（一般由实验室直接给出Δ仪 值）。 2.3.2 直接测量量不确定度估算举例 例：用螺旋测微计测某一钢丝的直径，6 次测量值 分别为：0.249, 0.250, 0.247, 0.251, 0.253, 0.250; 同时读得螺旋测微计的零位 为：0.004, 单位 mm， 已知螺旋测微计的仪器误差为 i y 0 y Δ仪 =0.005mm，请给出完整的测量结果。 解：测得值的最佳估计值为 0.250 0.004 =−=−= 0.246(mm) 0 yyy 贝塞尔公式计算标准偏差 （代入数据） = 0.002mm − − = ∑ = 1 )(1 2 n yy s n i i 测量次数 n=6，可近似有 s 005.0005.0002.0 mm 2 2 2 2 2 B 2 A ΔΔΔ Δ仪 =+≈+= ≈+ 则：测量结果为 ±= mm005.0246.0y r = %0.2U 2.4 间接测量不确定度的估算 2.4.1 间接测量不确定度的估算 间接测量结果由直接测量数据依一定的数学公式计算出来。显然直接测量结果 的不 确定必然影响到间接测量结果，这种影响也可以由数学公式计算出来。 设间接测量数学公式 = ( ,z,y,xfN L)，其中 x ， ，y z ，.是直接测量结果，它 们之间相互独立。它们各自不确定度为Δx ，Δy ，Δz ，.便可得间接测量的不确定 度计算式 (1-2-7) ⎟ +L ⎠ ∂ ⎞⎛ ⎞⎛ 2 2 f ⎜ ⎝ ∂ ∂ + ⎟ ⎟ ⎠ ⎜ ⎜ ⎝ ∂ ⎟ + ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ = y z 2 N x zy f x f Δ Δ Δ Δ 或 (1-2-8) 和、差函数应用式(1-2-7)计算方便；积、商形式函数应用式(1-2-8)计算方便。 10