《电磁场与电磁能》课程PPT教学课件（马冰然版）第四章 恒定磁场

第贝章恒定磁场磁场是由运动电荷或电流产生的；当产生磁场的电流恒定时，它所产生的磁场不随时间变化，这种磁场称为恒定磁场

第四章 恒定磁场 磁场是由运动电荷或电流 产生的；当产生磁场的电 流恒定时，它所产生的磁 场不随时间变化，这种磁 场称为恒定磁场

第四章4.1恒定磁场的实验定律和磁感应强度与库仑定律相对应一、安培力定律：实验表明：通有恒定电流的回路之间有相互作用力dl先讨论真空中的情况：如图dl.P(x)R回路C中的任一电流元Ldl对回路2中的任一电流元12dlz的作用力为dFa, = Ho. I2dl, (I,dli ×ar)(4-1-1)R?4元02025/6/1

2025/6/11 第四章 2 4.1 恒定磁场的实验定律和磁感应强度 一 、安培力定律： 与库仑定律相对应 实验表明：通有恒定电流的回路之间有相互作用力。 先讨论真空中的情况：如图 2 I o 1 c 2 c 1 r  2 r  1 dl  2 dl  1 I R  回路 中的任一电流元 对回路 中的任一电流 元 的作用力为 1 c 2 c 1 1 I dl  2 2 I dl  2 0 2 2 1 1 21 ( ) 4 R I dl I dl a dF R       =    （4-1-1） P x y z ( , , )

第四章则回路C对回路 c2的作用力为：Fit = o ff ldl, x(ali xar)(4-1-2)R24元JJC2 Ci其中：=4元 ×10'H/ m —→真空中的磁导率。dl.根据牛顿第三定律：di,1RF21= -F12-3r2025/6/1130

2025/6/11 第四章 3 则回路 c1 对回路 c2 的作用力为：    = 2 1 2 0 2 2 1 1 2 1 ( ) 4 c c R R I dl I dl a F       （4-1-2） 其中： 4 10 H / m 7 0 −  =   真空中的磁导率。 根据牛顿第三定律： F21 F12   = − 2 I o 1 c 2 c 1 r  2 r  1 dl  2 dl  1 I R 

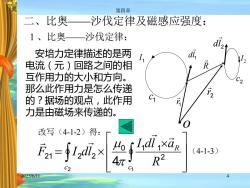
第四章二、比奥沙伐定律及磁感应强度：1、比奥-一沙伐定律：d安培力定律描述的是两di,LR电流（元）回路之间的相互作用力的大小和方向。那么此作用力是怎么传递2的？据场的观点，此作用力是由磁场来传递的。0改写（4-1-2）得：Ho s Liali xarF21 = f I 2dli, ×(4-1-3)R?4元C1C22025/6/11

2025/6/11 第四章 4 二、比奥——沙伐定律及磁感应强度： 1 、比奥——沙伐定律： 安培力定律描述的是两 电流（元）回路之间的相 互作用力的大小和方向。 那么此作用力是怎么传递 的？据场的观点，此作用 力是由磁场来传递的。 改写（4-1-2）得：            =  2 1 2 0 1 1 21 2 2 4 c c R R I dl a F I dl       （4-1-3） o 1 c 2 c 1 r  2 r  1 dl  2 dl  1 I R  2 I

第四章B, = Ho f lidli ×ar则定义：(4-1-4)108R24元B,为电流回路C,在场点（r2）产生的磁感应强度，B,与dl及aR垂直，并符合右手螺旋关系。为区别场点（x,y,z）与源点（x',J",z'），将上式改写成dl,比奥沙伐定律dl.I di'xarB=oR?4元(4-1-5)2025/6/11

2025/6/11 第四章 5 则定义：   = 1 2 0 1 1 1 4 c R R I dl a B      （4-1-4） 为电流回路 在场点（ ）产生的磁 感应强度， 与 及 垂直，并符合右 手螺旋关系。 C1 B1  B1  2 r  1 dl  R a  为区别场点（ x, y,z ）与源点（ x  , y  ,z  ），将上式改写成：    = c R R I dl a B 2 0 4      （4-1-5） 2 I o 1 c 2 c 1 r  2 r  1 dl  2 dl  1 I R  108

第四章讨论比奥一沙伐定律：di'P(x,y,z)比奥一沙伐定律描述的R是线电流在其周围产生的磁感应强度。其中Idl头12回路c'的电流元，若产r生磁场的电流不是线电流而是体电流或面电流呢？0实验表明：我们只要将电流元由线电流元Idi'分别改写成体电流元jdv"或面电流元j,ds，比奥一一沙伐定律仍然适用。025/6/11

2025/6/11 第四章 6 讨论比奥——沙伐定律： 比奥——沙伐定律描述的 是线电流在其周围产生的 磁感应强度。其中 为 回路 的电流元，若产 生磁场的电流不是线电流， 而是体电流或面电流呢？ Idl   c  实验表明：我们只要将电流元由线电流元 分别改写成体电流元 或面电流元 ，比 奥——沙伐定律仍然适用。 Idl   JdV  Js dS  o c  1 r  2 r  dl   I R  P x y z ( , , )

第四章2、体电流在场点P(x,y,z）产生的磁感应强度为(xy,z)=[(xy)xaindv(4-1-6)R?4元2503、面电流在场点 P(x,y,z）产生的磁感应强度为B(xy,z)=(y)xands( 4-1-7)R?4元B的单位：T特（斯拉）=Wb/m2韦伯每平方米1T=10Gs2025/6/11

2025/6/11 第四章 7 2 、体电流在场点 P( x, y,z) 产生的磁感应强度为 dV R J x y z a B x y z V R      =   2 0 ( , , ) 4 ( , , )      dS R J x y z a B x y z s s R      =   2 0 ( , , ) 4 ( , , )      3 、面电流在场点 P( x, y,z) 产生的磁感应强度为 （4-1-6） （ 4-1-7 ） B  的单位： T特（斯拉）= Wb/㎡ 韦伯每平方米 T Gs 4 1 =10 25

第四章三、洛仑兹力：电流回路℃2在电流回路c的1、安培力：磁场中所受的磁场力为：F21 = f I2dli, ×B,C22、推论：某磁场B作用于任一电流元dl的力为：dF=Idi × B3、线电流：I=PV则 Idi = puvdli = dqv2025/6/11

2025/6/11 第四章 8 三、洛仑兹力： 1 、安培力：  =  2 21 2 2 1 C F I dl B    电流回路 在电流回路 的 磁场中所受的磁场力为： 1 c2 c 2 、推论： 某磁场 B 作用于任一电流元 的力为：  Idl  dF Idl B    =  3 、线电流： I = vlv 则 Idl vdl dqv vl    =  =

第四章4、元电荷dq所受的磁场力为：dF=dqv× B5、洛仑兹力：磁场B对以速度 运动的电荷 q的作用力为：F=qixB=q(vxB)F6、电场E与B同时存在，运动电荷9所受的力为：Fa-Fa+Ft=α(VxB+E)F语改变讠的方向，改变的大小。2025/6/11

2025/6/11 第四章 9 dF dqv B    =  4 、元电荷 dq 所受的磁场力为： 5 、洛仑兹力： 磁场 B 对以速度 运动的电荷 的作用力为：  v  q F qv B q( v B)      =  =  F v   ⊥ 6 、电场 E 与 同时存在，运动电荷 所受的力为：  B  q F F F q( v B E)       = + =  + 总 洛 电 改变 的方向， F电 改变 的大小。  洛 F  v  v 

第四章例1：计算长为2l、通有电流的细直导线外任意一点处的磁感应强度 BN0,P(r,0,z)1解：由比奥一沙伐定律：01dzsRaRB= Ho fI di'xarR?r4元O011选取坐标系一柱坐标系：将导线对称地置于z轴上。：源电流I与无关，则B与β也无关，为简单起见，选场点为P(r,0,z）。如图.: B(r,z) αc (dl'×ar)= B(r,z)a025/6/1110

2025/6/11 第四章 10 P(r,0,z) r r o l l z  dz   2   1 R a  R z 解：由比奥——沙伐定律： 例1：计算长为2 、通有电流I的细直导线外 任意一点处的磁感应强度 B 。  l    = c R R I dl a B 2 0 4      a B r z dl a B r z R     ∴ ( , )  (  )  ( , ) 选取坐标系——柱坐标系：将导线 对称地置于 z 轴上。 ∵ 源电流I与 无关，则 与 也无关，为简单 起见，选场点为 。如图 B   P(r,0,z)