西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第一章 静电场

第一章 静电场 序 电场强度 静电场环路定律、高斯定律 静电场基本方程、分界面上的衔接条件 静电场边值问题、唯一性定理 分离变量法 有限差分法 ○○○○○ 镜像法和电轴法 电容和部分电容 静电能量与力
第一章 静电场

合D第一章静电场●静电场:相对观察者静止且量值不随时间变化的电荷所产生的电场。。本章任务:阐述静电荷与电场之间的关系,在已知电荷或电位的情况下求解电场的各种计算方法,或者反之。静电场知识结构框图·静电场是本课程的基础。由此建立的物理概念、分析方法在一定条件下可类比推广到恒定电场,恒定磁场及时变场
第一章 静 电 场 • 静电场: 相对观察者静止且量值不随时间变化的电荷所产生的电场。 • 本章任务: 阐述静电荷与电场之间的关系,在已知电荷或电位的情况下求解 电场的各种计算方法,或者反之。 • 静电场是本课程的基础。由此建立的物理概念、分析方法在一 定条件下可类比推广到恒定电场,恒定磁场及时变场。 • 静电场知识结构框图

合KD1.1.电场强度1.1.1 库仑定律库仑定律是静电现象的基本实验定律。大量试验表明:真空中两个静止的点电荷1与92之间的相互作用力:9192.E12F2, = N(牛顿)O4元0R2R9Fiz2 = 9192. E21N(牛顿)4元R2F2, = -F12图1.1.1两点电荷间的作用力适用条件·两个可视为点电荷的带电体之间相互作用力;10-9·无限大真空情况(式中80=8.85×10-l2F/m)36元*可推广到无限大各向同性均匀介质中(→)思考当真空中引入第三个点电荷9:时,试问,与92相互间的作用力改变吗?为什么?结论:电场力符合失量叠加原理
1.1.1 库仑定律 1.1 电场强度 2 12 0 1 2 21 4 R q q e F = N( 牛顿) F21 = −F12 适用条件 • 两个可视为点电荷的带电体之间相互作用力; • 无限大真空情况 (式中 可推广到无限大各向同性均匀介质中 12 9 8.85 10 36 10 − − = = 0 F/m) ( ) 0 → 2 21 0 1 2 12 4 R q q e F = N( 牛顿) 结论:电场力符合矢量叠加原理 图1.1.1 两点电荷间的作用力 库仑定律是静电现象的基本实验定律。大量试验表明: 真空中两个静止 的点电荷 q1 与 q2 之间的相互作用力: 当真空中引入第三个点电荷 时,试问 与 相互间的作用力改 变吗? 为什么? 3 q 1 q 2 q

AKKD112请静电场基本物理量电场强度F(X,y,=)定义: E(x,y,=)=limV/m (N/C)qi90电场强度(Electric Field Intensity)E表示单位正电荷在电场中所受至的力(F),它是空间坐标的失量函数,定义式给出了E的大小、方向与单位。a)点电荷产生的电场强度ZAFqeEp(r):V/m4neoze,qtFqr-rqyE,(r)=q480r-r-rq(r)q(r-r')-I=RZ4元80r-r个p(r)qy4TE,REeRV/m图1.1.2点电荷的电场
1.1.2 静电场基本物理量——电场强度 定义: q 0 qt ( x, y,z ) ( x, y,z ) lim t F E → = V/m (N/C) 电场强度(Electric Field Intensity ) E 表示单位正电荷在电场中所受到 的力(F ), 它是空间坐标的矢量函数, 定义式给出了E 的大小、方向与单位。 a) 点电荷产生的电场强度 2 r t 0 p 4 r q q ( ) e F E r = = V/m ' ' 4 ' q q ( ) 2 0 t p r r r r r r F E r − − − = = 3 0 4 ' q( ' ) r r r r − − = 2 R 4 0 R q e = V/m 图1.1.2 点电荷的电场
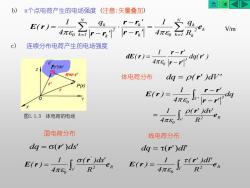
合KDb)n个点电荷产生的电场强度(注意:矢量叠加)1Nqkqkr-rE(r).eV/m4元8r-r'4元%Rkrc)连续分布电荷产生的电场强度1r-r'dE(r)dq(r')4元8-P(r)dvR=r-rdq = p(r' )dV'体电荷分布P(r)-E(r)do4元80rr1P(r')dy图1.1.3体电荷的电场eRR?4元80面电荷分布线电荷分布dq = o(r')ds'dq = t(r')dlo(r)ds'1t(r')dlE(r)E(r)eReRJR2R?4元4元8
b) n个点电荷产生的电场强度 (注意:矢量叠加) c) 连续分布电荷产生的电场强度 dq( ' ) ' ' 4 1 ( ) 3 0 r r r r r dE r − − = k N k 1 2 k k k 0 k N k 1 2 k k 0 R q 4 1 ' ' ' q 4 1 ( ) e r r r r r r E r = = = − − − = V/m 体电荷分布 dq = (r' )dV' dq ' ' 4 1 ( ) V' 3 0 − − = r r r r E r R v' 2 0 R ( ' )dv' 4 1 e r = 面电荷分布 R s' 2 ' 0 R ( )ds' 4 1 ( ) e r E r = dq = (r')ds' 线电荷分布 R l 2 0 ' R ( ' )dl' 4 1 ( ) e r E r = dq = (r')dl' 图1.1.3 体电荷的电场
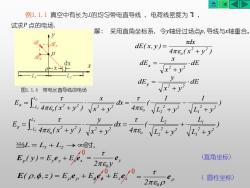
AKKD例1.1.1真空中有长为L的均匀带电直导线,电荷线密度为丁,试求P点的电场解:采用直角坐标系,令y轴经过场点p,导线与x轴重合。tdxadE,dE(x, y) :4元8(x+y)UxdEdEdxX0X-上Vx+-L,L.ydEdE.X2+图1.1.4带电长直导线的电场11Tx2EL4元(x+)4元8Vx?+L+JL,+y2L,L,yE4元8(+)4元80+V+V当L=L+L,>8时,10(直角坐标)E,(y)=E,e, +Ele2元80TE(p,d,z)=E.e。+E(圆柱坐标)2元60P
例1.1.1 真空中有长为L的均匀带电直导线 , 电荷线密度为 , 试求P 点的电场. 解: 采用直角坐标系, 令y轴经过场点p,导线与x轴重合。 4 ( x y ) dx dE( x, y ) 2 2 o + = dE x y x dE 2 2 + x = dE x y y dE 2 2 + y = ) L y 1 L y 1 ( 4 dx x y x 4 ( x y ) E 2 2 1 2 2 2 o 2 2 L L 2 2 o 2 1 + − + = + + = − x ) L y L L y L ( 4 dx x y y 4 ( x y ) E 2 2 1 1 2 2 2 2 o 2 2 L L 2 2 o 2 1 + + + = + + = − y 当 = + →时, L L1 L2 p Ey y Ex x E ( y ) = e + e (直角坐标) y 0 2 y e = E E Ez z E( , ,z ) = e + e + e ( 圆柱坐标) e 2 0 = 图1.1.4 带电长直导线的电场

合KKD讨论与引伸无限长直均匀带电导线产生的电场为平行平面场。电场强度E(x,y,z)的矢量积分一般先转化为标量积分,然后再合成,即E=Eex+Ee+Ee·积分是对源点(x,y",z)进行的,计算结果是场点(x,y,z)的函数。点电荷的数学模型点电荷是电荷体分布的极限情况,可以把它看成是一个体积很小,电荷密度很大,总电量不变的带电小球体。当α一0时,电荷密度趋近于无穷大,通常IZ用冲击函数s表示点电荷的密度分布。N(xy.z)r0当r0S(x,y,z)=(r)=8当r=009.. S(x, y,z)dV'= (..8(r )dV'= 1(积分区域V包含r=0点)图1.1.5单位点电荷的密度分布点电荷的密度p(r)=q(r)
• 无限长直均匀带电导线产生的电场为平行平面场。 • 电场强度 E( x, y,z ) 的矢量积分一般先转化为标量积分, 然后再合成,即 E = Ex ex + Ey ey + Ez ez • 点电荷的数学模型 • 积分是对源点 (x' , y' ,z') 进行的,计算结果是场点 (x, y,z) 的函数。 点电荷是电荷体分布的极限情况,可以把它看成是一个体积很小,电荷密度 很大,总电量不变的带电小球体。 当 时,电荷密度趋近于无穷大,通常 用冲击函数 表示点电荷的密度分布。 a →0 ( x, y,z ) = (r ) = 当r 0 当r = 0 0 ( x, y,z)dV' (r)dV' 1 V' V' = = (积分区域V'包含r =0点) 图1.1.5 单位点电荷的密度分布 点电荷的密度 (r ) = q(r )

AKKD1.2静电场环路定律和高斯定律1.2.1静电场环路定律1.静电场旋度a点电荷E(r)=4元80[r-rr-rq_xV×E(r)=r-r134元80V×CF=CV×F+VCxF量恒等式r-r'1Vx-Vx(r-r)+vr-rr-r-rVx(r-r')=0直接微分得1x(r-r)=-3r-)Ax(r-r)=0r-rr-rl故V×E()=0电场强度E的旋度等于零
点 电 荷 3 0 ' ' 4 q ( ) r r r r E r − − = 3 0 ' ' 4 q ( ) r r r r E r − − = 矢量恒等式 CF =CF +CF ( ' ) ' 1 ( ' ) ' 1 ' ' 3 3 3 r r r r r r r r r r r r − − − + − = − − 直接微分得 (r − r' ) = 0 ( ' ) 0 ' ' ( ' ) 3 ' 1 3 3 − = − − − = − − r r r r r r r r r r 故 E(r ) 0 电场强度E 的旋度等于零 1.2 静电场环路定律和高斯定律 1. 静电场旋度 1.2.1 静电场环路定律

合KKD可以证明,上述结论适用于点电荷群和连续分布电荷产生的电场。即任一分布形式的静电荷产生的电场的旋度恒等于零,即VxE=-0表明静电场是一个无旋场2.静电场的环路定律由斯托克斯定理,得E.dl=9(V×E)·ds=0在静电场中,电场强度沿着闭合回路的环量恒等于零。。电场力作功与路径无关,静电场是保守场E·dl=0二者等价。V×E=0无旋场一定是保守场,保守场一定是无旋场
• 可以证明,上述结论适用于点电荷群和连续分布电荷产生的电场。 表明 静电场是一个无旋场。 即任一分布形式的静电荷产生的电场的旋度恒等于零,即 E = 0 2. 静电场的环路定律 • 在静电场中,电场强度沿着闭合回路的环量恒等于零。 • 电场力作功与路径无关,静电场是保守场。 无旋场一定是保守场,保守场一定是无旋场。 = l s E dl ( E ) ds 0 由斯托克斯定理,得 • = = l E 0 E dl 0 二者等价

AKD3电位函数1)电位的引出:V×E=0,根据量恒等式×Vβ=0E=-V在静电场中可通过求解电位函数(Potential),再利用上式可方便地求得电场强度E。式中负号表示电场强度的方向从高电位指向低电位。2)已知电荷分布,求电位以点电荷为例推导电位qr-r点电荷群E(r)= -4元%r-1qip(r):+4元%=-1r-r'r-rlIr-rl连续分布电荷q:. E(r)=-V1dq-Vpr)p(r)=O4元r-r4元8r-rq. p(r)=+Ctdldq: pdV, odS,4元r-
3 . 电位函数 E = − 在静电场中可通过求解电位函数(Potential), 再利用上式可方便地求得 电场强度E 。式中负号表示电场强度的方向从高电位指向低电位。 2) 已知电荷分布,求电位: 3 0 ' ' 4 q ( ) r r r r E r − − = C ' q 4 1 (r ) N i 1 i i 0 + − = = r r 点电荷群 C ' dq 4 1 (r ) v' 0 + − = r r 连续分布电荷 1) 电位的引出 以点电荷为例推导电位: 3 ' ' ' 1 r r r r r r − − = − − (r ) 4 ' q ( ) 0 = − − = − r r E r C 4 ' q (r ) 0 + − = r r E = 0, 根据矢量恒等式 = 0 dq : dV , dS, dl
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第二章 恒定电场.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第三章 恒定磁场.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第四章 时变电磁场.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第六章 平面电磁波的传播.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第五章 准静态静电场.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第七章 均匀传输导线中的导行电磁波.ppt
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第1章 自由空间中的麦克斯韦积分定律.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)目录.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第5章 根据边值观点的电准静态场.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第2章 自由空间中的麦克斯韦微分定律.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第6章 极化.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第3章 准静电学与准静磁学导言.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第4章 电准静态场 重叠积分观点.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第7章 传导与电准静态的电荷弛豫.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第9章 磁化.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第8章 磁准静态场 重叠积分和边值观点.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第10章 磁准静态弛豫和扩散.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第11章 能量 功率流和力.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第14章 一维波动力学.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第12章 电动力学场 重叠积分观点.pdf
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第六章 时变电磁场.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)总结复习.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第七章 平面电磁波.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)复习题题.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第五章 静态场的边值问题.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第三章 恒定电场.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.10 静电场能量、静电力.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.9 导体系统的电容.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.7 唯一性定理.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第四章 恒定磁场.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.6 分界面上的边界条件.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.8 镜像法.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.5 泊松方程和拉普拉斯方程.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.4 高斯通量定理.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.3 静电 场中的导体与电介质.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.1 库仑定律与电场强度 2.2 电位.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第一章 矢量分析.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第一章 矢量分析.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第二章 静电场.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第三章 静电场的边值问题.ppt
